Goede dag,

Uit de volgende opgave kom ik niet:



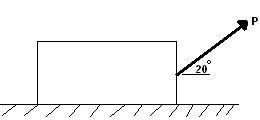
De kist heeft een massa van 80 kg en wordt met een ketting onder een hoek van 20 graden ten opzichte van de horizontale voortgetrokken. Bepaal de beginversnelling van de kist als de grootte van T opgevoerd wordt tot het krat begint te glijden, als de statische wrijvingscoëfficiënt μs = 0,5 is en de kinetische wrijvingscoëfficiënt μk = 0,3 is.

Wat ik doe:

Som van de verticale krachten = m ay => N - (80 · 9,81) + P sin20 = 0

Som van de horizontale krachten = m ax => P cos20 - 0,3N = 80 Ax

Ik neem aan dat ik nu P moet bepalen doormiddel van de statische wrijvingscoëfficiënt, maar ik zou niet weten hoe...

Alvast bedankt!

Je moet eerst uitrekenen hoe groot P moet zijn om de kist in beweging te brengen (d.w.z. de statische wrijving overwinnen).
dus dus 2 vergelijkingen met twee onbekenden, dus op te lossen (bijvoorbeeld N in 1 van de vergelijkingen isoleren en dan invullen in de andere vergelijking). De kracht P die hier uit rolt is de kracht die nodig is om de massa nét niet in beweging te laten komen, maar als hij ook maar een duizendste Newton groter is, dan zal de kist wel in beweging komen. Daarom rekenen we door met deze kracht P.

Nu heb je de kracht P en normaalkracht N. Zodra de massa in beweging komt, dan neemt de wrijving af, want de kinetische wrijving is kleiner dan de statische wrijving. Nu bereken je de versnelling door de tweede wet van Newton in te vullen in horizontale richting:
dus Hier is de versnelling uit te halen.