2 van 6
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 13:19
door Xilvo
Het volume is \(\frac{1}{12} \pi d^2(d+h)=\frac{1}{12} \pi d^3(1+1/dh)\) met \(dh=\frac{d}{h}\)
Dat volume moet je constant houden, de verhouding tussen volume en oppervlak is geen dimensieloze grootheid.
Dan kun je kiezen voor \(d=\left( \frac{1}{1+1/dh)} \right)^\frac{1}{3}\) en \(h=\frac{d}{dh}\)
Bij gegeven \(dh\) kun je dan \(d\) en \(h\) bepalen en kijken voor welke waarde van \(dh\) het oppervlak \(d+\sqrt{\frac{d^2}{4}+h^2}\) (constantes weggelaten) minimaal is.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 13:22
door wnvl1
HansH schreef: ↑za 14 sep 2024, 13:14
ja dat kan wel. moet alleen even uitzoeken hoe. ik kan wel snel een 2d plot maken met h/d op de horizontale as en d als parameter. is dat ook goed? kijk ik dan vanavond even naar.
Ik zal later zelf eens proberen of het gemakkelijk lukt in python om zoiets 3D te plotten.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 13:22
door HansH
maar ik had al even zitten experimenteren (helaas de source file weggegooid) maar voor elke d krijg ik dezelfde vorm dat oppervlak/volume het kleinst is voor zo groot mogelijke h. dat lijkt me ook logisch omdat oppervlak/volume van een kegel het kleinst is als de kegel nadert tot een cylinder (h->oneindig geeft A/V=d/4) en het grootst (zelfs oneindig) is als de kegel nadert tot een cirkel (h->0) wat het volume en oppervlak van de bol of een andere voorwerp is wat je eraan plakt maakt dan niet uit want dat verandert niet bij een bepaalde d.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 13:49
door Xilvo
HansH schreef: ↑za 14 sep 2024, 13:22
wat het volume en oppervlak van de bol of een andere voorwerp is wat je eraan plakt maakt dan niet uit want dat verandert niet bij een bepaalde d.
Ja, dat is wel van belang. Je moet uitgaan van een constant volume van het hele object, alleen dan krijg je een zinvol resultaat. De verhouding tussen oppervlak en inhoud is niet dimensieloos.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 14:02
door HansH
volgens mij geld voor elk object dat de verhouding tussen oppervlak en volume een functie is van de vorm en daarnaast nog schaalt met de diameter. bv voor een kubus geldt: V=r^3 an A=6r^2 dus de verhouding A/V is dan r/6
dus je kunt voor de ijsjesvorm gewoon d=1 nemen en dan de optimale h berekenen. dat levert dan een A/V waarde op die verhouding d/h is dan altijd het optimum, maar de verhouding A/V in dat optium is dan wel evenredig met d. Dus ik zou niet weten waarom je dan de bol mee moet nemen.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 15:45
door ukster
wnvl1 schreef: ↑za 14 sep 2024, 13:13
ukster schreef: ↑za 14 sep 2024, 12:56
How can?
Je zit met een hogere graadsvergelijking die ook oplossingen heeft die geen fysische betekenis. Maple zal er eentje uitpikken waarnaar ze convergeert. Fysisch heeft een negatieve complexe oplossing hier uiteraard geen betekenis.
ik heb alle oplossingen uit 'all values' onderzocht. de enige met fysische betekenis bleek d/h=1,7762 en dat is gelijk aan het eerder gegeven antwoord van Xilvo.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 15:46
door Xilvo
ukster schreef: ↑za 14 sep 2024, 12:56
How can?
Ik kom (met
\(x=1/\frac{d}{h}\)) op
\(x^4+6x^3+4x^2-3x-0,75=0\)
Daar voldoet mijn waarde aan (x=0,563, d/h=1,776) maar ook jouw waarde, d/h=-4,778 dus x=-0,2093.
Alleen zie ik niet hoe aan die waarde een betekenis te hechten.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 18:18
door RedCat
Bepaal A/V als functie f van d en h (d>0 anders degenereert de ijscone tot lijn):
\(\frac{A}{V} = \frac{\frac{1}{2}(4\pi r^2) + \pi r\sqrt{r^2+h^2}}{\frac{1}{2}\left(\frac{4}{3}\pi r^3\right)+\frac{1}{3}\pi r^2h}\)
\(= \frac{6\pi r^2 + 3\pi r\sqrt{r^2+h^2}}{2\pi r^3+\pi r^2h}\)
\(= \frac{6 + 3\cdot \sqrt{1+\frac{h^2}{r^2}}}{2r+h}\)
en dit levert de functie f(d,h):
\(f(d, h) = \frac{6 + 3\cdot \sqrt{1+4\frac{h^2}{d^2}}}{d+h}\)
met
\(f(d,0) = \frac{9}{d}\)
\(f(d,\infty) = \frac{6}{d}\)
Dan alleen nog aan te tonen dat er tussen nul en oneindig geen functiewaarde lager dan \(\small \frac{6}{d}\) is.
Noot:
\(f(1.776225,1) = 3.78852707...\)
maar
\(f(1.776225,2) = 3.54640838...\)
is kleiner dan dat.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 18:19
door HansH
wnvl1 schreef: ↑za 14 sep 2024, 13:09
Kan je in Mathcad of Maple geen mooie 3D plot maken van de verhouding van oppervlakte over volume in functie van h over d?
Dat gaat meer inzicht geven.
zoals ik al had een gegeven: de verhouding tussen oppervlak en volume van een willekeurig lichaam is een functie van de vorm en daarnaast nog schaalt met de diameter
ik heb nu in mathcad het oppervlak en volume uitgerekend van de kegel e van kegel+halve bol.
Daarna de verhouding oppervlak/volume als functie van d en h berekend en daarna die verhouding genormeerd met d.
na normering hou je dan nog 1 grafiek over die geldt voor alle d.
en uit die grafiek volgt dan weer dat oppervlak /volume steeds kleiner wordt bij toenemende h/d.
dus de kleinste verhouding tussen oppervlk en volume krijg je als h naar oneindig gaat.
- opp_vol
- (33.4 KiB) 22 keer gedownload
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 18:28
door HansH
RedCat schreef: ↑za 14 sep 2024, 18:18
en dit levert de functie f(d,h):
\(f(d, h) = \frac{6 + 3\cdot \sqrt{1+4\frac{h^2}{d^2}}}{d+h}\)
met
\(f(d,0) = \frac{9}{d}\)
\(f(d,\infty) = \frac{6}{d}\)
ik heb jouw fubctie erbij geplot in mathcad, maar levert niet dezelfde functie die ik heb.
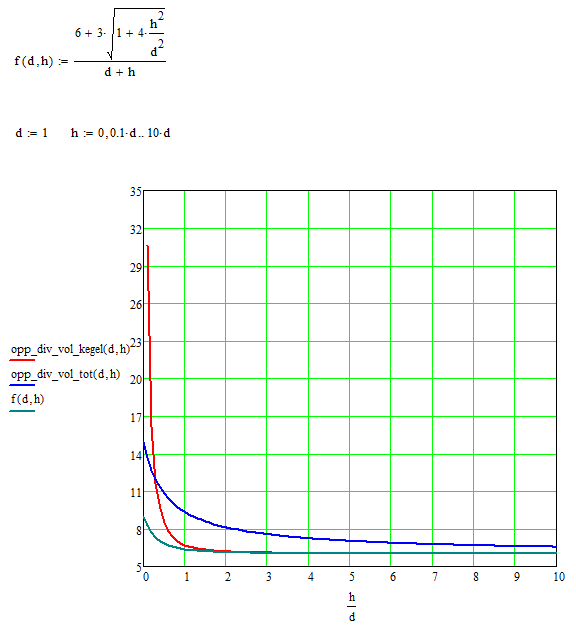
- av 566 keer bekeken
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 18:32
door Xilvo
RedCat schreef: ↑za 14 sep 2024, 18:18
Noot:
\(f(1.776225,1) = 3.78852707...\)
maar
\(f(1.776225,2) = 3.54640838...\)
is kleiner dan dat.
Bij de eerste set waardes is het volume 2,2931, bij de tweede set 3,1191.
Dus dan mag je niet (zonder meer) vergelijken.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 18:34
door HansH
sorry, foutje, ik had per ongeluk het oppervlak van de hele bol genomen ipv de halve bol.nu klopt het wel.
maar conclusie blijft hetzelfde:
de kleinste verhouding tussen oppervlk en volume krijg je als h naar oneindig gaat.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 18:47
door Xilvo
HansH schreef: ↑za 14 sep 2024, 18:34
sorry, foutje, ik had per ongeluk het oppervlak van de hele bol genomen ipv de halve bol.nu klopt het wel.
Mathcad - opp_inhoud.pdf
maar conclusie blijft hetzelfde:
de kleinste verhouding tussen oppervlk en volume krijg je als h naar oneindig gaat.
Dat is onjuist.
Als d/h=1,776225 en het volume is 1, dan wordt d=1,34697 h=0,75833 en het oppervlak wordt 4,99586
Als d/h=0,01 en het volume is 1, dan wordt d=0,33566 h=33,5663 en het oppervlak wordt 17,8753
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 19:27
door HansH
het maakt dus blijkbaar uit welke randvoorwaardes je hanteert.
jij neemt gelijkblijvend volume, ik neem gelijkblijvende d, maar je zou ook gelijkblijvend oppervlak kunnen nemen. blijkbaar krijg je in al die gevallen een verschillende uitkomst.
Re: verhouding d/h
Geplaatst: za 14 sep 2024, 19:39
door Xilvo
HansH schreef: ↑za 14 sep 2024, 19:27
het maakt dus blijkbaar uit welke randvoorwaardes je hanteert.
jij neemt gelijkblijvend volume, ik neem gelijkblijvende d, maar je zou ook gelijkblijvend oppervlak kunnen nemen. blijkbaar krijg je in al die gevallen een verschillende uitkomst.
Nee, je moet of volume of oppervlak gelijk houden. In beide gevallen levert dat hetzelfde resultaat.