[microcursus] warmtecapaciteit deel 1 : basisbegrippen
Geplaatst: do 24 dec 2009, 18:45
Er is ook een volledig overzicht van alle cursussen, FAQ's en handleidingen.
Bij deze cursus zijn ook een aantal oefenopgaven gemaakt, deze vind je onder de cursus.
Als je van deze cursus gebruik maakt, willen we je vriendelijk vragen te laten weten wat je er van vond:
---------------------------------------------------------------------------------------
[microcursus] WARMTECAPACITEIT deel 1 : basisbegrippen
Trefwoorden: calorimeter, joulemeter, calorimetrie, warmteberekening, energiebalans, warmtestroom, warmtebalans, temperatuur, warmtecapaciteit, soortelijke warmte, latente warmte, smeltwarmte, verdampingswarmte
Auteur: Jan van de Velde
1: Inleiding
Deze tweedelige basiscursus over calorimetrie is bedoeld voor (middelbare school) leerlingen die moeite hebben met rekenwerk rond de calorimeter en energiebalansen. Een aantal begrippen zoals entropie, arbeid e.d. komen op dit niveau niet of nauwelijks aan de orde, en ook andere zaken worden gewoonlijk versimpeld. Zo ook hier. In het laatste hoofdstuk van deel 2 zetten we daar nog wat kanttekeningen bij. Verder letten we in deze cursus voor de duidelijkheid in het rekenwerk NIET op significante cijfers.
In dit deel I van de cursus bespreken we de basisbegrippen. Wat is temperatuur, wat is warmte, wat is warmtecapaciteit? We moeten op molecuulniveau kijken om dat te begrijpen. We kijken naar berekeningen als:
Misschien kun je wel overweg met dit soort sommetjes. We raden je ook dan tóch aan om dit deel 1 door te nemen. Want een paar kleine misverstandjes, of "slechte (reken)gewoontes" zijn meestal de reden dat je vastloopt in de wat ingewikkelder berekeningen.
Ook is het onmisbaar dat je formules kunt ómschrijven, bijvoorbeeld van v=s/t naar s=vxt.
Neem zonodig eerst de [microcursus] formules herschrijven / vergelijkingen oplossen door.
In deel 2: rekenbladmethodegaan we op basis van die kennis dan verder met:
Er zijn eigenlijk maar vijf zeer eenvoudige formules nodig (waarvan er drie sterk op elkaar lijken), die iedereen kan onthouden, en verder wat gegevens uit een tabellenboek en...... systematisch werken.
2: Eerst afleren?
Misschien is deze stof niet nieuw voor je, en mogelijk leerde je de formules:
met:
(dus met Tbegin en Teind in omgekeerde volgorde)
VERGEET ZE !!! . Je krijgt van ons een paar andere. Die lijken er veel op, maar scheppen minder verwarring.
Dan is er nog DE grote begripsverwarring: warmte geeft aan hoe warm iets is. Nee !!
3: Inwendige energie: beweging van moleculen
Neem een speeltuinschommel, en geef er een klein duwtje tegen: daardoor geef je de schommel een beetje energie, de schommel gaat een beetje heen en weer bewegen. Blijf duwtjes geven, of geef een grotere duw, en de schommel gaat steeds harder heen en weer bewegen.
Met moleculen werkt dat ook ongeveer zo, en die kunnen bovendien op allerlei manieren bewegen:
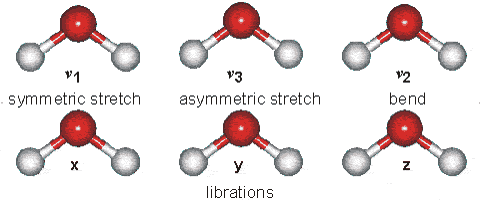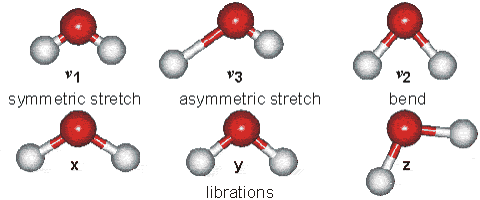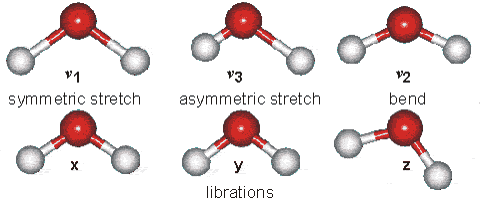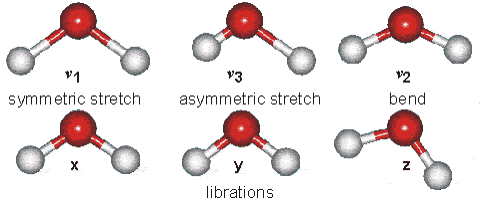 ...... (afb. 1) ...... London South Bank University
...... (afb. 1) ...... London South Bank University
(bewegingsmogelijkheden van een watermolecuul... artistieke impressie)
Bij het absolute nulpunt, 0 kelvin (-273,15 °C), staat alles stil. Gaan we dan energie toevoeren aan die stof, dan gaan de moleculen beetje bij beetje steeds heftiger bewegen. Andersom, haal energie uit de stof, en de moleculen gaan rustiger bewegen. Een blokje stof als geheel gaat hierdoor niet bewegen. Deze bewegingsenergie noemen we dan ook "inwendige energie".
Verder is er ook energie nodig als je de krachten tussen moleculen wil verkleinen, zodat ze ten opzichte van elkaar kunnen gaan bewegen (vaste stof wordt vloeistof). Ook dat zit in die "inwendige energie".
4: Wat is "temperatuur"?
[tr][td] Let op: omdat moleculen elkaar constant duwtjes geven is het onzin te spreken van de "temperatuur van een molecuul".
In de afbeelding kun je een animatie zien van moleculen in een gas. Een paar moleculen zijn rood gekleurd om beter te kunnen volgen. Door onderlinge botsingen verandert hun snelheid, en dus hun bewegingsenergie, voortdurend. De totale bewegingsenergie, en daardoor de gemiddelde bewegingsenergie per molecuul, verandert daarbij echter niet: [/td][td] ......(afb. 2)Wikipedia
......(afb. 2)Wikipedia
[/td][/tr]
[tr][td]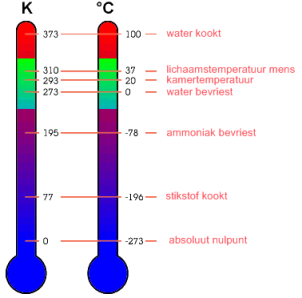
(afb. 3)bron: Planet-Terre
[/td][td]De grootheid temperatuur geven we aan met het symbool T, en de bijbehorende SI-eenheid is kelvin (K).
Bij 0 K is de gemiddelde bewegingsenergie van de moleculen 0 J. Alle moleculen staan dus stil.
Stiller dan stil kan niet. Daarom is 0 K het absolute nulpunt.
De kelvin en de graad Celsius zijn even grote eenheden, alleen het nulpunt ligt anders (zie afbeelding hiernaast).
Kelvin kun je daarom makkelijk omreken in graden Celsius met :
Het is een goede en vaak onmisbare gewoonte om met SI-eenheden, en hier dus o.a. met kelvin, te rekenen. Toch zul je ons hier vaak met °C zien rekenen. Voor uitleg waarom dat hier wel kan en mag zie de volgende paragraaf. [/td][/tr]
4.2 Verandering van temperatuur, ΔT
In calorimeterberekeningen hebben we zelden te maken met één temperatuur.
Het zal vrijwel altijd gaan om een begintemperatuur Tbegin, en dan gebeurt er iets met de energie, en krijg je een eindtemperatuur Teind.
We hebben te maken met een verandering van temperatuur.
Even iets zéér belangrijks over die
In de natuurkunde is het de vaste afspraak om "verandering van" (iets) áltijd te berekenen met :
Of het nu gaat over snelheid, plaats, temperatuur, volume, noem maar op. Correcte uitkomsten van berekeningen zijn altijd op deze afspraak gebaseerd.
Onze eerste formule is dan ook:
 NB: In de rest van deze cursus gebruiken we voor Tbegin en Teind vrijwel altijd zonder omrekenen de eenheid °C.
NB: In de rest van deze cursus gebruiken we voor Tbegin en Teind vrijwel altijd zonder omrekenen de eenheid °C.
Dat kan en mag in dit geval omdat we Tbegin en Teind alleen maar in verschilberekeningen gebruiken.
Bij zo'n berekening geeft 298 K - 277 K (= 21 K) immers precies hetzelfde resultaat als 25°C -4°C (= 21°C).
We zouden voor de netheid beter altijd de kelvin gebruiken. Dat heeft echter twee nadelen: de kans op omrekenfouten wordt groter, en temperaturen in kelvin zijn voor de meesten weinigzeggende getallen.
Voor ΔT, en in de eenheden voor warmtecapaciteit e.d. gebruiken we in deze cursus wél de kelvin.
Rekenvoorbeelden:
[tr][td]Een wegdek warmt op van -20°C naar +35°C. Wat is de verandering van temperatuur?
Tbegin = -20°C
Teind = +35°C
ΔT = ?? K
ΔT = Teind - T begin = 35 - (-20) = + 55 K[/td][td]Een radiator met een temperatuur van +85°C krijgt een verandering van temperatuur van -33 K. Wat wordt de eindtemperatuur?
Tbegin = +85°C
ΔT = -33 K
Teind = ?? °C
ΔT = Teind - T begin ==> Teind = ΔT + T begin = -33 + 85 = + 52°C [/td][/tr]
Ja, ΔT kan positief óf negatief zijn! Dit moeten we consequent volhouden. In formules waarmee we verderop gaan rekenen hebben die plussen of minnen grote invloed!!
We kunnen hetzelfde sommetje ook netjes in kelvin uitwerken.
Voor het eindresultaat heeft dat geen gevolgen, kijk maar in deze
5: Wat is "warmte"?
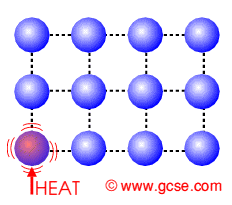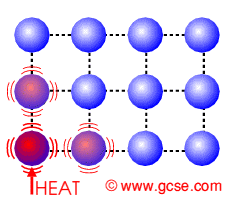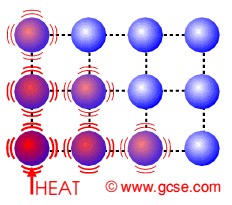
Als je energie toevoert aan een deel van een voorwerp, dan gaat een deel van de moleculen in dat voorwerp heftiger bewegen. Die geven daardoor ook duwtjes tegen hun buurmoleculen, die daardoor ook heftiger gaan bewegen. Dat heet dan geleiding. De energie verplaatst zich zo van een plaats met hoge temperatuur naar een plaats met lage temperatuur.
 ...... (afb. 4)......GCSE.com
...... (afb. 4)......GCSE.com
...... Geleiding van warmte in een vaste stof,
moleculen geven bewegingsenergie aan elkaar door)
Hou je op met energie toevoeren, dan krijgt na verloop van tijd het voorwerp overal dezelfde temperatuur. De moleculen bewegen dan allemaal gemiddeld even hard. Er is dan "thermisch evenwicht". Dat proces zal nooit spontaan omkeren, je zult de toegevoerde energie nooit meer spontaan ergens in een hoekje van je voorwerp samengebald terugvinden.
Dat geldt ook voor bijvoorbeeld een warm blokje metaal in koud water: even wachten en er ontstaat thermische evenwicht, blokje en water krijgen een gelijke temperatuur.
Daarmee komen we nu aan wat warmte WÉL is:
Behalve opwarmen kun je een voorwerp ook laten afkoelen: de moleculen van het voorwerp dragen dan hun energie over aan moleculen buiten het voorwerp, bijvoorbeeld een lepel hete soep warmt de lucht er rondom op, en wordt daardoor zelf kouder.
Oh, en nu we het er toch over hebben, "kou" bestaat niet in de natuurkunde. Als je je handen op een blok ijs legt stroomt er geen kou uit het ijs je handen in. Warmte stroomt uit je handen.
6: Warmtecapaciteit
Als je een hoeveelheid energie toevoert aan een voorwerp, zal de temperatuur van dat voorwerp veranderen. Als je twee keer zoveel energie toevoert, dan zal de temperatuur twee keer zo sterk veranderen.
Het ene voorwerp zal in temperatuur meestal meer of minder veranderen dan het andere voor eenzelfde hoeveelheid warmte. We kunnen dus spreken van de "warmtecapaciteit" van een voorwerp:
in formule:
Warmte (energie) druk je uit in joule, verandering van temperatuur in kelvin, warmtecapaciteit dus in joule per kelvin (J/K)
In warmteberekeningen gebruik je deze formule meestal in een iets andere vorm geschreven.
Dat geeft ons onze tweede formule:
Rekenvoorbeelden:
[tr][td]Om een blok marmer van 20°C in temperatuur te verhogen naar 35°C is 26 400 J warmte nodig. Wat is de warmtecapaciteit van het blok?
Tbegin = +20°C
Teind = +35°C
Q = 26 400 J
Cblok = ?? J/K
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 35 - 20 = +15 K
Q = C·ΔT dus Cblok= Q/ΔT = 26 400/15 = 1760 J/K
[/td][td]Een loden kogel met een warmtecapaciteit van 25 J/K koelt af van 300 naar 20°C. Hoeveel warmte wordt afgestaan aan de omgeving?
Tbegin = +300°C
Teind = +20°C
Ckogel = 25 J/K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 20 - 300 = -280 K
Q = C·ΔT = 25 x -280 = -7000 J [/td][/tr]
Ja, Q (de warmte) in het rechtse voorbeeld is negatief (omdat ΔT negatief was)! Blijkbaar betekent dat dat de warmte het voorwerp UITstroomt. Misschien even wennen.
 We zijn gewend om, heel economisch bekeken, dat wat we erin moeten stoppen als min te beschouwen (wij raken dat kwijt). In de natuur- en scheikunde doen we dat niet zo: we bekijken het vanuit de stof of het voorwerp. Dus:
We zijn gewend om, heel economisch bekeken, dat wat we erin moeten stoppen als min te beschouwen (wij raken dat kwijt). In de natuur- en scheikunde doen we dat niet zo: we bekijken het vanuit de stof of het voorwerp. Dus:
Reken consequent met die plusjes en minnetjes, en je berekeningen komen altijd uit.
7: Soortelijke warmtecapaciteit (soortelijke warmte)
In het vorige hoofdstuk hadden we het nog over een voorwerp, (een BLOK marmer, een loden KOGEL) en hoeveel warmte (energie) daar in moest om de temperatuur met 1 K te verhogen (de warmtecapaciteit). Het is natuurlijk logisch dat als dat voorwerp twee keer zo zwaar wordt, dat er dan ook twee keer zoveel warmte in of uit moet om dezelfde verandering van temperatuur te krijgen.
Iets minder voor de hand liggend is dat de warmtecapaciteit van een voorwerp óók afhangt van de soort stof waarvan het gemaakt is. De moleculen in een stof oefenen behoorlijke krachten op elkaar uit om bij elkaar te blijven, en de atomen in die moleculen ook. Naarmate die krachten groter zijn kost het meer energie om er beweging in te krijgen.
Een paar voorbeelden uit BINAS:
1 kg water heeft een warmtecapaciteit van 4180 J/K;
1 kg marmer heeft een warmtecapaciteit van 880 J/K;
1 kg lood heeft een warmtecapaciteit van 128 J/K;
Je ziet, dat scheelt nogal wat van stof tot stof.
In hoofdstuk 6 berekenden we de warmtecapaciteit van het blok marmer op 1760 J/K, het kostte 1760 joule om het blok 1 K in temperatuur te verhogen. Met de wetenschap dat het 880 joule kost om 1 kg marmer 1 K in temperatuur te doen stijgen, berekenen we al snel dat de massa van dat blok marmer 1760/880 = 2 kg geweest moet zijn.
in formule:
Iets anders geschreven leidt dat tot onze derde formule (die héél erg op de tweede lijkt):
Rekenvoorbeelden:
[tr][td]"We willen een halve liter water van 20°C opwarmen tot het kookpunt. Hoeveel warmte is er nodig?"
Tbegin = +20°C
Teind = +100°C
mwater= 0,5 kg (een halve liter water heeft een massa van 500 g)
cwater = 4180 J/kg·K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 100 - 20 = +80 K
Q = m·c·ΔT = 0,5 x 4180 x 80 = 167 200 J
[/td][td]Bij het afkoelen van een loden kogel van 300 naar 20°C wordt 7000 J warmte afgestaan aan de omgeving. Wat is de massa van de kogel?
Tbegin = +300°C
Teind = +20°C
clood = 128 J/kg·K
Q = -7000 J (minnetje! , want het voorwerp raakt warmte kwijt)
mlood = ?? kg
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 20 - 300 = -280 K
Q = m·c·ΔT dus m = Q/(c·ΔT) = -7000 : (128 x -280) = 0,195 kg [/td][/tr]
Niet onbelangrijk om te beseffen: een stof heeft in de verschillende fasen verschillende eigenschappen. Dat geldt zeker ook voor de stofeigenschap "soortelijke warmte". Bijvoorbeeld:
In berekeningen waarbij fasen veranderen kun je de verschillende fasen van één stof dus net zo goed als verschillende stoffen beschouwen.
8: Fase-overgangen: latente warmte
Moleculen in vaste stoffen oefenen forse krachten op elkaar uit. Ook in vloeistoffen zijn die krachten nog aanzienlijk. Een blokje ijzer, maar ook een waterdruppel, vallen niet zomaar uit elkaar. Er is heel wat energie nodig om de moleculen uit een vaste stof losser te maken tot een vloeistof, of uit een vloeistof geheel los te maken tot losse gasmoleculen.
 ......
......  (afb. 5)......Purdue University Dept. of Chemistry
(afb. 5)......Purdue University Dept. of Chemistry
(moleculen in een vloeistof resp. een gas... artistieke impressie)
Dat dat veel energie kost merk je goed als je een beetje zweet: voor het verdampen van dat beetje zweet wordt veel warmte aan je lichaam onttrokken. Ook zo als je water kookt: je blijft energie (warmte) toevoeren aan je pan op het fornuis, maar het water wordt niet warmer dan 100°C terwijl het vloeibare water in waterdamp van 100°C verandert.
in formule:
In warmteberekeningen gebruik je deze formule meestal in een iets andere vorm geschreven.
Dat geeft ons onze vierde formule (die heel erg op de tweede en derde lijkt) :
Rekenvoorbeelden:
[tr][td]In een koelbox met 3 kg ijsblokjes van 0°C "lekt" per uur 83 500 J aan warmte uit de omgeving binnen. Hoe lang duurt het voordat alle ijs gesmolten is?
m= 3 kg
Ls = 334 000 J/kg
Q = ?? J
Q= m·Ls = 3 x 334 000 = 1 002 000 J
t= 1 002 000 (J) / 83500 (J/h) = 12 h
[/td][td]Een loden kogel met een massa van 0,195 kg vraagt
4 875 J om te smelten. Wat is de smeltwarmte van lood?
Q= 4 875 J
m = 0,195 kg
Ls = ?? J/kg
Ls= Q/m = 4 875 / 0,195 = 25 000 J/kg
(en dat is een reële tabelwaarde) [/td][/tr]
Net als bij afkoelen en opwarmen geldt: er is evenveel energie nodig om 1 kg water te verdampen tot 1 kg damp, als dat er energie vrijkomt bij het condenseren van 1 kg damp tot 1 kg water. De condensatiewarmte (energie die vrijkomt als de damp weer terug condenseert) is dus even groot als de verdampingswarmte. Datzelfde geldt voor smelten en stollen, en natuurlijk ook voor sublimeren en rijpen.
Voor het verdampen van 1 kg water is 2 260 000 J energie nodig. Daarmee zou je 540 kg water 1 K kunnen opwarmen! Dit verschijnsel kun je nuttig gebruiken, want die energie krijg je weer terug als de damp weer condenseert. Mede daarom is stoom zo'n geliefd middel om energie te transporteren: per kg kun je er veel meer energie instoppen en weer terug uithalen dan uit heet water.
9: Wet van behoud van energie: som van de warmtestromen is nul
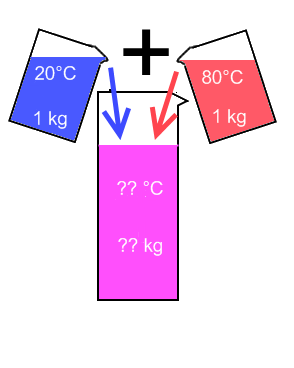
We voegen 1 kg water van 20°C samen met 1 kg water van 80°C. Wat wordt de eindtemperatuur?
.............................. (afb. 7)
(afb. 7)
Je hoeft geen genie te zijn om te snappen dat er in elk geval 2 kg water in die grote maatbeker terechtkomt. En een beetje snuggere basisschoolleerling zal al gauw vermoeden dat de eindtemperatuur in die grote beker 50°C zal zijn, het gemiddelde van die 20°C en die 80°C.
En zo blijkt zelfs een basisschoolleerling twee heel belangrijke natuurkundige gegevens eigenlijk al te kennen zonder die ooit geleerd te hebben:
1) Als er tussen twee stoffen een temperatuurverschil bestaat, ontstaat er een warmtestroom totdat beide stoffen een gelijke temperatuur hebben.
2) De energie die de ene stof daarbij afstaat is gelijk aan de energie die de andere stof opneemt.
Zoiets kun je op intuïtie nog wel oplossen. Tóch moeten we dit eens even netjes doen, want met intuïtie krijgen we het niet meer opgelost als we wat ingewikkelder gegevens krijgen (de opgaven zélf worden eigenlijk nooit ingewikkelder). Nu kunnen we alvast even oefenen.
We gaan er even van uit dat er geen warmte van binnen naar buiten gaat of andersom: dus, wat de ene stof aan warmte afstaat wordt door de andere stof opgenomen, de optelsom van die warmtestromen is gewoon 0.
Dit wordt dan gelijk de 5e en laatste formule die we nodig hebben:
Laten we eens zien of die 50°C klopt:
[tr][td] 1 kg water met een temperatuur van 20°C wordt opgewarmd tot 50°C. Hoeveel warmte is hiervoor nodig?
Tbegin = +20°C
Teind = +50°C
mwater= 1 kg
cwater = 4180 J/kg·K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 50 - 20 = +30 K
Q = m·c·ΔT = 1 x 4180 x 30 = 125 400 J
[/td][td]1 kg water met een temperatuur van 80°C wordt afgekoeld tot 50°C. Hoeveel warmte komt hierbij beschikbaar?
Tbegin = +80°C
Teind = +50°C
mwater= 1 kg
cwater = 4180 J/kg·K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 20 - 50 = -30 K
Q = m·c·ΔT = 1 x 4180 x -30 = -125 400 J
[/td][/tr][tr][td] check:
Qkoud water + Qwarm water = 125 400 + (-125 400) = 0[/td][/tr]
Samenvatting: Grootheden, eenheden, definities, formules
grootheid: MASSA ( m )
definitie: de hoeveelheid van een stof
SI-eenheid: kilogram (kg)
grootheid: TEMPERATUUR ( T )
definitie: een maat voor de bewegingsenergie van deeltjes in een hoeveelheid stof
SI-eenheid: kelvin (K) (we zullen hier overigens vaak met graden Celcius (°C) werken)
De eenheid K is overigens even groot als de eenheid °C. Alleen het nulpunt ligt anders:
0 K is dus - 273°C (eigenlijk -273,15°C, maar dat is niet zo belangrijk)
Nou zullen we in deze cursus vaak rekenen met verandering van temperatuur (ΔT) , (spreek uit: delta T). Omdat 1 K even groot is als 1°C maakt het dan weinig meer uit of we kelvin of graden Celsius gebruiken. Een ΔT van 21 K is een precies even grote verandering als een ΔT van 21°C.
grootheid: WARMTE ( Q )
definitie: Warmte is de energie die als gevolg van een temperatuurverschil door een warmtegeleidende wand stroomt. Warmte is een moeilijk begrip. (VERWAR HET NIET MET TEMPERATUUR!!) Warmte is een energiestroom. Je kunt dus niet spreken over 'de warmte' van een hoeveelheid stof. Geen paniek, je zult zien dat dit in de praktijk veel simpeler is dan het lijkt.
SI-eenheid: joule (J) (niet toevallig dezelfde als van energie)
grootheid: (voorwerps)WARMTECAPACITEIT ( C )
definitie: de hoeveelheid energie in joule die nodig is om een voorwerp één kelvin in temperatuur te laten stijgen. Deze is natuurlijk alleen voor precies dezelfde voorwerpen gelijk. Een groter voorwerp zal een grotere warmtecapaciteit hebben.
SI-eenheid: joule per kelvin (J/K) (de massa (kg) staat niet in deze formule: hij is vastgesteld voor het voorwerp, de massa is daar al in verrekend)
grootheid: SOORTELIJKE WARMTECAPACITEIT ( c )
definitie: de hoeveelheid energie in joule die nodig is om één kilogram van een stof één kelvin in temperatuur te laten stijgen. Deze is voor alle stoffen verschillend. Je kunt het voor de meeste stoffen in een tabellenboek vinden.
SI-eenheid: joule per kilogram per kelvin (J/kg·K) :
FASE: de toestand waarin een stof zich bevindt.
In deze cursus beperken we ons tot de drie belangrijkste fasen: vaste stof, vloeistof, gas (damp)
grootheid: LATENTE WARMTE ( L... ) (smelt-, stollings-, verdampings- en condensatiewarmte.)
definitie: de hoeveelheid energie in joule die nodig is (of die vrijkomt) bij het veranderen van de fase van een kilogram van een stof (bij gelijkblijvende temperatuur)dus bijvoorbeeld de warmte die nodig is om een kg ijs te laten smelten bij 0°C, of juist de warmte die vrijkomt als een kg water een kg ijs wordt.
SI-eenheid: joule per kilogram (J/kg) (de temperatuur (K) staat niet in deze formule: die verandert niet bij een fase-overgang: verdampen - condenseren - smelten - stollen)
1) Als er tussen twee stoffen een temperatuurverschil bestaat, ontstaat er een warmtestroom totdat beide stoffen een gelijke temperatuur hebben.
2) De energie die de ene stof daarbij afstaat is gelijk aan de energie die de andere stof opneemt.
 NB: kijk bij warmtestromen een beetje uit met plus en min. We zijn gewend om, heel economisch bekeken, dat wat we erin stoppen als min te beschouwen (wij raken dat kwijt). In de natuur- en scheikunde doen we dat niet zo: we bekijken het vanuit de stof of het voorwerp. Dus:
NB: kijk bij warmtestromen een beetje uit met plus en min. We zijn gewend om, heel economisch bekeken, dat wat we erin stoppen als min te beschouwen (wij raken dat kwijt). In de natuur- en scheikunde doen we dat niet zo: we bekijken het vanuit de stof of het voorwerp. Dus:
plus: de stof ontvangt energie. (of snelheid, of massa, of wat ook)
min: de stof staat energie af. (of snelheid, of massa of wat ook)
Bij deze cursus zijn ook een aantal oefenopgaven gemaakt, deze vind je onder de cursus.
Als je van deze cursus gebruik maakt, willen we je vriendelijk vragen te laten weten wat je er van vond:
- Geef eventuele foutjes aan;
- Zijn de onderdelen soms onduidelijk, of net erg helder?
- Ontbreken er volgens jou stukken, of heb je suggesties?
- ...
---------------------------------------------------------------------------------------
[microcursus] WARMTECAPACITEIT deel 1 : basisbegrippen
Trefwoorden: calorimeter, joulemeter, calorimetrie, warmteberekening, energiebalans, warmtestroom, warmtebalans, temperatuur, warmtecapaciteit, soortelijke warmte, latente warmte, smeltwarmte, verdampingswarmte
Auteur: Jan van de Velde
1: Inleiding
Deze tweedelige basiscursus over calorimetrie is bedoeld voor (middelbare school) leerlingen die moeite hebben met rekenwerk rond de calorimeter en energiebalansen. Een aantal begrippen zoals entropie, arbeid e.d. komen op dit niveau niet of nauwelijks aan de orde, en ook andere zaken worden gewoonlijk versimpeld. Zo ook hier. In het laatste hoofdstuk van deel 2 zetten we daar nog wat kanttekeningen bij. Verder letten we in deze cursus voor de duidelijkheid in het rekenwerk NIET op significante cijfers.
In dit deel I van de cursus bespreken we de basisbegrippen. Wat is temperatuur, wat is warmte, wat is warmtecapaciteit? We moeten op molecuulniveau kijken om dat te begrijpen. We kijken naar berekeningen als:
"We willen een halve liter water van 20°C opwarmen tot het kookpunt. Hoeveel warmte is er nodig?"
Hoeveel warmte komt er vrij als 2 kg water van 0°C verandert in 2 kg ijs van 0°C?
Hoeveel warmte komt er vrij als 2 kg water van 0°C verandert in 2 kg ijs van 0°C?
Misschien kun je wel overweg met dit soort sommetjes. We raden je ook dan tóch aan om dit deel 1 door te nemen. Want een paar kleine misverstandjes, of "slechte (reken)gewoontes" zijn meestal de reden dat je vastloopt in de wat ingewikkelder berekeningen.
Ook is het onmisbaar dat je formules kunt ómschrijven, bijvoorbeeld van v=s/t naar s=vxt.
Neem zonodig eerst de [microcursus] formules herschrijven / vergelijkingen oplossen door.
In deel 2: rekenbladmethodegaan we op basis van die kennis dan verder met:
"In een vat met een warmtecapaciteit van 75 J/K zitten 500 g water en 100 g ijs van 0,0 °C.
Bereken de massa stoom van 115°C die men aan het mengsel moet toevoegen om water van 40 °C te krijgen."
Dit zijn eigenlijk meerdere sommetjes uit deel 1, samengevouwen tot één probleem. We gaan uitleggen hoe je van elk van deze sommetjes een fluitje van een cent maakt ook als er ijs, stoom, calorimeters of wat ook bij te pas komt: met de tabelmethode.Bereken de massa stoom van 115°C die men aan het mengsel moet toevoegen om water van 40 °C te krijgen."
Er zijn eigenlijk maar vijf zeer eenvoudige formules nodig (waarvan er drie sterk op elkaar lijken), die iedereen kan onthouden, en verder wat gegevens uit een tabellenboek en...... systematisch werken.
| De waarden voor soortelijke warmte enz. die we in deze cursus gebruiken komen voornamelijk uit : Onderaan de cursus vind je nog oefenopgaafjes, met het antwoord gegeven, maar met de uitwerking verborgen. Die uitwerking kun je zichtbaar maken door op de bijbehorende link "Verborgen inhoud" te klikken. |  Binas Havo VWO |
Misschien is deze stof niet nieuw voor je, en mogelijk leerde je de formules:
\(Q_{in} = Q_{uit}\)
\(Q_{in} = m \cdot c \cdot(T_{eind}- T_{begin})\)
en \(Q_{uit} = m \cdot c \cdot(T_{begin}- T_{eind})\)
VERGEET ZE !!! . Je krijgt van ons een paar andere. Die lijken er veel op, maar scheppen minder verwarring.
Dan is er nog DE grote begripsverwarring: warmte geeft aan hoe warm iets is. Nee !!
3: Inwendige energie: beweging van moleculen
Neem een speeltuinschommel, en geef er een klein duwtje tegen: daardoor geef je de schommel een beetje energie, de schommel gaat een beetje heen en weer bewegen. Blijf duwtjes geven, of geef een grotere duw, en de schommel gaat steeds harder heen en weer bewegen.
Met moleculen werkt dat ook ongeveer zo, en die kunnen bovendien op allerlei manieren bewegen:
 ...... (afb. 1) ...... London South Bank University
...... (afb. 1) ...... London South Bank University(bewegingsmogelijkheden van een watermolecuul... artistieke impressie)
Bij het absolute nulpunt, 0 kelvin (-273,15 °C), staat alles stil. Gaan we dan energie toevoeren aan die stof, dan gaan de moleculen beetje bij beetje steeds heftiger bewegen. Andersom, haal energie uit de stof, en de moleculen gaan rustiger bewegen. Een blokje stof als geheel gaat hierdoor niet bewegen. Deze bewegingsenergie noemen we dan ook "inwendige energie".
Verder is er ook energie nodig als je de krachten tussen moleculen wil verkleinen, zodat ze ten opzichte van elkaar kunnen gaan bewegen (vaste stof wordt vloeistof). Ook dat zit in die "inwendige energie".
4: Wat is "temperatuur"?
 | 4.1 Temperatuur Dankzij die bewegingsenergie kun je "temperatuur" meten: door luchtmoleculen tegen een thermometer te laten botsen gaan de alcoholmoleculen in de thermometer harder trillen. Merk op dat ze daardoor ook meer ruimte zullen innemen (honderd doodstil staande mensen kun je dichter op elkaar proppen dan 100 dansende mensen). Ook de alcoholmoleculen hebben dan meer ruimte nodig, de alcohol zet uit. Dat kun je aflezen. |
Temperatuur is een maat voor de gemiddelde bewegingsenergie van de moleculen in een stof.
[tr][td] Let op: omdat moleculen elkaar constant duwtjes geven is het onzin te spreken van de "temperatuur van een molecuul".
In de afbeelding kun je een animatie zien van moleculen in een gas. Een paar moleculen zijn rood gekleurd om beter te kunnen volgen. Door onderlinge botsingen verandert hun snelheid, en dus hun bewegingsenergie, voortdurend. De totale bewegingsenergie, en daardoor de gemiddelde bewegingsenergie per molecuul, verandert daarbij echter niet: [/td][td]
 ......(afb. 2)Wikipedia
......(afb. 2)Wikipedia[/td][/tr]
[tr][td]

(afb. 3)bron: Planet-Terre
[/td][td]De grootheid temperatuur geven we aan met het symbool T, en de bijbehorende SI-eenheid is kelvin (K).
Bij 0 K is de gemiddelde bewegingsenergie van de moleculen 0 J. Alle moleculen staan dus stil.
Stiller dan stil kan niet. Daarom is 0 K het absolute nulpunt.
De kelvin en de graad Celsius zijn even grote eenheden, alleen het nulpunt ligt anders (zie afbeelding hiernaast).
Kelvin kun je daarom makkelijk omreken in graden Celsius met :
\( T_{(K)} = 273,15 + T_{(°C)}\)
Het is een goede en vaak onmisbare gewoonte om met SI-eenheden, en hier dus o.a. met kelvin, te rekenen. Toch zul je ons hier vaak met °C zien rekenen. Voor uitleg waarom dat hier wel kan en mag zie de volgende paragraaf. [/td][/tr]
4.2 Verandering van temperatuur, ΔT
In calorimeterberekeningen hebben we zelden te maken met één temperatuur.
Het zal vrijwel altijd gaan om een begintemperatuur Tbegin, en dan gebeurt er iets met de energie, en krijg je een eindtemperatuur Teind.
We hebben te maken met een verandering van temperatuur.
"Verandering van temperatuur" noteren we als
\(\Delta T\)
. [/color][/b]Even iets zéér belangrijks over die
\( \Delta T\)
:In de natuurkunde is het de vaste afspraak om "verandering van" (iets) áltijd te berekenen met :
\( \Delta (iets) = (iets)_{eind} - (iets)_{begin} \)
Of het nu gaat over snelheid, plaats, temperatuur, volume, noem maar op. Correcte uitkomsten van berekeningen zijn altijd op deze afspraak gebaseerd.
Onze eerste formule is dan ook:
[tr][td]
\( \Delta T = T_{eind} - T_{begin} \)
[/td][/tr]Dat kan en mag in dit geval omdat we Tbegin en Teind alleen maar in verschilberekeningen gebruiken.
Bij zo'n berekening geeft 298 K - 277 K (= 21 K) immers precies hetzelfde resultaat als 25°C -4°C (= 21°C).
We zouden voor de netheid beter altijd de kelvin gebruiken. Dat heeft echter twee nadelen: de kans op omrekenfouten wordt groter, en temperaturen in kelvin zijn voor de meesten weinigzeggende getallen.
Voor ΔT, en in de eenheden voor warmtecapaciteit e.d. gebruiken we in deze cursus wél de kelvin.
Rekenvoorbeelden:
[tr][td]Een wegdek warmt op van -20°C naar +35°C. Wat is de verandering van temperatuur?
Tbegin = -20°C
Teind = +35°C
ΔT = ?? K
ΔT = Teind - T begin = 35 - (-20) = + 55 K[/td][td]Een radiator met een temperatuur van +85°C krijgt een verandering van temperatuur van -33 K. Wat wordt de eindtemperatuur?
Tbegin = +85°C
ΔT = -33 K
Teind = ?? °C
ΔT = Teind - T begin ==> Teind = ΔT + T begin = -33 + 85 = + 52°C [/td][/tr]
Ja, ΔT kan positief óf negatief zijn! Dit moeten we consequent volhouden. In formules waarmee we verderop gaan rekenen hebben die plussen of minnen grote invloed!!
We kunnen hetzelfde sommetje ook netjes in kelvin uitwerken.
Voor het eindresultaat heeft dat geen gevolgen, kijk maar in deze
Verborgen inhoud
.5: Wat is "warmte"?
Als je energie toevoert aan een deel van een voorwerp, dan gaat een deel van de moleculen in dat voorwerp heftiger bewegen. Die geven daardoor ook duwtjes tegen hun buurmoleculen, die daardoor ook heftiger gaan bewegen. Dat heet dan geleiding. De energie verplaatst zich zo van een plaats met hoge temperatuur naar een plaats met lage temperatuur.
 ...... (afb. 4)......GCSE.com
...... (afb. 4)......GCSE.com...... Geleiding van warmte in een vaste stof,
moleculen geven bewegingsenergie aan elkaar door)
Dat geldt ook voor bijvoorbeeld een warm blokje metaal in koud water: even wachten en er ontstaat thermische evenwicht, blokje en water krijgen een gelijke temperatuur.
Daarmee komen we nu aan wat warmte WÉL is:
Warmte is de energie die als gevolg van temperatuursverschillen van een voorwerp met hogere temperatuur naar een voorwerp met lagere temperatuur stroomt.
De grootheid warmte geven we aan met het symbool Q, en de bijbehorende eenheid is joule (J), de eenheid van energie.Behalve opwarmen kun je een voorwerp ook laten afkoelen: de moleculen van het voorwerp dragen dan hun energie over aan moleculen buiten het voorwerp, bijvoorbeeld een lepel hete soep warmt de lucht er rondom op, en wordt daardoor zelf kouder.
Oh, en nu we het er toch over hebben, "kou" bestaat niet in de natuurkunde. Als je je handen op een blok ijs legt stroomt er geen kou uit het ijs je handen in. Warmte stroomt uit je handen.
6: Warmtecapaciteit
Als je een hoeveelheid energie toevoert aan een voorwerp, zal de temperatuur van dat voorwerp veranderen. Als je twee keer zoveel energie toevoert, dan zal de temperatuur twee keer zo sterk veranderen.
Het ene voorwerp zal in temperatuur meestal meer of minder veranderen dan het andere voor eenzelfde hoeveelheid warmte. We kunnen dus spreken van de "warmtecapaciteit" van een voorwerp:
Warmtecapaciteit ( C ) is een maat voor de hoeveelheid warmte (energie) die nodig is om een voorwerp 1 kelvin in temperatuur te laten stijgen
in formule:
\( C = \frac{Q}{\Delta T} \)
Warmte (energie) druk je uit in joule, verandering van temperatuur in kelvin, warmtecapaciteit dus in joule per kelvin (J/K)
In warmteberekeningen gebruik je deze formule meestal in een iets andere vorm geschreven.
Dat geeft ons onze tweede formule:
[tr][td]
\( Q = C \cdot \Delta T\)
[/td][/tr]Rekenvoorbeelden:
[tr][td]Om een blok marmer van 20°C in temperatuur te verhogen naar 35°C is 26 400 J warmte nodig. Wat is de warmtecapaciteit van het blok?
Tbegin = +20°C
Teind = +35°C
Q = 26 400 J
Cblok = ?? J/K
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 35 - 20 = +15 K
Q = C·ΔT dus Cblok= Q/ΔT = 26 400/15 = 1760 J/K
[/td][td]Een loden kogel met een warmtecapaciteit van 25 J/K koelt af van 300 naar 20°C. Hoeveel warmte wordt afgestaan aan de omgeving?
Tbegin = +300°C
Teind = +20°C
Ckogel = 25 J/K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 20 - 300 = -280 K
Q = C·ΔT = 25 x -280 = -7000 J [/td][/tr]
Ja, Q (de warmte) in het rechtse voorbeeld is negatief (omdat ΔT negatief was)! Blijkbaar betekent dat dat de warmte het voorwerp UITstroomt. Misschien even wennen.
plus: het voorwerp ontvangt energie. (of snelheid, of massa, of wat ook)
min: het voorwerp staat energie af. (of snelheid, of massa of wat ook)
min: het voorwerp staat energie af. (of snelheid, of massa of wat ook)
Reken consequent met die plusjes en minnetjes, en je berekeningen komen altijd uit.
7: Soortelijke warmtecapaciteit (soortelijke warmte)
In het vorige hoofdstuk hadden we het nog over een voorwerp, (een BLOK marmer, een loden KOGEL) en hoeveel warmte (energie) daar in moest om de temperatuur met 1 K te verhogen (de warmtecapaciteit). Het is natuurlijk logisch dat als dat voorwerp twee keer zo zwaar wordt, dat er dan ook twee keer zoveel warmte in of uit moet om dezelfde verandering van temperatuur te krijgen.
De warmtecapaciteit van een voorwerp hangt dus af van de massa.
Iets minder voor de hand liggend is dat de warmtecapaciteit van een voorwerp óók afhangt van de soort stof waarvan het gemaakt is. De moleculen in een stof oefenen behoorlijke krachten op elkaar uit om bij elkaar te blijven, en de atomen in die moleculen ook. Naarmate die krachten groter zijn kost het meer energie om er beweging in te krijgen.
De warmtecapaciteit van een voorwerp hangt dus af van de stof waarvan het gemaakt is.
Een paar voorbeelden uit BINAS:
1 kg water heeft een warmtecapaciteit van 4180 J/K;
1 kg marmer heeft een warmtecapaciteit van 880 J/K;
1 kg lood heeft een warmtecapaciteit van 128 J/K;
Je ziet, dat scheelt nogal wat van stof tot stof.
In hoofdstuk 6 berekenden we de warmtecapaciteit van het blok marmer op 1760 J/K, het kostte 1760 joule om het blok 1 K in temperatuur te verhogen. Met de wetenschap dat het 880 joule kost om 1 kg marmer 1 K in temperatuur te doen stijgen, berekenen we al snel dat de massa van dat blok marmer 1760/880 = 2 kg geweest moet zijn.
De warmtecapaciteit van 1 kg van een stof noemen we de soortelijke warmtecapaciteit "c"
(vaak kortweg "soortelijke warmte").
Soortelijke warmte(capaciteit) "c" druk je dus uit in joule per kilogram en per kelvin
(vaak kortweg "soortelijke warmte").
Soortelijke warmte(capaciteit) "c" druk je dus uit in joule per kilogram en per kelvin
\(\frac{J}{kg \cdot K}\)
[/color][/b]in formule:
\( c = \frac{Q}{m \cdot \Delta T} \)
Iets anders geschreven leidt dat tot onze derde formule (die héél erg op de tweede lijkt):
[tr][td]
De warmtecapaciteit "C" van ons voorwerp is nu opgesplitst in de massa "m" van het voorwerp en de soortelijke warmtecapaciteit "c" van de stof waarvan het voorwerp is gemaakt.\( Q = m \cdot c \cdot \Delta T\)
[/td][/tr]Rekenvoorbeelden:
[tr][td]"We willen een halve liter water van 20°C opwarmen tot het kookpunt. Hoeveel warmte is er nodig?"
Tbegin = +20°C
Teind = +100°C
mwater= 0,5 kg (een halve liter water heeft een massa van 500 g)
cwater = 4180 J/kg·K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 100 - 20 = +80 K
Q = m·c·ΔT = 0,5 x 4180 x 80 = 167 200 J
[/td][td]Bij het afkoelen van een loden kogel van 300 naar 20°C wordt 7000 J warmte afgestaan aan de omgeving. Wat is de massa van de kogel?
Tbegin = +300°C
Teind = +20°C
clood = 128 J/kg·K
Q = -7000 J (minnetje! , want het voorwerp raakt warmte kwijt)
mlood = ?? kg
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 20 - 300 = -280 K
Q = m·c·ΔT dus m = Q/(c·ΔT) = -7000 : (128 x -280) = 0,195 kg [/td][/tr]
Niet onbelangrijk om te beseffen: een stof heeft in de verschillende fasen verschillende eigenschappen. Dat geldt zeker ook voor de stofeigenschap "soortelijke warmte". Bijvoorbeeld:
ijs, c= 2 200 J/kg·K
water, c= 4 180 J/kg·K
waterdamp: c = 2027 J/kg·K (bij gemiddelde atmosferische druk)
water, c= 4 180 J/kg·K
waterdamp: c = 2027 J/kg·K (bij gemiddelde atmosferische druk)
In berekeningen waarbij fasen veranderen kun je de verschillende fasen van één stof dus net zo goed als verschillende stoffen beschouwen.
8: Fase-overgangen: latente warmte
Moleculen in vaste stoffen oefenen forse krachten op elkaar uit. Ook in vloeistoffen zijn die krachten nog aanzienlijk. Een blokje ijzer, maar ook een waterdruppel, vallen niet zomaar uit elkaar. Er is heel wat energie nodig om de moleculen uit een vaste stof losser te maken tot een vloeistof, of uit een vloeistof geheel los te maken tot losse gasmoleculen.
 ......
......  (afb. 5)......Purdue University Dept. of Chemistry
(afb. 5)......Purdue University Dept. of Chemistry(moleculen in een vloeistof resp. een gas... artistieke impressie)
Dat dat veel energie kost merk je goed als je een beetje zweet: voor het verdampen van dat beetje zweet wordt veel warmte aan je lichaam onttrokken. Ook zo als je water kookt: je blijft energie (warmte) toevoeren aan je pan op het fornuis, maar het water wordt niet warmer dan 100°C terwijl het vloeibare water in waterdamp van 100°C verandert.
[tr][td]Je kent vast wel zo'n grafiekje:-->
hier hebben we de warmte nodig om 1 kg ijs van -100°C te veranderen in 1 kg stoom van +200°C in ongeveer de juiste verhoudingen weergegeven. Merk op dat het verdampen ongeveer 2/3 van de totale energie vraagt!!
Om 1 kg water van 100°C te veranderen in waterdamp van 100°C is maar liefst 2 260 000 J aan warmte nodig!! (en voor 2 kg is dat dus ook 2 x zoveel).
Onderschat ook het smelten van ijs van 0°C tot water van 0°C niet: 334 000 J voor 1 kg !!
[/td][td]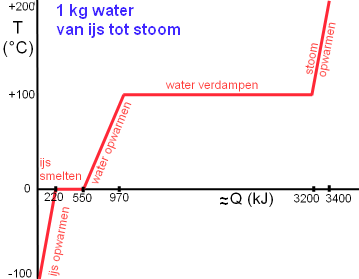
...........(afb. 6)...... warmte en fase-overgangen, © JvdV
[/td][/tr]
hier hebben we de warmte nodig om 1 kg ijs van -100°C te veranderen in 1 kg stoom van +200°C in ongeveer de juiste verhoudingen weergegeven. Merk op dat het verdampen ongeveer 2/3 van de totale energie vraagt!!
Om 1 kg water van 100°C te veranderen in waterdamp van 100°C is maar liefst 2 260 000 J aan warmte nodig!! (en voor 2 kg is dat dus ook 2 x zoveel).
Onderschat ook het smelten van ijs van 0°C tot water van 0°C niet: 334 000 J voor 1 kg !!
[/td][td]

...........(afb. 6)...... warmte en fase-overgangen, © JvdV
[/td][/tr]
De warmte nodig om een stof van fase te laten veranderen noemen we "latente warmte" ("L")
(latent = onmerkbaar aanwezig, de temperatuur verandert niet terwijl er toch warmte wordt toe- of afgevoerd.)
Latente warmte is per stof verschillend.(latent = onmerkbaar aanwezig, de temperatuur verandert niet terwijl er toch warmte wordt toe- of afgevoerd.)
De warmte nodig om 1 kg van een vaste stof te smelten noemen we de soortelijke smeltwarmte ("Ls")
De warmte nodig om 1 kg van een vloeistof te verdampen noemen we de soortelijke verdampingswarmte ("Lv")
De temperatuur verandert hier niet bij, dus latente warmte drukken we uit in
Voor latente warmte is er geen internationaal afgesproken afkorting. In deze cursus gebruiken we de "L" van latent met de "s" van smelting of de "v" van verdamping ).
De warmte nodig om 1 kg van een vloeistof te verdampen noemen we de soortelijke verdampingswarmte ("Lv")
De temperatuur verandert hier niet bij, dus latente warmte drukken we uit in
\(\frac{J}{kg}\)
[/color][/b] Voor latente warmte is er geen internationaal afgesproken afkorting. In deze cursus gebruiken we de "L" van latent met de "s" van smelting of de "v" van verdamping ).
in formule:
\( L = \frac{Q}{m} \)
In warmteberekeningen gebruik je deze formule meestal in een iets andere vorm geschreven.
Dat geeft ons onze vierde formule (die heel erg op de tweede en derde lijkt) :
[tr][td]
\( Q = m \cdot L \)
[/td][/tr]Rekenvoorbeelden:
[tr][td]In een koelbox met 3 kg ijsblokjes van 0°C "lekt" per uur 83 500 J aan warmte uit de omgeving binnen. Hoe lang duurt het voordat alle ijs gesmolten is?
m= 3 kg
Ls = 334 000 J/kg
Q = ?? J
Q= m·Ls = 3 x 334 000 = 1 002 000 J
t= 1 002 000 (J) / 83500 (J/h) = 12 h
[/td][td]Een loden kogel met een massa van 0,195 kg vraagt
4 875 J om te smelten. Wat is de smeltwarmte van lood?
Q= 4 875 J
m = 0,195 kg
Ls = ?? J/kg
Ls= Q/m = 4 875 / 0,195 = 25 000 J/kg
(en dat is een reële tabelwaarde) [/td][/tr]
Net als bij afkoelen en opwarmen geldt: er is evenveel energie nodig om 1 kg water te verdampen tot 1 kg damp, als dat er energie vrijkomt bij het condenseren van 1 kg damp tot 1 kg water. De condensatiewarmte (energie die vrijkomt als de damp weer terug condenseert) is dus even groot als de verdampingswarmte. Datzelfde geldt voor smelten en stollen, en natuurlijk ook voor sublimeren en rijpen.
Voor het verdampen van 1 kg water is 2 260 000 J energie nodig. Daarmee zou je 540 kg water 1 K kunnen opwarmen! Dit verschijnsel kun je nuttig gebruiken, want die energie krijg je weer terug als de damp weer condenseert. Mede daarom is stoom zo'n geliefd middel om energie te transporteren: per kg kun je er veel meer energie instoppen en weer terug uithalen dan uit heet water.
9: Wet van behoud van energie: som van de warmtestromen is nul
We voegen 1 kg water van 20°C samen met 1 kg water van 80°C. Wat wordt de eindtemperatuur?
..............................
 (afb. 7)
(afb. 7)Je hoeft geen genie te zijn om te snappen dat er in elk geval 2 kg water in die grote maatbeker terechtkomt. En een beetje snuggere basisschoolleerling zal al gauw vermoeden dat de eindtemperatuur in die grote beker 50°C zal zijn, het gemiddelde van die 20°C en die 80°C.
En zo blijkt zelfs een basisschoolleerling twee heel belangrijke natuurkundige gegevens eigenlijk al te kennen zonder die ooit geleerd te hebben:
1) Als er tussen twee stoffen een temperatuurverschil bestaat, ontstaat er een warmtestroom totdat beide stoffen een gelijke temperatuur hebben.
2) De energie die de ene stof daarbij afstaat is gelijk aan de energie die de andere stof opneemt.
Zoiets kun je op intuïtie nog wel oplossen. Tóch moeten we dit eens even netjes doen, want met intuïtie krijgen we het niet meer opgelost als we wat ingewikkelder gegevens krijgen (de opgaven zélf worden eigenlijk nooit ingewikkelder). Nu kunnen we alvast even oefenen.
We gaan er even van uit dat er geen warmte van binnen naar buiten gaat of andersom: dus, wat de ene stof aan warmte afstaat wordt door de andere stof opgenomen, de optelsom van die warmtestromen is gewoon 0.
Dit wordt dan gelijk de 5e en laatste formule die we nodig hebben:
[tr][td]
\(Q_1 + Q_2 + Q_3 + {.......} = 0\)
[/td][/tr]Laten we eens zien of die 50°C klopt:
[tr][td] 1 kg water met een temperatuur van 20°C wordt opgewarmd tot 50°C. Hoeveel warmte is hiervoor nodig?
Tbegin = +20°C
Teind = +50°C
mwater= 1 kg
cwater = 4180 J/kg·K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 50 - 20 = +30 K
Q = m·c·ΔT = 1 x 4180 x 30 = 125 400 J
[/td][td]1 kg water met een temperatuur van 80°C wordt afgekoeld tot 50°C. Hoeveel warmte komt hierbij beschikbaar?
Tbegin = +80°C
Teind = +50°C
mwater= 1 kg
cwater = 4180 J/kg·K
Q = ?? J
eerste stap:
ΔT = ?? K
ΔT = Teind - T begin = 20 - 50 = -30 K
Q = m·c·ΔT = 1 x 4180 x -30 = -125 400 J
[/td][/tr][tr][td] check:
Qkoud water + Qwarm water = 125 400 + (-125 400) = 0[/td][/tr]
Samenvatting: Grootheden, eenheden, definities, formules
grootheid: MASSA ( m )
definitie: de hoeveelheid van een stof
SI-eenheid: kilogram (kg)
grootheid: TEMPERATUUR ( T )
definitie: een maat voor de bewegingsenergie van deeltjes in een hoeveelheid stof
SI-eenheid: kelvin (K) (we zullen hier overigens vaak met graden Celcius (°C) werken)
De eenheid K is overigens even groot als de eenheid °C. Alleen het nulpunt ligt anders:
0 K is dus - 273°C (eigenlijk -273,15°C, maar dat is niet zo belangrijk)
Nou zullen we in deze cursus vaak rekenen met verandering van temperatuur (ΔT) , (spreek uit: delta T). Omdat 1 K even groot is als 1°C maakt het dan weinig meer uit of we kelvin of graden Celsius gebruiken. Een ΔT van 21 K is een precies even grote verandering als een ΔT van 21°C.
temperatuurverandering is eindtemperatuur minus begintemperatuur
\(\Delta T = T_{eind} - T_{begin}\)
grootheid: WARMTE ( Q )
definitie: Warmte is de energie die als gevolg van een temperatuurverschil door een warmtegeleidende wand stroomt. Warmte is een moeilijk begrip. (VERWAR HET NIET MET TEMPERATUUR!!) Warmte is een energiestroom. Je kunt dus niet spreken over 'de warmte' van een hoeveelheid stof. Geen paniek, je zult zien dat dit in de praktijk veel simpeler is dan het lijkt.
SI-eenheid: joule (J) (niet toevallig dezelfde als van energie)
grootheid: (voorwerps)WARMTECAPACITEIT ( C )
definitie: de hoeveelheid energie in joule die nodig is om een voorwerp één kelvin in temperatuur te laten stijgen. Deze is natuurlijk alleen voor precies dezelfde voorwerpen gelijk. Een groter voorwerp zal een grotere warmtecapaciteit hebben.
SI-eenheid: joule per kelvin (J/K) (de massa (kg) staat niet in deze formule: hij is vastgesteld voor het voorwerp, de massa is daar al in verrekend)
Warmte is de (voorwerps-) warmtecapaciteit maal de temperatuurverandering
\(Q= C \cdot \Delta T\)
grootheid: SOORTELIJKE WARMTECAPACITEIT ( c )
definitie: de hoeveelheid energie in joule die nodig is om één kilogram van een stof één kelvin in temperatuur te laten stijgen. Deze is voor alle stoffen verschillend. Je kunt het voor de meeste stoffen in een tabellenboek vinden.
SI-eenheid: joule per kilogram per kelvin (J/kg·K) :
Warmte is de massa maal de (soortelijke) warmtecapaciteit maal de temperatuurverandering
\(Q=m \cdot c \cdot \Delta T\)
FASE: de toestand waarin een stof zich bevindt.
In deze cursus beperken we ons tot de drie belangrijkste fasen: vaste stof, vloeistof, gas (damp)
grootheid: LATENTE WARMTE ( L... ) (smelt-, stollings-, verdampings- en condensatiewarmte.)
definitie: de hoeveelheid energie in joule die nodig is (of die vrijkomt) bij het veranderen van de fase van een kilogram van een stof (bij gelijkblijvende temperatuur)dus bijvoorbeeld de warmte die nodig is om een kg ijs te laten smelten bij 0°C, of juist de warmte die vrijkomt als een kg water een kg ijs wordt.
SI-eenheid: joule per kilogram (J/kg) (de temperatuur (K) staat niet in deze formule: die verandert niet bij een fase-overgang: verdampen - condenseren - smelten - stollen)
Warmte is de massa maal de (soortelijke) fase-overgangswarmtecapaciteit
\(Q=m \cdot L_{...}\)
1) Als er tussen twee stoffen een temperatuurverschil bestaat, ontstaat er een warmtestroom totdat beide stoffen een gelijke temperatuur hebben.
2) De energie die de ene stof daarbij afstaat is gelijk aan de energie die de andere stof opneemt.
De som van alle warmtestromen is nul.
\(Q_1 + Q_2 + Q_3 + {.......} = 0\)
plus: de stof ontvangt energie. (of snelheid, of massa, of wat ook)
min: de stof staat energie af. (of snelheid, of massa of wat ook)