1 van 2
functie
Geplaatst: do 30 jul 2020, 18:27
door ukster
Wat is de analytische oplossing van de rotatiehoek θ van de functie f(x)=sin(x)/x, waarbij de grafiek nog als functie kan worden aangemerkt.
Volgens mij is dat het geval als er slechts 1 verticale raaklijn is.
Re: functie
Geplaatst: do 30 jul 2020, 19:20
door flappelap
Ik persoonlijk heb geen idee wat je met je vraag bedoelt.
Re: functie
Geplaatst: do 30 jul 2020, 19:59
door ukster

- vertical line test 2917 keer bekeken
Door rotatie van een functie f(x) om de oorsprong kan de situatie optreden dat er voor een waarde van x meerdere functiewaarden bestaan. Dit levert dus wel een grafiek op maar is
geen functie! (vertical line test bovenste plaatje)
Ik vermoed dat de grens van
wel een functie/geen functie ligt bij precies 1 verticale raaklijn.
De rotatieformule voor een functie f(x) in een x-y assenstelsel is:

- rotatieformule 2917 keer bekeken
θ is de rotatiehoek
Re: functie
Geplaatst: vr 31 jul 2020, 10:22
door tempelier
Lijkt me niet als ik je goed begrijp.
Zie: \(y=x^2\)
Re: functie
Geplaatst: vr 31 jul 2020, 18:30
door ukster
y=x
2 is een functie (vertical line test)
y=x
2 is een
niet 1 op 1 functie (horizontal line test)
Er is wel een inverse van y=x
2 , maar dit is dus
geen functie!

- inverse 2727 keer bekeken
Re: functie
Geplaatst: vr 31 jul 2020, 18:37
door tempelier
Je komt nu met een nieuwe eis volgen mij.
PS.
y=x2 heeft geen inverse.
PS.
Men kan de functie natuurlijk wel reduceren dan is er wel een inverse.
Re: functie
Geplaatst: vr 31 jul 2020, 18:56
door ukster
Het gaat erom of de grafiek van de functie
sin(x)/x na een bepaalde rotatie om de oorsprong nog wel een functie is.(do the vertical line test)
rotatieformule:
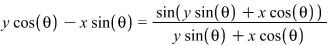
- rotatieformule 2720 keer bekeken
op basis van een Mapleplot schat in dat een rotatie > 67° geen functie meer oplevert (bij precies 1 verticale raaklijn)
De vraag blijft staan hoe deze kritische rotatiehoek analytisch kan worden bepaald!
Re: functie
Geplaatst: vr 31 jul 2020, 19:18
door tempelier
Lastig.
Ik zou het zoeken in een rechte snijlijn.
Elke snijlijn bepaald een maximale draai hoek.
Re: functie
Geplaatst: vr 31 jul 2020, 20:54
door RedCat
Alternatief:
Zoek de raaklijn aan f(x) = sin(x)/x met de maximale richtingscoëfficient.
Noem de richtingshoek van die raaklijn alpha.
Dan is je maximale rotatiehoek theta =
\(\theta = \frac{\pi}{2} - \alpha\)
Na rotatie over deze hoek theta staat die raaklijn precies verticaal (= parallel aan de y-as).
Ik kom zo uit op theta = 1.159492829676... rad = 66.434045516136...°
Re: functie
Geplaatst: vr 31 jul 2020, 23:43
door ukster
Slim gevonden zeg..

Het inflection point van sin(x)/x ligt op x=-2,08 (voor het interval -4..0)
De afgeleide cos(x)/x-sin(x)/x
2 heeft op dat punt de maximale richtingscoefficient tan(α)=0,43618, dus α=0,4113 rad. θ
max=π/2-α=1,159 rad= 66,43°
Re: functie
Geplaatst: za 01 aug 2020, 00:51
door CoenCo
ukster schreef: ↑do 30 jul 2020, 19:59
vertical line test.png
Door rotatie van een functie f(x) om de oorsprong kan de situatie optreden dat er voor een waarde van x meerdere functiewaarden bestaan. Dit levert dus wel een grafiek op maar is
geen functie! (vertical line test bovenste plaatje)
Ik vermoed dat de grens van
wel een functie/geen functie ligt bij precies 1 verticale raaklijn.
De rotatieformule voor een functie f(x) in een x-y assenstelsel is: rotatieformule.png
θ is de rotatiehoek
Vermoed je dit voor álle functies, of specifiek deze (sin(x))/x functie? Tegenvoorbeeld: Als je alleen sin(x) neemt, en deze 45graden roteert, dan heb je oneindig veel verticale afgeleiden, maar nog steeds een functie lijkt me.
Re: functie
Geplaatst: za 01 aug 2020, 13:31
door ukster
Voor alle functies.
Voor elke waarde van de onafhankelijke variabele van de 45° geroteerde sin(x) functie hoort nog steeds 1 functiewaarde.
voor θ>45° kun je volgens de definitie van de vertical line test niet meer van een functie spreken.
Re: functie
Geplaatst: za 01 aug 2020, 13:55
door ukster
Ik zie echter niet hoe de laatste uitdrukking hieronder de 3 verschillende y- waarden bevat voor x=0

- 3 verschillende y waarden 2546 keer bekeken
Re: functie
Geplaatst: za 01 aug 2020, 14:22
door ukster
Mathematica gaat iets verder.

- complex oplossing 2533 keer bekeken
Re: functie
Geplaatst: za 01 aug 2020, 15:32
door tempelier
Vond Maple ze niet via evalf dat zou eigenlijk wel moeten.