1 van 1
Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: za 03 mar 2007, 20:00
door hond
Ik wil de massa van een planeet bereken dmv de 3e wet van Kepler. Ik heb de formule omgevormd, maar als ik bijvoorbeeld de gevens van de aarde tov de zon invul, kom ik massa's uit die helemaal niet kloppen.
Ik heb
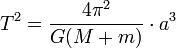
omgevormd tot

Ik snap mijn fout niet [rr]
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: za 03 mar 2007, 21:27
door Jan van de Velde
mijn formuleverbouwing op het kladpapiertje hier voor mijn neus lijkt als twee druppels water op de jouwe. Vul je ergens verkeerde gegevens in of zo?
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: za 03 mar 2007, 22:01
door hond
Stel, we willen de massa van de aarde te weten komen
a (halflange as)= 149,597,887,500 m
T (periode)= 30780549,54 s
G = 6.67 × 10−11 Nm²/kg²
m (massa zon)= 1.988 435×10^30 kg
M= (4π².(149,597,887,500 m)³-(30780549,54 s)²(6.67 × 10−11 Nm²/kg²)(1.988 435×10^30 kg))/(30780549,54 s)²(6.67 × 10−11 Nm²/kg²)
= 1,030634487 x 10^29 kg
terwijl dat 5.9742×10^24 kg moet zijn.
Vreemd

Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: za 03 mar 2007, 22:40
door Jan van de Velde
één dingetje heb ik al, maar dat is een betrekkelijk detail: de omlooptijd van de aarde is 31558149 s.
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: ma 05 mar 2007, 20:20
door aaargh
Ik denk dat de massa van de zon zo abundant groot is vergeleken met de massa van de Aarde dat die kleine m gewoon verdwijnt en als je een waarde invult die er slechts een klein beetje vanaf zit, kom je al compleet verkeerde waarden uit.
Als ik de waarde's invul en als massa van de aarde 0 neemt, dan komt het ook quasi uit.
Die formule is overigens niet de wet van Kepler, Kepler zei enkel dat het kwadraat van de omloooptijd evenredig was met de halflange as tot de derde. Hij wist nog niet welke constantne hij daar moest inpassen.
PS: als ik het even met het rekenmachin plot zie ik dat een verchil van enkele tientallen seconden omlooptijd de massa van de aaarde enorm laat versprngen.
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: ma 05 mar 2007, 20:22
door Jan van de Velde
PS: als ik het even met het rekenmachin plot zie ik dat een verchil van enkele tientallen seconden omlooptijd de massa van de aaarde enorm laat versprngen.
als dat waar is:
één dingetje heb ik al, maar dat is een betrekkelijk detail: de omlooptijd van de aarde is 31558149 s.
dan is dit dus niet zo'n "betrekkelijk detail".
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: za 19 mei 2007, 22:45
door sluys
De wet van Kepler zegt dat de omlooptijd van een planeet om de Zon gegeven wordt door de afstand tot de Zon. De massa van de planeet is dus niet belangrijk. Als de omlooptijd van de Aarde om de Zon niet afhangt van haar massa, dan kun je de massa van de Aarde dus ook niet bepalen uit de omlooptijd.
De reden is inderdaad dat de massa van de Aarde veel kleiner is dan die van de Zon. In jouw formule is M de massa van de Aarde, m die van de Zon. Dan geldt dus: m = 1.9891x10^30 kg (nauwkeuriger is de zonsmassa niet bekend), m+M = 1.9891x10^30 + 5.9742x10^24 = 1.9891x10^30 kg. Dus m+M ~ M. De massa van de Aarde doet er dus niet toe.
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: za 19 mei 2007, 22:56
door eendavid
Wat je wel eens kan doen, is de masa van de aarde bepalen uit de omlooptijd van de maan. Het zijn de omlooptijden van kunstsatellieten (met massa 0 laat ons zeggen) die tot behoorlijk nauwkeurige metingen van de massa van onze aarde hebben geleid, maar de maan zal voor deze berekening allicht wel zinvolle resultaten geven (onderstel de massa van de maan bijvoorbeeld gekend

).
Dat G zo slecht bepaald is natuurlijk oervervelend.
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: wo 08 aug 2007, 10:20
door thermo1945
Dat G zo slecht bepaald is natuurlijk oervervelend.
Er zijn waarnemingen die er op wijzen, dat
G niet volstrekt constant is.
Helaas weet ik de bron(-nen) niet meer.
Dat kan de reden zijn voor het gering aantal significante cijfers.
Wat je wel eens kan doen, is de masa van de aarde bepalen uit de omlooptijd van de maan.
Hiermee sla je de spijker op de kop
hond schreef:Ik wil de massa van een planeet bereken dmv de 3e wet van Kepler. ...
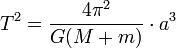
T en
a behoren bij het ronddraaiende object.
M is de massa van het centrale hemellichaam.
m wordt vaak verwaarloosd t.o.v.
M.
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: wo 08 aug 2007, 23:30
door gemertp
eendavid schreef:Wat je wel eens kan doen, is de masa van de aarde bepalen uit de omlooptijd van de maan. Het zijn de omlooptijden van kunstsatellieten (met massa 0 laat ons zeggen) die tot behoorlijk nauwkeurige metingen van de massa van onze aarde hebben geleid, maar de maan zal voor deze berekening allicht wel zinvolle resultaten geven (onderstel de massa van de maan bijvoorbeeld gekend

).
Dat G zo slecht bepaald is natuurlijk oervervelend.
Als je de maan gebruikt komt er wel een wat grotere onnauwkeurigheid in, omdat de maan nog een redelijke massa heeft vergeleken met de aarde (anders dan de aarde vergeleken met de zon).
Re: Massa van een planeet berekenen dmv 3e wet van Kepler
Geplaatst: do 09 aug 2007, 12:43
door eendavid
Ik denk niet dat je het probleem volledig hebt begrepen. Wat je kan berekenen is M+m=getal.
Stel we doen dit met de zon dan is M 333000 keer zo groot dan m. Dan moet je liefst getal en M tot op veel cijfers na de komma kennen. Maar aangezien dat getal omgekeerd evenredig is met G ken je dat niet: getal ken je op zijn best tot 3 cijfers na de komma, en je moet het minstens tot 5 cijfers na de komme kennen.
Stel we doen dit met de maan, dan is M ongeveer 1/100 van m. De nauwkeurigheid van getal wordt nu voldoende benut, want het is dezelfde als de nauwkeurigheid voor m.
@Thermo:
Wiki geeft daar een referentie van, maar het lijkt me zinvol dat voorlopig te wijten aan de moeilijkheid van het experiment eerder dan aan het varierend zijn van G.
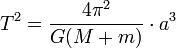 omgevormd tot
omgevormd tot 
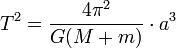 omgevormd tot
omgevormd tot 