[microcursus] goniometrie: sinus, cosinus, tangens (basis)
Geplaatst: do 03 jan 2008, 20:43
Er is ook een volledig overzicht van alle cursussen, FAQ's en handleidingen .
Bij deze cursus zijn ook een aantal oefenopgaven gemaakt, deze vind je onder de cursus.
Als je van deze cursus gebruik maakt, willen we je vriendelijk vragen te laten weten wat je er van vond:
---------------------------------------------------------------------------------------
[microcursus] Goniometrie: sinus, cosinus en tangens (basis)
Auteurs: StrangeQuark , TD , Jan van de Velde
Inhoudsopgave
Wat is goniometrie? Het woord goniometrie komt van het Oudgriekse woord γωνία (goonia) dat "hoek" betekent.
Sinus, cosinus en tangens zijn wiskundige gereedschappen om met hoeken te werken. Je komt ze overal in natuurkunde en techniek tegen. Bij het bouwen van bruggen en huizen, spiegels en lenzen, samenstellen en ontbinden van krachten, bij alle vormen van radiocommunicatie, bij radar, in je computer. Kortom, overal waar hoeken belangrijk zijn kom je ze tegen.
1: Hoeken, hoeken meten, driehoeken
Een hoek wordt bepaald door twee benen: (afb.1)
(afb.1)
Om een hoek te meten verdelen we die in graden.
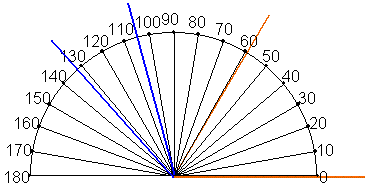
Een cirkel kunnen zo we verdelen in 360 "partjes" van 1 graad: (afb.2)
(afb.2)
Hoeveel graden een hoek bedraagt kun je meten met een gradenboog, die ook op je geodriehoek staat.
De hoek tussen de rode benen hieronder is 59 graden (59°), er passen 59 partjes van 1° tussen.
Tussen de blauwe benen hieronder is de hoek 27 graden (27°).
 (afb.3) (bron:wisfaq)
(afb.3) (bron:wisfaq)
Als het drie uur is, is er een hoek van 90° tussen de kleine en grote wijzer.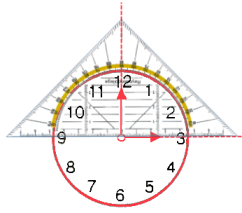 (afb.4)
(afb.4)
Zo'n hoek van 90° noemen we een "rechte hoek".
In een tekening duiden we zo'n rechte hoek vaak aan met twee haakse lijntjes : (afb.5)
(afb.5)
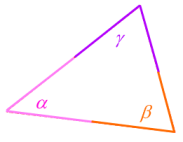
Driehoeken heten zo omdat ze drie hoeken hebben (duhh).
 (afb.6)
(afb.6)
Die hoeken geven we meestal aan met Griekse letters,
hier alfa (α) , beta (β) en gamma (γ) .
Feit: De drie hoeken van een driehoek zijn samen altijd 180°.
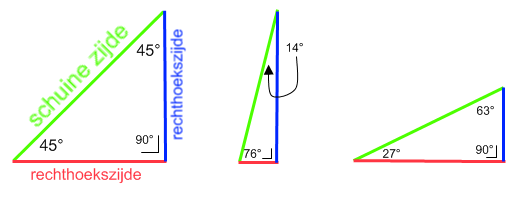
Een driehoek met een rechte hoek noemen we een rechthoekige driehoek .
Feit: In een rechthoekige driehoek is altijd één hoek bekend: die van 90°.
De andere twee hoeken van je rechthoekige driehoek zijn samen dus altijd 90°. Dit kunnen bijvoorbeeld twee hoeken van 45° zijn. Of het kan, zoals je in het plaatje hieronder ziet, ook anders:
 (afb.7)
(afb.7)
En nu komt het:
Sinus, cosinus en tangens geven de verhoudingen van de lengtes van de zijdes van rechthoekige driehoeken.
Er bestaat een verband tussen de hoeken van een rechthoekige driehoek en de lengte van de zijdes.
Dus als je een hoek hebt kan je daarmee berekenen hoelang de zijdes zijn.
Als je weet hoe lang de zijdes zijn kan je daarmee de grootte van de hoeken berekenen.
Je zou het ook met een gradenboog of liniaal kunnen doen, maar dit is preciezer en het is sneller.
(hoe cool is dat )
)
Bij deze cursus zijn ook een aantal oefenopgaven gemaakt, deze vind je onder de cursus.
Als je van deze cursus gebruik maakt, willen we je vriendelijk vragen te laten weten wat je er van vond:
- Geef eventuele foutjes aan;
- Zijn de onderdelen soms onduidelijk, of net erg helder?
- Ontbreken er volgens jou stukken, of heb je suggesties?
- ...
---------------------------------------------------------------------------------------
[microcursus] Goniometrie: sinus, cosinus en tangens (basis)
Auteurs: StrangeQuark , TD , Jan van de Velde
Inhoudsopgave
- Inleiding
- 1: Hoeken, hoeken meten, driehoeken
- 2: Aanliggende en overstaande rechthoekszijde
- 3: Verhoudingen: tangens, sinus en cosinus
- 4: Toepassen: met een hoek en een zijde een andere zijde berekenen
- 5: Toepassen: met twee zijdes een hoek berekenen
- 6: Eenheidscirkel
- 6.1 Hoeken in de goniometrische eenheidscirkel
- 6.2 Sinus en cosinus in de eenheidscirkel
- 6.3 Tangens in de eenheidscirkel
- 6.4 Goniometrische getallen op de eenheidscirkel
- 6.5 Goniometrische getallen en de "sinusvormige grafiek"
- 7: Goniometrie zonder rekenmachine
- 7.1 Grafisch én rekenen
- 7.2 Grafisch zónder rekenen: sinus en cosinus
- 7.3 Grafisch zónder rekenen: tangens
- (oefenopgaven)
Wat is goniometrie? Het woord goniometrie komt van het Oudgriekse woord γωνία (goonia) dat "hoek" betekent.
Sinus, cosinus en tangens zijn wiskundige gereedschappen om met hoeken te werken. Je komt ze overal in natuurkunde en techniek tegen. Bij het bouwen van bruggen en huizen, spiegels en lenzen, samenstellen en ontbinden van krachten, bij alle vormen van radiocommunicatie, bij radar, in je computer. Kortom, overal waar hoeken belangrijk zijn kom je ze tegen.
1: Hoeken, hoeken meten, driehoeken
Een hoek wordt bepaald door twee benen:
 (afb.1)
(afb.1)Om een hoek te meten verdelen we die in graden.
Een cirkel kunnen zo we verdelen in 360 "partjes" van 1 graad:
 (afb.2)
(afb.2)Hoeveel graden een hoek bedraagt kun je meten met een gradenboog, die ook op je geodriehoek staat.
De hoek tussen de rode benen hieronder is 59 graden (59°), er passen 59 partjes van 1° tussen.
Tussen de blauwe benen hieronder is de hoek 27 graden (27°).
 (afb.3) (bron:wisfaq)
(afb.3) (bron:wisfaq)Als het drie uur is, is er een hoek van 90° tussen de kleine en grote wijzer.
 (afb.4)
(afb.4)Zo'n hoek van 90° noemen we een "rechte hoek".
In een tekening duiden we zo'n rechte hoek vaak aan met twee haakse lijntjes :
 (afb.5)
(afb.5)Driehoeken heten zo omdat ze drie hoeken hebben (duhh).
 (afb.6)
(afb.6)Die hoeken geven we meestal aan met Griekse letters,
hier alfa (α) , beta (β) en gamma (γ) .
Feit: De drie hoeken van een driehoek zijn samen altijd 180°.
Een driehoek met een rechte hoek noemen we een rechthoekige driehoek .
Feit: In een rechthoekige driehoek is altijd één hoek bekend: die van 90°.
De andere twee hoeken van je rechthoekige driehoek zijn samen dus altijd 90°. Dit kunnen bijvoorbeeld twee hoeken van 45° zijn. Of het kan, zoals je in het plaatje hieronder ziet, ook anders:
 (afb.7)
(afb.7)En nu komt het:
Sinus, cosinus en tangens geven de verhoudingen van de lengtes van de zijdes van rechthoekige driehoeken.
Er bestaat een verband tussen de hoeken van een rechthoekige driehoek en de lengte van de zijdes.
Dus als je een hoek hebt kan je daarmee berekenen hoelang de zijdes zijn.
Als je weet hoe lang de zijdes zijn kan je daarmee de grootte van de hoeken berekenen.
Je zou het ook met een gradenboog of liniaal kunnen doen, maar dit is preciezer en het is sneller.
(hoe cool is dat
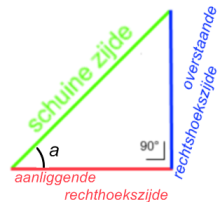 (afb.8)
(afb.8) (afb.9)
(afb.9)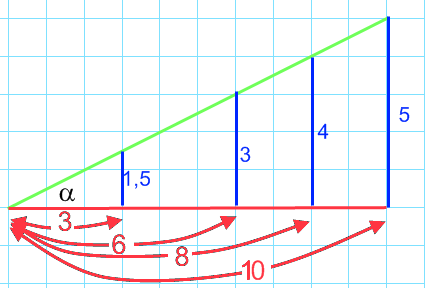 (afb.10)
(afb.10)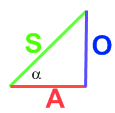 (afb.11)
(afb.11)
 (afb.12,13) .....Wat ik onthou is: S
(afb.12,13) .....Wat ik onthou is: S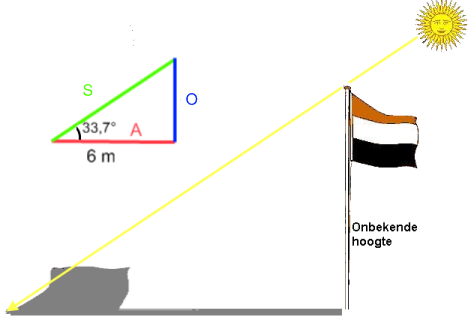 (afb.14)
(afb.14) (afb.15)
(afb.15)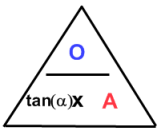 (afb.16)
(afb.16) (afb.17)
(afb.17) (afb.18)
(afb.18) (afb.19)
(afb.19)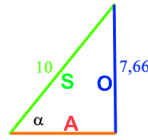 (afb.20)
(afb.20)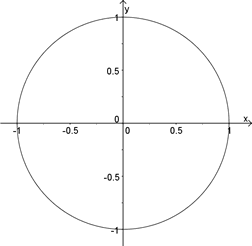 (afb.21)
(afb.21)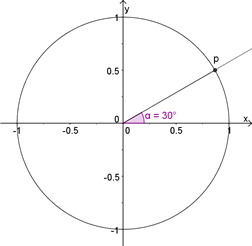 (afb.22)
(afb.22)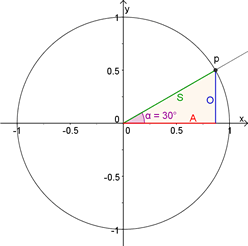 (afb.23)
(afb.23)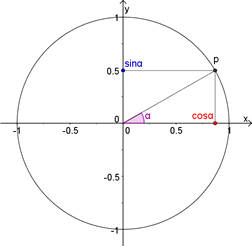 (afb.24)
(afb.24)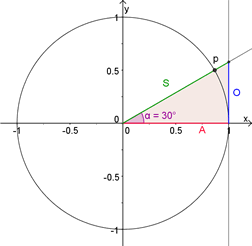 (afb.25)
(afb.25)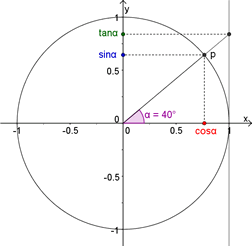 (afb.26)
(afb.26)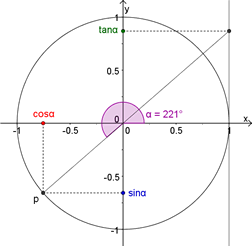 (afb.27)
(afb.27)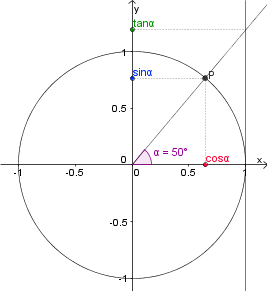 (afb.28)
(afb.28) (afb.29)
(afb.29)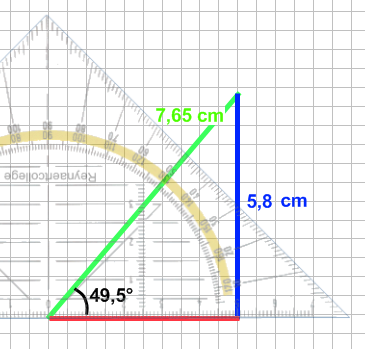 (afb.30)
(afb.30)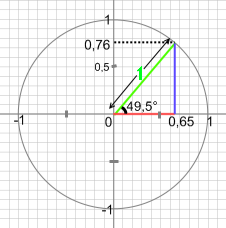 (afb.31)
(afb.31)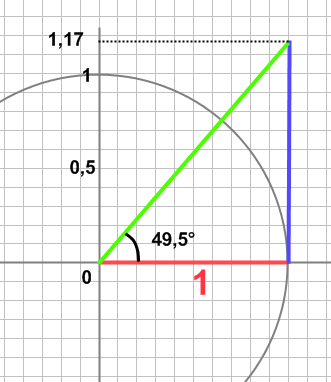 (afb.32)
(afb.32)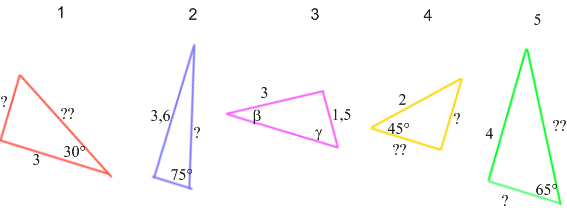 (afb.1)
(afb.1) (afb.2)
(afb.2)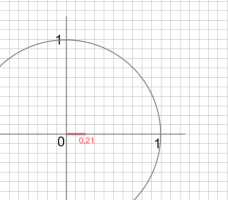 (afb.3)
(afb.3)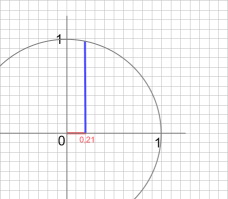 (afb.4)
(afb.4)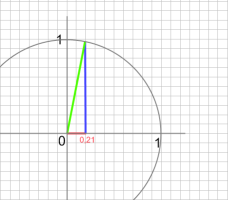 (afb.5)
(afb.5)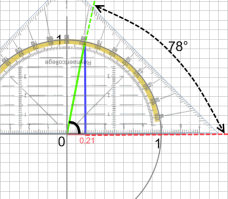 (afb.6)
(afb.6)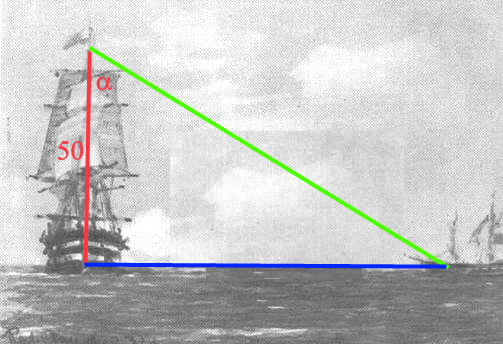 (afb.7)
(afb.7)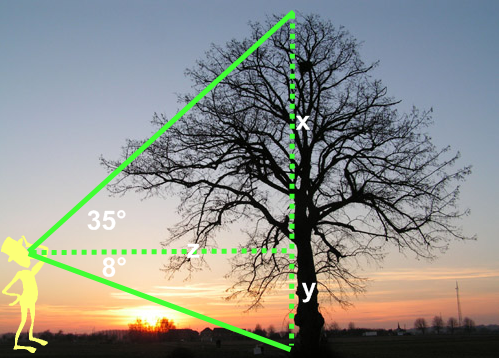 (afb.8)
(afb.8)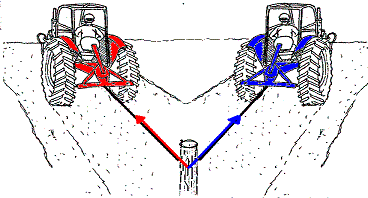 (afb.9)
(afb.9)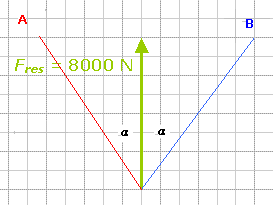 (afb.10)
(afb.10)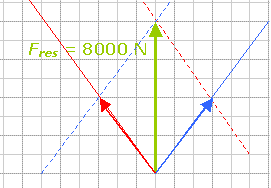 (afb.11)
(afb.11)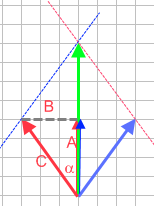 (afb.12)
(afb.12)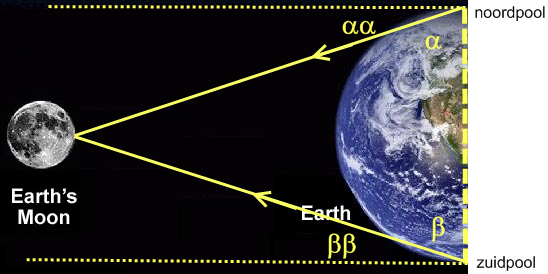 (afb.13)
(afb.13)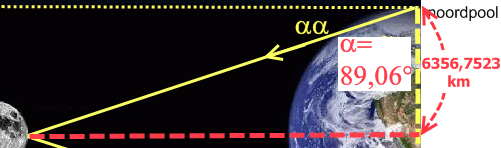 (afb.14)
(afb.14)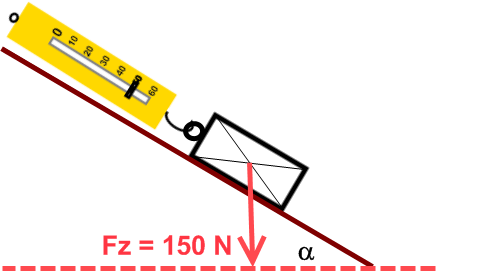 (afb.15)
(afb.15)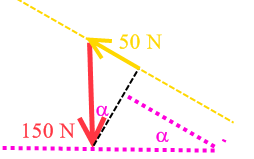 (afb.16)
(afb.16)