Ik vind het niet direct maar daar komt het op neer:
http://galileo.phys.virginia.edu/classes/152.mf1i.spring02/GravField.htm
Field
Inside a Spherical Shell

This turns out to be surprisingly simple! We imagine the shell to be very thin, with a mass density
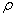
kg per square meter of surface. Begin by drawing a two-way cone radiating out from the point
P, so that it includes two small areas of the shell on opposite sides: these two areas will exert gravitational attraction on a mass at
P in opposite directions. It turns out that they exactly
cancel.
This is because the ratio of the areas
A1 and
A2 at distances
r1 and
r2 are given by
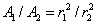
: since the cones have the same angle, if one cone has twice the height of the other, its base will have twice the diameter, and therefore
four times the area. Since the masses of the bits of the shell are proportional to the areas, the ratio of the masses of the cone bases is also
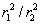
. But the gravitational attraction at
P from these masses goes as
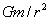
, and that
r2 term
cancels the one in the areas, so the two opposite areas have equal and opposite gravitational forces at
P.
In fact, the gravitational pull from every small part of the shell is balanced by a part on the opposite side—you just have to construct a lot of cones going through
P to see this. (There is one slightly tricky point—the line from
P to the sphere’s surface will in general cut the surface at an angle. However, it will cut the opposite bit of sphere
at the same angle, because any line passing through a sphere hits the two surfaces at the same angle, so the effects balance, and the base areas of the two opposite small cones are
still in the ratio of the squares of the distances
r1,
r2.)
Die oppervlaktes die Area A1 en A2 zijn vlakke cirkels, en daar ben ik niet akkoord mee, het moeten
bolkappen zijn , duidelijk toch?
Klik op de pagina's, dan opent hij een nieuw venster met afbeelding... Rechtsklikken eigenschappen voor link












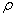 kg per square meter of surface. Begin by drawing a two-way cone radiating out from the point P, so that it includes two small areas of the shell on opposite sides: these two areas will exert gravitational attraction on a mass at P in opposite directions. It turns out that they exactly cancel.
kg per square meter of surface. Begin by drawing a two-way cone radiating out from the point P, so that it includes two small areas of the shell on opposite sides: these two areas will exert gravitational attraction on a mass at P in opposite directions. It turns out that they exactly cancel. 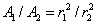 : since the cones have the same angle, if one cone has twice the height of the other, its base will have twice the diameter, and therefore four times the area. Since the masses of the bits of the shell are proportional to the areas, the ratio of the masses of the cone bases is also
: since the cones have the same angle, if one cone has twice the height of the other, its base will have twice the diameter, and therefore four times the area. Since the masses of the bits of the shell are proportional to the areas, the ratio of the masses of the cone bases is also 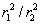 . But the gravitational attraction at P from these masses goes as
. But the gravitational attraction at P from these masses goes as 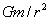 , and that r2 term cancels the one in the areas, so the two opposite areas have equal and opposite gravitational forces at P.
, and that r2 term cancels the one in the areas, so the two opposite areas have equal and opposite gravitational forces at P. 