Tweede afgeleide van kinetische energie

[anusthesist]

De laatste tijd ben ik me meer gaan verdiepen in hoe je bepaalde formules kunt beredeneren uit andere formules.

Zo kwam ik erachter (ik weet het, voor velen hier vrij evident, maar op het gebied van natuurkunde en dan wat dieper erop in gaan zonder domweg formules te stampen ben ik best een leek) dat de eerste afgeleide tot impuls leidt. De bekende formule E = 1/2mv2 wordt als je differentieert mv.

Nu vraag ik me af of ik goed zit met betrekking tot de tweede afgeleide als functie van tijd:

De verandering van de snelheid als functie van tijd levert dv/dt op. dv/dt ken ik als de formule voor versnelling of acceleratie (a). Als we dit invullen in de formule P = mv krijgen we m(dv/dt) ofwel ma. Kan ik zo stellen dat je dan kracht (F) krijgt alszijnde de verandering van impuls als functie van tijd (F=ma)?

Bvd

[Anton_v_U]

Goed gezien. Verandering van impuls per tijdseenheid is de (netto) kracht. Kracht maal tijd F.dt is krachtstoot = verandering van impuls: F.dt = dp. Dus impulsverandering per tijdseenheid dp/dt = F.dt/dt = F is een kracht.

[aadkr]

de mssaimpuls van een voorwerp is:

\(\vec{p}=m \cdot \vec{v}\)

\(\vec{F}=\frac{d\vec{p}}{dt}\)

\(\vec{F}=\frac{d(m\cdot \vec{v})}{dt}\)

\(\vec{F}=\frac{dm}{dt} \cdot \vec{v}+m \cdot \frac{d\vec{v}}{dt}\)

[anusthesist]

Goed gezien. Verandering van impuls per tijdseenheid is de (netto) kracht. Kracht maal tijd F.dt is krachtstoot = verandering van impuls: F.dt = dp. Dus impulsverandering per tijdseenheid dp/dt = F.dt/dt = F is een kracht.

Dank voor je antwoord. Ik heb nogal moeite dit voor me te zien als een grafische weergave.

E=1/2mv2 levert een hyperbool op. De impuls is dan een lineaire raaklijn. Hoe verhoudt zich dan de grafische functie van F zich tot de al lineaire raaklijn P (=mv)?

Ik hoop dat je een beetje begrijpt wat ik bedoel...met andere woorden, hoe ziet de grafiek van F=ma eruit in verhouding tot P=mv? Vaak zegt een grafiek meer dan 1000 woorden, maar helaas heb ik geen mooi programmaatje om de variabelen in te vullen om een grafische weergave te krijgen.

[mathfreak]

Dank voor je antwoord. Ik heb nogal moeite dit voor me te zien als een grafische weergave.

E=1/2mv² levert een hyperbool op.

Nee, dit levert als functie van v een parabool op. Ga dit desnoods voor jezelf na door iets over tweedegraadsfuncties en de bijbehorende grafieken op te zoeken.
 
Bedenk dat F in feite samenhangt met de afgeleide van v naar t volgens

\(F=m\frac{dv}{dt}\)

dus F∙dt = m∙dv, dus

\(v=\int\frac{F}{m}dt\)

, dus v stelt als het ware de primitieve van F voor. Hier valt niet direct eeen grafische voorstelling bij te bedenken, tenzij je weet hoe F als functie van t afhangt.
 

[anusthesist]

Sorry, bedoelde uiteraard een parabool, stom van me. De terminologie is nogal lang geleden voor mij

Maar de vraag blijft staan, dus dank voor je antwoord.

[317070]

hoe ziet de grafiek van F=ma eruit in verhouding tot P=mv?

Wel, de versnelling a is de afgeleide van de snelheid v naar de tijd, dus de kracht F is de afgeleide van de impuls P naar de tijd.
 
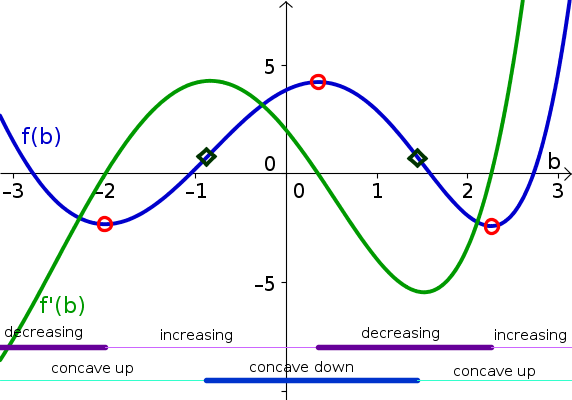
Als je dus een grafiek hebt van de impuls P naar de tijd, dan geeft de grafiek van de kracht F aan hoe steil die grafiek van P is op ieder tijdstip.
 
Zie bijvoorbeeld hieronder. De horizontale as is de tijd, dan zou de blauwe grafiek de impuls op een object door de tijd kunnen voorstellen, en de groene de totale kracht op dat object door de tijd.
 
Iedere keer als de grafiek van de impuls een extremum bereikt (en dus minimaal of maximaal is), is zijn afgeleide 0. De totale kracht F is dus op dat tijdstip ook nul.
 

[Flisk]

De bekende formule E = 1/2mv2 wordt als je differentieert mv.

Nu vraag ik me af of ik goed zit met betrekking tot de tweede afgeleide als functie van tijd:

Als je de kinetische energie differentieert naar de snelheid krijg je

\(mv\)

Maar als je differentieert naar de tijd krijg je iets anders:

\(\frac{\text{d}}{\text{d}t}(\frac{1}{2}mv^2)=mv\frac{\text{d}}{\text{d}t}v=mva\)

Wat dus niet direct iets nuttig/zinnig voorstelt. 

 

Kan ik zo stellen dat je dan kracht (F) krijgt alszijnde de verandering van impuls als functie van tijd (F=ma)?

Als de massa constant blijft klopt dit ja, dat is de tweede wet van Newton.

Maar F is dus niet de tweede afgeleide i.f.v. de tijd van de kinetische energie. F is, indien constante massa wordt verondersteld, de eerste afgeleide naar de tijd van impuls.

 

Hoe ziet de grafiek van F=ma eruit in verhouding tot P=mv? Vaak zegt een grafiek meer dan 1000 woorden, maar helaas heb ik geen mooi programmaatje om de variabelen in te vullen om een grafische weergave te krijgen.

Daar is niets speciaal aan hoor. Plot een willekeurige grafiek van een functie samen met de afgeleide van die functie en je krijgt een idee van hoe P(t) eruit ziet t.o.v. F(t).

[anusthesist]

Wel, de versnelling a is de afgeleide van de snelheid v naar de tijd, dus de kracht F is de afgeleide van de impuls P naar de tijd.

 

Als je dus een grafiek hebt van de impuls P naar de tijd, dan geeft de grafiek van de kracht F aan hoe steil die grafiek van P is op ieder tijdstip.

 

Zie bijvoorbeeld hieronder. De horizontale as is de tijd, dan zou de blauwe grafiek de impuls op een object door de tijd kunnen voorstellen, en de groene de totale kracht op dat object door de tijd.

 

Iedere keer als de grafiek van de impuls een extremum bereikt (en dus minimaal of maximaal is), is zijn afgeleide 0. De totale kracht F is dus op dat tijdstip ook nul.

 

Top, dank je, hier was ik op zoek naar inderdaad. Klinkt vrij logisch zoals je het zegt en wat de grafiek laat zien. Mijn vraag is denk ik wel beantwoord nu

Eén ding waar ik nog een beetje tegenaan loop is de kracht (F) destilleren uit de Lagrangian van kinetische energie minus de potentiële energie (had nog nooit van Lagrangian gehoord totdat ik me dus meer begon te verdiepen in deze materie). Dat vind ik nog vrij complex, maar daar zijn wel youtube-filmpjes over dus die ga ik nog eens goed bestuderen.

In ieder geval bedankt voor je uitleg!