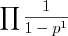@Th.B: Ik snap dit niet. Bedoel je dan het specifieke geval dat s = 1? Bedoel je dat
\(\prod \frac{1}{1-p^{1}}\)
door een aantal ‘trucjes’ uit te halen kan worden herschreven als:
\(\prod \frac{p-1}{p}\)
?
Een product dat 0 is klinkt mij ook nogal vreemd in de oren. Dit zou moeten betekenen dat er een factor 0 voorkomt in het product, maar hoe kan zo'n factor nu ooit ontstaan?
@Safe: p is inderdaad een priemgetal. Als je daar grenzen aan wilt stellen: Het viel me op dat het product van alle priemgetallen onder wortel(n) vermenigvuldigd met n ongeveer het aantal priemgetallen tot n is. En dat het verschil tussen die uitkomst en het werkelijke aantal priemgetallen dan ongeveer gelijk is aan het priemgetallen tot wortel(n).
althans tot n = 100.000 lijkt het ongeveer wel te kloppen. Maar ook weer niet helemaal. En ik snap niet hoe dat nu komt dus hopelijk heeft iemand dit ooit al eens onderzocht.