We moet het domein, bereik, asymtoten en het nulpunt van een logaritmische functie kunnen bepalen, echter ik weet alleen niet hoe.
Een voorbeeld van zo een vraag is:
Geef het domein, bereik, vergelijking van de asysmto(o)t(en) en het nulpunt
a. f(x) = 3 + 3log(8-2x)
kan iemand me helpen hoe ik dit moet aanpakken
alvast, bedankt
Forumregels
(Middelbare) school-achtige vragen naar het forum "Huiswerk en Practica" a.u.b.
Zie eerst de Huiswerkbijsluiter
(Middelbare) school-achtige vragen naar het forum "Huiswerk en Practica" a.u.b.
Zie eerst de Huiswerkbijsluiter
- Jaap Huizen
- Artikelen: 0
- Berichten: 7
- Lid geworden op: di 08 dec 2015, 17:03
- mathfreak
- Pluimdrager
- Artikelen: 0
- Berichten: 3.505
- Lid geworden op: zo 28 dec 2008, 16:22
Re: domein, bereik, asymtoten en het nulpunt van een logaritme
Het domein bevat alle toegestane waarden van x, dus voor welke waarden van x bestaat 3log(8-2x)?
Het bereik bevat alle mogelijke functiewaarden, dus wat wordt hier het bereik?
De asymptoot vind je door die waarde van x waarvoor 3log(8-2x) niet gedefinieerd is en het nulpunt vind je door de vergelijking
f(x) = 0 op te lossen. Wat wordt dus de vergelijking van de asymptoot en wat is het gevraagde nulpunt?
Het bereik bevat alle mogelijke functiewaarden, dus wat wordt hier het bereik?
De asymptoot vind je door die waarde van x waarvoor 3log(8-2x) niet gedefinieerd is en het nulpunt vind je door de vergelijking
f(x) = 0 op te lossen. Wat wordt dus de vergelijking van de asymptoot en wat is het gevraagde nulpunt?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
- Jaap Huizen
- Artikelen: 0
- Berichten: 7
- Lid geworden op: di 08 dec 2015, 17:03
Re: domein, bereik, asymtoten en het nulpunt van een logaritme
Bedankt mathfreak dit is mijn uitwerking dan
Domein:
De logaritme log(a) is alleen gedefinieerd voor a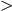 0 dus dan moet 8-2x > 0, -2x > -8, x > 4
0 dus dan moet 8-2x > 0, -2x > -8, x > 4
Bereik:
?
Asymtoot:
Zou dit dan 4 zijn?
Nulpunt:
3log(8-2x)= 0
8-2x=3^0
8-2x=1
-2x=-7
x=3,5
moet er ook een y-waarde bij het nulpunt? en hoe bereken ik die?
Domein:
De logaritme log(a) is alleen gedefinieerd voor a
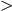 0 dus dan moet 8-2x > 0, -2x > -8, x > 4
0 dus dan moet 8-2x > 0, -2x > -8, x > 4Bereik:
?
Asymtoot:
Zou dit dan 4 zijn?
Nulpunt:
3log(8-2x)= 0
8-2x=3^0
8-2x=1
-2x=-7
x=3,5
moet er ook een y-waarde bij het nulpunt? en hoe bereken ik die?
- mathfreak
- Pluimdrager
- Artikelen: 0
- Berichten: 3.505
- Lid geworden op: zo 28 dec 2008, 16:22
Re: domein, bereik, asymtoten en het nulpunt van een logaritme
x>4 is niet juist, want dan geldt: 8-2x<0, wat een logaritme van een negatief getal geeft. Dit is echter niet mogelijk. Wat gebeurt er met het ongelijkheidsteken als je een ongelijkheid door een negatief getal deelt? Wat moet er hier dus gelden voor x, dus wat is je domein?De logaritme log(a) is alleen gedefinieerd voor achar3E.png0 dus dan moet 8-2x > 0, -2x > -8, x > 4
Als 3log(8-2x) bestaat, welke waarden kan deze logaritme dan allemaal aannemen? Wat wordt dus het bereik?Bereik:
?
Een asymptoot wordt weergegeven als de vergelijking van een lijn. Wat is die vergelijking in dit geval?Asymptoot:
Zou dit dan 4 zijn?
Nee, het nulpunt van een functie f is per definitie die waarde van x waarvoor f(x) = 0.Nulpunt:
3log(8-2x)= 0
8-2x=3^0
8-2x=1
-2x=-7
x=3,5
moet er ook een y-waarde bij het nulpunt?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
- Jaap Huizen
- Artikelen: 0
- Berichten: 7
- Lid geworden op: di 08 dec 2015, 17:03
Re: domein, bereik, asymtoten en het nulpunt van een logaritme
Is dit wel goeie antwoord dan?
Domein:
Ooh het domein is dan x<4
Bereik:
Alles is mogelijk
Asymtoot:
8-2x=0
-2x=-8
x=4
Nulpunt:
f(x)=3+3log(8-2x)
3+3log(8-2x)=0
3log(8-2x)=-3
8-2x = 3-3 = 1/27
2x = 8-1/27 = 215/27
x = 215/54
Domein:
Ooh het domein is dan x<4
Bereik:
Alles is mogelijk
Asymtoot:
8-2x=0
-2x=-8
x=4
Nulpunt:
f(x)=3+3log(8-2x)
3+3log(8-2x)=0
3log(8-2x)=-3
8-2x = 3-3 = 1/27
2x = 8-1/27 = 215/27
x = 215/54
- mathfreak
- Pluimdrager
- Artikelen: 0
- Berichten: 3.505
- Lid geworden op: zo 28 dec 2008, 16:22
Re: domein, bereik, asymtoten en het nulpunt van een logaritme
Dat klopt. Je kunt dit ook noteren met de intervalnotatieDomein:
Ooh het domein is dan x<4
\(\langle\rightarrow,4\rangle\)
Dat klopt. Je kunt dit ook noteren met de notatieBereik:
Alles is mogelijk
\(\rr\)
De asymptoot (let op de schrijfwijze) is inderdaad de lijn x = 4.Asymptoot:
8-2x=0
-2x=-8
x=4
Dat klopt. Merk op dat je ook kunt schrijven datNulpunt:
f(x)=3+3log(8-2x)
3+3log(8-2x)=0
3log(8-2x)=-3
8-2x = 3-3 = 1/27
2x = 8-1/27 = 215/27
x = 215/54
\(x=4-\frac{1}{54}=3 \frac{53}{54}\)
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
- Safe
- Pluimdrager
- Artikelen: 0
- Berichten: 10.058
- Lid geworden op: wo 17 nov 2004, 12:37
Re: domein, bereik, asymtoten en het nulpunt van een logaritme
Jaap Huizen schreef: -2x > -8, x > 4
Wat doe je hier ...
Bv: -8<-2 (klopt dit?)
Deel nu links en rechts door -2 ...