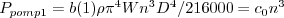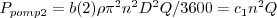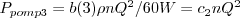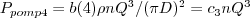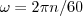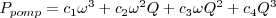QuoteHeb je al een formule voor het verband tussen het debiet Q (of de stroomsnelheid v) en de hoeksnelheid ω van de pomp?
Geloof het wel:
% Vermogen.
P = b(1) .* psi * phi + ...
b(2) .* psi .* Q + ...
b(3) .* psi ./ phi .* Q.^2 + ...
b(4) .* psi ./ phi.^2 .* Q.^3;
met:
an2 = pi .* n / 60 .* Dimp;
psi = rho_i .* an2.^2;
phi = pi .* Wimp .* Dimp .* an2;
Mits er sprake is van een constante dichtheid dus.
Met de gedachte dat
Dit wordt bevestigd door een proefschrift waarin C1-4 constanten zijn zoals hierboven in het stukje code ook vermeld:
Maar dit is wel bruikbaar denk ik? Zal alleen een grote wirwar van verbindingen worden in de simulatie omdat alles van elkaar afhangt grrr
p.s. Hoe kwam je tot deze afgeleide:
\(P_{ver} \, = \, \frac{\mbox{d} \left ( \frac{1}{2} \, \mbox{I} \, \omega^2 \right )}{\mbox{d}t}\)
\(P_{ver} \, = \, \mbox{I} \, \omega \, \dot{\omega}\)