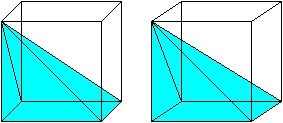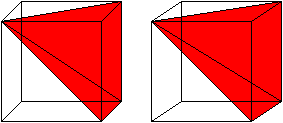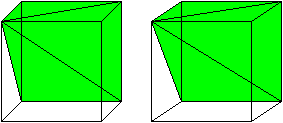
https://en.m.wikipedia.org/wiki/Method_of_exhaustion
Onder propositie 10 lees ik het volgende:
''The volume of a cone is a third of the volume of the corresponding cylinder which has the same base and height''
Nu was ik benieuwd of ik het zelf kon 'bewijzen' of althans redeneren, want als ik kijk in het wiki-artikel over 'de kegel' dan gooien ze mij allemaal integralen om de oren en de eerlijkheid gebiedt te zeggen: dat is nooit mijn sterkste punt geweest.
Dus ik ging even nadenken en kwam met het volgende:
1) Een kegel kun je beschouwen als allemaal driehoeken naast elkaar totdat ze een volledige cirkel hebben afgelegd.
2) De oppervlakte van een driehoek = (lengte L * breedte B)/2 = Adriehoek
3) De omtrek van een cirkel, uitgedrukt in radialen = 2π
4) Als je dit combineert krijg je voor het volume van een kegel 2π(LB/2).
5) De 2'en strepen we tegen elkaar weg dus vereenvoudigd krijgen we π*L*B = volume kegel
Als ik dit verifiëer is het -tot mijn grote verbazing eerlijk gezegd
Het antwoord moge wel goed zijn, maar is de gedachtegang ook goed?
Bij voorbaat dank!
-edit- nee dus...shoot!
Het werkt blijkbaar alleen met een driehoek met rechte zijdes 3 en 4 met schuine zijde 5.
Dan is mijn vraag: waarom werkt het wél voor deze maten maar niet voor andere?
Mijn extra dank!