Voor de goede orde, dit had ik dus in gedachten:
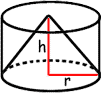
Dan zien jullie dus ook meteen 'de driehoek' die ik in gedachten had, in het geval het niet duidelijk was uit mijn verhaal.

anusthesist schreef:Ik snap dat schetsje niet...lijkt wel een tekening van Escher
Nee - dat wordt zeer klein (infinitesimaal) genomen waardoor je de kromming van het buitenvlak mag verwaarlozen. Ik heb het groot getekend omdat je anders niet ziet wat er gebeurt.anusthesist schreef:De lengte van het stukje taartpunt dat op de cirkel ligt is dan 1rad?