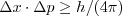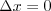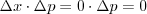Met de onbepaaldheidsrelatie (OR) wordt de plaats-impuls-relatie bedoeld in de vorm
\(\Delta x\cdot\Delta p\geq h/(4\pi)\)
; de "statistische" relatie \(\sigma_x\cdot\sigma_p\geq h/(4\pi)\)
staat niet in het examenprogramma vwo.De leerling verkrijgt voor een goed antwoord twee scorepunten. Volgens het officiële correctievoorschrift waarmee een docent zoals ik het antwoord van een leerling moet beoordelen, wordt er 1 scorepunt toegekend voor "inzicht dat 'stilstaan' betekent dat
\(\Delta p=0\)
en/of \(\Delta x=0\)
". (Het andere scorepunt is voor "gebruik van de onbepaaldheidsrelatie van Heisenberg en conclusie".)Uitlegmogelijkheid 1, met
\(\Delta p=0\)
, kan volgens mij zijn: "Stel dat H stilstaat, dan is \(p=0\)
, dus \(\Delta p=0\)
. Omdat H zich binnen het HI-molecuul bevindt (afgezien van tunneling), is \(\Delta x\)
eindig. \(\Delta x\cdot\Delta p=\text{eindig}\cdot0=0\)
is in strijd met de OR, dus kan H niet stilstaan." Tot zover geen probleem; op het niveau van het vwo lijkt me dit goed. (Graag commentaar als deze uitleg niet goed is.)De vermelding "en/of
\(\Delta x=0\)
" in het correctievoorschrift suggereert echter dat de vraag ook kan worden beantwoord via \(\Delta x=0\)
. Bij voorbeeld: "Als we de plaats van H twee maal meten en we vinden op beide momenten dezelfde waarde voor x, dan is \(\Delta x=0\)
, dus staat H stil. Maar dit schendt de OR want \(\Delta x\cdot\Delta p=0\cdot\Delta p=0\)
" Hiermee heb ik een probleem. In deze uitleg is \(\Delta x\)
een verschil tussen twee opeenvolgende metingen van \(x\)
-- maar dat is toch wezenlijk iets anders dan de onbepaaldheid waarover de OR gaat?Een andere uitleg met
\(\Delta x=0\)
zou kunnen luiden "Stel dat H stilstaat, dan is \(\Delta x=0\)
, in strijd met de OR." Dit lijkt me ook onjuist, want als ik weet dat iets stilstaat, weet ik niet noodzakelijk wáár het stilstaat. Voorbeeld: als ik nul dopplerverschuiving meet in het licht van een laserbron, weet ik nog niet wáár de bron stilstaat, zodat \(\Delta x\)
zeer groot is.Mijn vraag: is een kwantummechanisch juiste uitleg bij vraag 20 mogelijk via
\(\Delta x=0\)
? Zo ja, welke uitleg?