Botssnelheid
Moderator: physicalattraction
-
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Botssnelheid
Met welke snelheid botsen auto A en B frontaal terwijl ze beide 50 km/u rijden?
- dannypje
- Artikelen: 0
- Berichten: 768
- Lid geworden op: zo 27 mei 2012, 20:30
Re: Botssnelheid
Dat zal ongeveer 400 km/u zijn.
In the beginning, there was nothing. Then he said:"Light". There was still nothing but you could see it a whole lot better now.
-
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Re: Botssnelheid
De vraag heb ik niet volledig geformuleerd.
Wat is de frontale botssnelheid van gelijke auto A en B met snelheid is 50 km/u?
Filosofische benadering:
Voor auto A geldt: Rijdt in heenrichting met snelheid is 50 km/u als botssnelheid.
Voor auto B geldt: Rijdt in terugrichting met snelheid is 50 km/u als botssnelheid.
Voor auto geldt: Rijdt met snelheid is 50 km/u als botssnelheid.
Voor beide auto’s geldt: Botssnelheid is 50 km/u.
Wat is de rekenkundige benadering?
Wat is de frontale botssnelheid van gelijke auto A en B met snelheid is 50 km/u?
Filosofische benadering:
Voor auto A geldt: Rijdt in heenrichting met snelheid is 50 km/u als botssnelheid.
Voor auto B geldt: Rijdt in terugrichting met snelheid is 50 km/u als botssnelheid.
Voor auto geldt: Rijdt met snelheid is 50 km/u als botssnelheid.
Voor beide auto’s geldt: Botssnelheid is 50 km/u.
Wat is de rekenkundige benadering?
- physicalattraction
- Moderator
- Artikelen: 0
- Berichten: 4.164
- Lid geworden op: do 30 mar 2006, 15:37
Re: Botssnelheid
Je hebt je vraag nog steeds niet volledig geformuleerd. Wat betekent botssnelheid bij jou?
- Jan van de Velde
- Moderator
- Artikelen: 0
- Berichten: 51.334
- Lid geworden op: di 11 okt 2005, 20:46
Re: Botssnelheid
Laat ik dat dan eens anders proberen.
Laat ik veronderstellen dat hier om reële auto's gaat.
Identieke auto's, gelijke snelheid, beide een prima kreukelzone die niet overvraagd wordt.
Ofwel, aan het eind van de botsing staan ze beide stil zonder teruggeveerd te zijn, zo ongeveer met de voorraamkozijnen tegen elkaar
Van elke auto is de snelheidsverandering bij de botsing van 50 naar 0 = 50 km/h.
zodra de bumpers raken staan die stil en blijven op dezelfde plek stilstaan. De kreukelzone veert in en de rest van de auto staat na een metertje ook stil.
En dat is dan precies evenveel als wanneer een zo'n auto tegen een betonblok gebotst zou zijn dat niet meegeeft. De kracht van gordels en airbags op de chauffeurs is ook even groot geweest als wanneer ze op dat betonblok gebotst zouden zijn, want hun botsweg (remweg = lengte kreukelzone) is even groot. Ook daar staat de bumper ogenblikkelijk stil terwijl de auto nog naar het betonblok toekreukelt.
Was dat dan jouw werkelijke vraag?
Laat ik veronderstellen dat hier om reële auto's gaat.
Identieke auto's, gelijke snelheid, beide een prima kreukelzone die niet overvraagd wordt.
Ofwel, aan het eind van de botsing staan ze beide stil zonder teruggeveerd te zijn, zo ongeveer met de voorraamkozijnen tegen elkaar
Van elke auto is de snelheidsverandering bij de botsing van 50 naar 0 = 50 km/h.
zodra de bumpers raken staan die stil en blijven op dezelfde plek stilstaan. De kreukelzone veert in en de rest van de auto staat na een metertje ook stil.
En dat is dan precies evenveel als wanneer een zo'n auto tegen een betonblok gebotst zou zijn dat niet meegeeft. De kracht van gordels en airbags op de chauffeurs is ook even groot geweest als wanneer ze op dat betonblok gebotst zouden zijn, want hun botsweg (remweg = lengte kreukelzone) is even groot. Ook daar staat de bumper ogenblikkelijk stil terwijl de auto nog naar het betonblok toekreukelt.
Was dat dan jouw werkelijke vraag?
ALS WIJ JE GEHOLPEN HEBBEN...
help ons dan eiwitten vouwen, en help mee ziekten als kanker en zo te bestrijden in de vrije tijd van je chip...
http://sciencetalk.nl/forumshowtopic=59270
help ons dan eiwitten vouwen, en help mee ziekten als kanker en zo te bestrijden in de vrije tijd van je chip...
http://sciencetalk.nl/forumshowtopic=59270
-
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Re: Botssnelheid
Niet echt.
Jouw uitkomst is een correct resultaat van associatief denken.
Een aantal jaren geleden is dat proefondervindelijk aangetoond op de TU Delft.
Had wel goedkoper gekund met onderstaande proef.
Alternatieve onderbouwing als resultaat van associatief denken.
1 Bevestig een bol boetseerklei aan een draad van 1 meter.
2 Bevestig de draad aan de wand van een muur.
3 Trek de bol horizontaal en laat het los.
4 Meet de vervorming van de bol.
5 Bevestig twee bollen boetseerklei elk aan een draad van 1 meter.
6 Knoop de uiteinden aan elkaar.
7 Trek beide bollen horizontaal en laat ze los.
8 Meet de vervorming van beide bollen.
9 Resultaat: Drie bollen met dezelfde vervorming.
10 Conclusie: Botssnelheid is 50 km/u.
De vervormingen van beide benaderingen zijn rekenkundig aan te tonen.
Het is en blijft dan ook een associatief denkresultaat dat rekenkundig is te toetsen.
Er ontbreekt (als rekenkundige benadering) een rekenresultaat in de zin van: Botssnelheid = snelheid A + / - snelheid B (km/u) of iets
dergelijks.
Ik hoop dat je hier wat mee kan.
Jouw uitkomst is een correct resultaat van associatief denken.
Een aantal jaren geleden is dat proefondervindelijk aangetoond op de TU Delft.
Had wel goedkoper gekund met onderstaande proef.
Alternatieve onderbouwing als resultaat van associatief denken.
1 Bevestig een bol boetseerklei aan een draad van 1 meter.
2 Bevestig de draad aan de wand van een muur.
3 Trek de bol horizontaal en laat het los.
4 Meet de vervorming van de bol.
5 Bevestig twee bollen boetseerklei elk aan een draad van 1 meter.
6 Knoop de uiteinden aan elkaar.
7 Trek beide bollen horizontaal en laat ze los.
8 Meet de vervorming van beide bollen.
9 Resultaat: Drie bollen met dezelfde vervorming.
10 Conclusie: Botssnelheid is 50 km/u.
De vervormingen van beide benaderingen zijn rekenkundig aan te tonen.
Het is en blijft dan ook een associatief denkresultaat dat rekenkundig is te toetsen.
Er ontbreekt (als rekenkundige benadering) een rekenresultaat in de zin van: Botssnelheid = snelheid A + / - snelheid B (km/u) of iets
dergelijks.
Ik hoop dat je hier wat mee kan.
- Jan van de Velde
- Moderator
- Artikelen: 0
- Berichten: 51.334
- Lid geworden op: di 11 okt 2005, 20:46
Re: Botssnelheid
ik begrijp niet wat je bezwaar is tegen dat "associatief denken" als het zoals je zegt rekenkundig aan te tonen is (en dat is het ook via de wet van behoud van impuls)
ALS WIJ JE GEHOLPEN HEBBEN...
help ons dan eiwitten vouwen, en help mee ziekten als kanker en zo te bestrijden in de vrije tijd van je chip...
http://sciencetalk.nl/forumshowtopic=59270
help ons dan eiwitten vouwen, en help mee ziekten als kanker en zo te bestrijden in de vrije tijd van je chip...
http://sciencetalk.nl/forumshowtopic=59270
-
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Re: Botssnelheid
Ik heb geen bezwaar tegen associatief denken.
De vraagstelling kan ook op onderstaande wijze worden geformuleerd.
Voor auto A geldt: Beweegt in heenrichting met snelheid is c als botssnelheid.
Voor auto B geldt: Beweegt in terugrichting met snelheid is c als botssnelheid.
Voor auto geldt: Beweegt met snelheid is c als botssnelheid.
Voor beide auto’s geldt: Botssnelheid is c (i.p.v. 2c).
Let op!
Het tegenovergestelde van botssnelheid (toenaderingssnelheid) is verwijderingssnelheid.
De vraagstelling kan dan ook op onderstaande wijze worden geformuleerd.
Voor foton A geldt: Beweegt in heenrichting met snelheid is c als verwijderingssnelheid.
Voor foton B geldt: Beweegt in terugrichting met snelheid is c als verwijderingssnelheid.
Voor foton geldt: Beweegt met snelheid is c als verwijderingssnelheid.
Voor beide fotonen geldt: Verwijderingssnelheid is c (i.p.v. 2c).
In wetenschapsforum is het onderwerp ‘Twee fotonen’ behandeld zonder resultaat.
In de discussie ‘Twee fotonen’ staat onderstaande formule m.b.t. optellen van snelheden centraal.
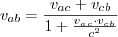
a en b fotonen, c, jij de waarnemer die ze wegschiet in tegenovergestelde richtingen
v_ab, de snelheid van a t.o.v. b wordt gevraagd
v_ac, de snelheid van een van de fotonen t.o.v. jou
v_cb, jouw snelheid t.o.v. het tweede foton.
Bedenk het volgende.
Voor stralingsgolf (gezien van buitenaf) geldt: Heeft wél een midden.
In de formule is c de waarnemer die zich in het midden waant (terwijl er niét een midden is).
Het is dan ook niet verwonderlijk dat de formule problemen oplevert.
Daarom zou het best eens kunnen dat vragen van bovenstaand kaliber uitsluitend van buitenaf gezien bekeken moeten te worden.
Terug naar de auto met 50 km/u.
Je kan de auto conform foton ook als stralingsgolf voorstellen die krimpt naar nul met 50 km/u.
Ook deze stralingsgolf (gezien van binnenuit) heeft niét een midden.
Het bevestigd dan ook mijn vermoeden dat associatief denken noodzakelijk is om de vraagstelling te beantwoorden.
De vraagstelling kan ook op onderstaande wijze worden geformuleerd.
- Wat is de frontale botssnelheid van massaloos auto A en B met snelheid is c.
Voor auto A geldt: Beweegt in heenrichting met snelheid is c als botssnelheid.
Voor auto B geldt: Beweegt in terugrichting met snelheid is c als botssnelheid.
Voor auto geldt: Beweegt met snelheid is c als botssnelheid.
Voor beide auto’s geldt: Botssnelheid is c (i.p.v. 2c).
Let op!
Het tegenovergestelde van botssnelheid (toenaderingssnelheid) is verwijderingssnelheid.
De vraagstelling kan dan ook op onderstaande wijze worden geformuleerd.
- Wat is de verwijderingssnelheid van foton A en B met snelheid is c.
Voor foton A geldt: Beweegt in heenrichting met snelheid is c als verwijderingssnelheid.
Voor foton B geldt: Beweegt in terugrichting met snelheid is c als verwijderingssnelheid.
Voor foton geldt: Beweegt met snelheid is c als verwijderingssnelheid.
Voor beide fotonen geldt: Verwijderingssnelheid is c (i.p.v. 2c).
In wetenschapsforum is het onderwerp ‘Twee fotonen’ behandeld zonder resultaat.
In de discussie ‘Twee fotonen’ staat onderstaande formule m.b.t. optellen van snelheden centraal.
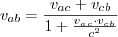
a en b fotonen, c, jij de waarnemer die ze wegschiet in tegenovergestelde richtingen
v_ab, de snelheid van a t.o.v. b wordt gevraagd
v_ac, de snelheid van een van de fotonen t.o.v. jou
v_cb, jouw snelheid t.o.v. het tweede foton.
Bedenk het volgende.
- Uiterste stralingsgrens foton (gezien van binnenuit) is het uiterste van heelal.
- Heelal dijt uit.
- Heelal heeft (gezien van binnenuit) niét een midden.
Voor stralingsgolf (gezien van buitenaf) geldt: Heeft wél een midden.
In de formule is c de waarnemer die zich in het midden waant (terwijl er niét een midden is).
Het is dan ook niet verwonderlijk dat de formule problemen oplevert.
Daarom zou het best eens kunnen dat vragen van bovenstaand kaliber uitsluitend van buitenaf gezien bekeken moeten te worden.
Terug naar de auto met 50 km/u.
Je kan de auto conform foton ook als stralingsgolf voorstellen die krimpt naar nul met 50 km/u.
Ook deze stralingsgolf (gezien van binnenuit) heeft niét een midden.
Het bevestigd dan ook mijn vermoeden dat associatief denken noodzakelijk is om de vraagstelling te beantwoorden.
- die hanze
- Artikelen: 0
- Berichten: 897
- Lid geworden op: wo 19 aug 2009, 00:19
Re: Botssnelheid
Zoals jan al aangaf: wat is in hemelsnaam associatief denken??
Wat betreft al jouw namen voor snelheid: "verwijderingsnelheid", "botssnelheid",... . Snelheid is gewoon een vector en een vector heeft coördinaten in een assenstelsel, verschillende waarnemers gebruiken verschillende assenstelsels en zo kunnen we over verschillende snelheden spreken als we telkens duidelijk aangeven wat het assenstelsel is dat we gebruiken.
Voor snelheden dicht bij de lichtsnelheid heeft men speciale relativieit nodig. Komt erop neer dat de ruimte niet euclidisch maar een minkowski metriek heeft waardoor een assenstelsels in elkaar transformeren via de lorentz-transformatie en die geeft inderdaad een andere niet intuïtieve optelling van snelheden. Dit gaat waarschijnlijk je pet te boven maar voor auto's aan 50 km/u zijn deze correctie's verwaarloosbaar klein.
In deze vraag gaat het vooral over wat de schade aan de auto/passagiers is. Dit is reeds eerder beantwoord en komt erop neer dat je moet kijken naar de acceleratie van de auto want het is versnelling dat (schijnkrachten) opwekt welke schadelijk kunnen zijn.
Wat betreft al jouw namen voor snelheid: "verwijderingsnelheid", "botssnelheid",... . Snelheid is gewoon een vector en een vector heeft coördinaten in een assenstelsel, verschillende waarnemers gebruiken verschillende assenstelsels en zo kunnen we over verschillende snelheden spreken als we telkens duidelijk aangeven wat het assenstelsel is dat we gebruiken.
Voor snelheden dicht bij de lichtsnelheid heeft men speciale relativieit nodig. Komt erop neer dat de ruimte niet euclidisch maar een minkowski metriek heeft waardoor een assenstelsels in elkaar transformeren via de lorentz-transformatie en die geeft inderdaad een andere niet intuïtieve optelling van snelheden. Dit gaat waarschijnlijk je pet te boven maar voor auto's aan 50 km/u zijn deze correctie's verwaarloosbaar klein.
In deze vraag gaat het vooral over wat de schade aan de auto/passagiers is. Dit is reeds eerder beantwoord en komt erop neer dat je moet kijken naar de acceleratie van de auto want het is versnelling dat (schijnkrachten) opwekt welke schadelijk kunnen zijn.
- Jan van de Velde
- Moderator
- Artikelen: 0
- Berichten: 51.334
- Lid geworden op: di 11 okt 2005, 20:46
Re: Botssnelheid
En dan bedoelen we verwaarloosbaar als in "pas tot uiting komend in de tig-ste decimaal na de komma".die hanze schreef: voor auto's aan 50 km/u zijn deze correctie's verwaarloosbaar klein.
ALS WIJ JE GEHOLPEN HEBBEN...
help ons dan eiwitten vouwen, en help mee ziekten als kanker en zo te bestrijden in de vrije tijd van je chip...
http://sciencetalk.nl/forumshowtopic=59270
help ons dan eiwitten vouwen, en help mee ziekten als kanker en zo te bestrijden in de vrije tijd van je chip...
http://sciencetalk.nl/forumshowtopic=59270
-
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Re: Botssnelheid
die hanze schreef op 12 May 2017 - 15:30:
Zoals jan al aangaf: wat is in hemelsnaam associatief denken??
Associatief denken is dat je er zaken bij haalt die met de kernvraag te maken heeft.
We gaan er (terecht) vanuit dat vervorming optreedt bij auto A en B tijdens botsing.
Kortom, wij associëren de vervorming aan het plotseling tot stilstand komen van de auto’s
Ondanks het feit dat de vervorming rekenkundig gekoppeld kan worden aan de snelheid van de auto’s, blijft het associatief denken.
De ruimte is in mijn optiek wel degelijk euclidisch (ga ik niet verder op in).
Ik blijf benieuwd naar een formule (die uitsluitend op snelheden is gebaseerd) dat antwoord geeft op de vraagstelling.
- die hanze
- Artikelen: 0
- Berichten: 897
- Lid geworden op: wo 19 aug 2009, 00:19
Re: Botssnelheid
Ok, in post #8 heb je associatief denken dan helemaal over boord gegooid  .
.
De vervorming is gerelateerd aan de kinetische energie die omgezet wordt in potentiele energie van de vervorming, net als het indrukken van een veer. Dit is de formule die je zoekt denk ik:
De vervorming is gerelateerd aan de kinetische energie die omgezet wordt in potentiele energie van de vervorming, net als het indrukken van een veer. Dit is de formule die je zoekt denk ik:
\(\frac{v^{2}m}{2}=kx\)
. De eerste term is de kinetische energie, met v snelheid auto (50 km/u) en m het gewicht. x is de mate van vervorming en k is een stijfheid van het materiaal. Dit laatste is zeer moeilijk theoretisch te bepalen aangezien hogere orde termen in rekening moeten genomen worden aangezien het waarchijnlijk om een complexe vervorming gaat. De analogie met een simpele veer is echter een goed model om het te begrijpen. Is je vraag nu beantwoord? -
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Re: Botssnelheid
Correctie 1: In post #8 heb ik associatief denken volledig geaccepteerd (is in bepaalde gevallen noodzakelijk).
Mijn vraag is hiermee niet beantwoord (het gaat mij nogmaals om de snelheid en niet de gevolgen ervan).
Terug naar post #8.
Uiterste stralingsgrens foton (gbi) is het uiterste van heelal.
Heelal dijt uit.
Heelal heeft (gbi) niét een midden.
Voor stralingsgolf (gbi) geldt: Heeft niét een midden.
Voor stralingsgolf (gbu) geldt: Heeft wél een midden.
Daarom zou het best eens kunnen dat vragen van bovenstaand kaliber uitsluitend van buitenaf gezien bekeken moeten te worden.
Uitwerking.
Foton als golf is bolvormig.
Voor uiterste stralingsgrens foton (gbi) als uiterste van heelal geldt: Er is sprake van verplaatsing foton.
Voor uiterste stralingsgrens foton (gbu) als uiterste van heelal geldt: Er is sprake van groter worden bol.
Voor uiterste stralingsgrens object zonder massa (gbi) als uiterste van heelal geldt: Snelheid van beweging (verplaatsing) is enkel (1) * c.
Voor uiterste stralingsgrens object zonder massa (gbu) als uiterste van heelal geldt: Snelheid van beweging (groter worden) is dubbel (2) * c.
Vereenvoudigd weergegeven.
Voor object zonder massa (gbu) geldt: Snelheid van beweging (groter worden) is afhankelijk van snelheid tegenpool.
Voor object zonder massa (gbi) geldt: Snelheid van beweging (verplaatsing) is onafhankelijk van snelheid tegenpool.
Voor object met massa (gbu) geldt: Snelheid van beweging (kleiner worden) is onafhankelijk van snelheid tegenpool.
Voor object met massa (gbi) geldt: Snelheid van beweging (verplaatsing) is afhankelijk van snelheid tegenpool.
Ik kan amper tot tien tellen, daarom kan ik het niet controleren.
Kortom, ik geef het op.
Correctie 2: Wij leven inderdaad in een niét euclidische ruimte.
In post #8 sprak ik van een uiterste stralingsgrens foton (is een bol) als uiterste van heelal.
In ieder geval heb ik een bijdrage kunnen leveren waarom de formule in post #8 problemen geeft.
Jan en jij: Bedankt voor je reactie!
Mijn vraag is hiermee niet beantwoord (het gaat mij nogmaals om de snelheid en niet de gevolgen ervan).
Terug naar post #8.
Uiterste stralingsgrens foton (gbi) is het uiterste van heelal.
Heelal dijt uit.
Heelal heeft (gbi) niét een midden.
Voor stralingsgolf (gbi) geldt: Heeft niét een midden.
Voor stralingsgolf (gbu) geldt: Heeft wél een midden.
Daarom zou het best eens kunnen dat vragen van bovenstaand kaliber uitsluitend van buitenaf gezien bekeken moeten te worden.
Uitwerking.
Foton als golf is bolvormig.
Voor uiterste stralingsgrens foton (gbi) als uiterste van heelal geldt: Er is sprake van verplaatsing foton.
Voor uiterste stralingsgrens foton (gbu) als uiterste van heelal geldt: Er is sprake van groter worden bol.
Voor uiterste stralingsgrens object zonder massa (gbi) als uiterste van heelal geldt: Snelheid van beweging (verplaatsing) is enkel (1) * c.
Voor uiterste stralingsgrens object zonder massa (gbu) als uiterste van heelal geldt: Snelheid van beweging (groter worden) is dubbel (2) * c.
Vereenvoudigd weergegeven.
Voor object zonder massa (gbu) geldt: Snelheid van beweging (groter worden) is afhankelijk van snelheid tegenpool.
Voor object zonder massa (gbi) geldt: Snelheid van beweging (verplaatsing) is onafhankelijk van snelheid tegenpool.
Voor object met massa (gbu) geldt: Snelheid van beweging (kleiner worden) is onafhankelijk van snelheid tegenpool.
Voor object met massa (gbi) geldt: Snelheid van beweging (verplaatsing) is afhankelijk van snelheid tegenpool.
Ik kan amper tot tien tellen, daarom kan ik het niet controleren.
Kortom, ik geef het op.
Correctie 2: Wij leven inderdaad in een niét euclidische ruimte.
In post #8 sprak ik van een uiterste stralingsgrens foton (is een bol) als uiterste van heelal.
In ieder geval heb ik een bijdrage kunnen leveren waarom de formule in post #8 problemen geeft.
Jan en jij: Bedankt voor je reactie!
-
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Re: Botssnelheid
Heb alsnog een poging gewaagd met onderstaand resultaat.
Uitwerking post #13 vervalt hierbij.
Uitwerking (correctie).
Foton als golf is bolvormig.
Als waar is:
Als waar is:
Vereenvoudigd weergegeven.
Voor snelheid van beweging (groei) van heelal geldt: Is 2c.
Voor snelheid van beweging (verplaatsing) van foton geldt: Is 1c.
Voor optellen van snelheden geldt:
a is foton a.
b is foton b.
Vab is snelheid-verplaatsing foton a t.o.v. b.
Vg is snelheid-groei heelal (= 2c).
Va is snelheid-verplaatsing foton a (= 1c).
Vb is snelheid-verplaatsing foton b (= 1c).
Voor Va geldt: Andere snelheid (< c) doet geen recht aan snelheid Vg (wordt < 2c).
Als waar is:
Bijvoorbeeld:
Als waar is:
Uitwerking post #13 vervalt hierbij.
Uitwerking (correctie).
Foton als golf is bolvormig.
Als waar is:
- Voor uiterste stralingsgrens foton (gbi) als uiterste van heelal geldt: Er is sprake van verplaatsing foton.
- Voor uiterste stralingsgrens foton (gbu) als uiterste van heelal geldt: Er is sprake van groter worden bol.
Als waar is:
- Voor uiterste stralingsgrens (gbi) als uiterste van heelal geldt: Snelheid van beweging (verplaatsing) is enkel (1) * c.
- Voor uiterste stralingsgrens (gbu) als uiterste van heelal geldt: Snelheid van beweging (groter worden) is dubbel (2) * c.
Vereenvoudigd weergegeven.
Voor snelheid van beweging (groei) van heelal geldt: Is 2c.
Voor snelheid van beweging (verplaatsing) van foton geldt: Is 1c.
Voor optellen van snelheden geldt:
- Vab = (Vg + Vb) / (1 + (Vg * Vb) / Va^2.
a is foton a.
b is foton b.
Vab is snelheid-verplaatsing foton a t.o.v. b.
Vg is snelheid-groei heelal (= 2c).
Va is snelheid-verplaatsing foton a (= 1c).
Vb is snelheid-verplaatsing foton b (= 1c).
Voor Va geldt: Andere snelheid (< c) doet geen recht aan snelheid Vg (wordt < 2c).
Als waar is:
- Voor rekenresultaten voor heelal (gbi) geldt: Komt overeen met formule in post #8.
- Voor heelal (gbi) geldt: Er is een relativiteit die verder gaat dan die van Einstein.
Bijvoorbeeld:
- Voor heelal (gbi) geldt: Is begrensd.
- Voor heelal (gbu) geldt: Is onbegrensd (is paradoxaal).
- Voor heelal (gbi) geldt: Ruimte is niét euclidisch.
- Voor heelal (gbu) geldt: Ruimte is wél euclidisch.
Als waar is:
- Voor toekomst heelal geldt: Uiterste stralingsgrens dijt (bij bereiken van grootte ≈ 1E+35 m) even snel uit als het krimpt.
- Voor heelal geldt: Heeft op termijn één grootte.
- Voor heelal geldt: Er is niét sprake van inkrimpen uiterste stralingsgrens heelal.
-
Kampen540
- Artikelen: 0
- Berichten: 84
- Lid geworden op: di 09 mei 2017, 14:26
Re: Botssnelheid
NABRANDER
Terug naar de vraagstelling post #1.
In post #8 heb ik gesteld:
De formule van post #8 (aangepast voor krimp) geldt dan ook voor de vraagstelling van post #1/
Als waar is:
Als waar is:
Als waar is:
Als waar is:
Als waar is:
Terug naar de vraagstelling post #1.
In post #8 heb ik gesteld:
- Je kan de auto conform foton ook als stralingsgolf voorstellen die krimpt naar nul met 50 km/u.
Ook deze stralingsgolf (gbi) heeft niét een midden (is onjuist: heeft wél een midden).
De formule van post #8 (aangepast voor krimp) geldt dan ook voor de vraagstelling van post #1/
Als waar is:
- Voor uiterste stralingsgolf auto (gbi) geldt: Heeft wél een midden.
- Voor uiterste stralingsgolf foton (gbi) geldt: Heeft niét een midden.
Als waar is:
- Voor uiterste stralingsgolf auto geldt: Er is zowel sprake van groei en krimp.
- Heelal (uiterste stralingsgolf foton) dijt uit.
- Voor uiterste stralingsgolf foton geldt: Er is uitsluitend sprake van groei.
Als waar is:
- Voor uiterste stralingsgolf (gezien vanuit midden) auto geldt: Er is wél een horizon voorbij de stralingsgolf.
- Voor uiterste stralingsgolf (gezien vanuit midden) foton geldt: Er is niét een horizon voorbij de stralingsgolf.
Als waar is:
- Voor snelheid uiterste stralingsgolf auto geldt: Er is niet constant (bestuurder kan gas geven).
- Voor snelheid uiterste stralingsgolf foton geldt: Er is wél constant.
Als waar is:
- Voor snelheid uiterste stralingsgolf auto geldt: Is door bestuurder gedefinieerd (bestuurder bepaalt de snelheid).
- Voor snelheid uiterste stralingsgolf foton geldt: Er is wél constant.
- Voor snelheid uiterste stralingsgolf foton geldt: Is door ??? gedefinieerd (in ieder geval niet door mij).
- Voor snelheid hemellichamen geldt: Heeft snelheid = c minus opgenomen bewegingsenergie tijdens vorming.