Ik heb een vraag over halfgeleiders.
Als ik het goed begrijp is het verschil tussen de geleidende band en de valentie band qua energie klein genoeg om hem door verhitting of andere processen de electronen genoeg energie te geven om naar de geleidende band over te springen vanuit de valentie band?
Nu is mijn vraag? Hoe doet warmte (bij verhitting) dit?
Ik dacht dat warmte de kinetische energie van de atomen en moleculen aan gaf en niet die van de energie van electronen. Of heeft warmte ok gewoon energie aan een electron?
En nog een vraag.
Waarom zit het Fermi niveau van een halfgeleider precies in het midden van deze banden waar ze voor het energie niveau even ver van de geleidingsband af zitten als van de valentie band.
Halfgeleider
Moderator: physicalattraction
- Antoon
- Artikelen: 0
- Berichten: 1.750
- Lid geworden op: di 01 mar 2005, 22:09
- Elmo
- Artikelen: 0
- Berichten: 3.437
- Lid geworden op: ma 27 okt 2003, 13:47
Re: Halfgeleider
Ja, door verhitting gebeurt dit een heel klein beetje. Het effect is sterk (exponentieel) temperatuursafhankelijk, maar in normaal gebruik is het nog steeds zeer klein. Bijvoorbeeld: Si heeft een bandgap van ~1 eV en bij kamertemperatuur (300 K == 25 meV) kun je met Fermi-Dirac statistiek uitrekenen dat de electronconcentratie in de geleidingsband zeer laag is (huiswerk: hoe laag?).
Hier staat een mooie uitleg over het Fermi niveau. Conceptueel is het zo het makkelijkste voor te stellen: Het Fermi-niveau is het hoogste energieniveau van het materiaal dat met elektronen gevuld zou kunnen zijn (bij het absolute nulpunt). Als het niveau in de bandgap ligt, dan zijn daar geen electrontoestanden en dus wordt het niet echt gevuld. Het niveau geeft dus eigenlijk aan hoeveel energie een gemiddeld electron in het systeem heeft.
Typische situatie voor een halfgeleider:
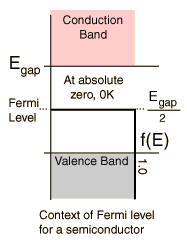
Als het Fermi-niveau in de geleidingsband terecht is gekomen, dan noemen we het materiaal een metaal (want dan is de geleiding zeer goed).
Algemeen verhaal over halfgeleiders. Typisch voor halfgeleiderfysica, vind ik, is dat als je het echt goed wil begrijpen je toch de boeken in zult moeten. De meeste teksten op het internet zijn niet echt geweldig (m.u.v. Britney's Guide to Semiconductor Physics).
En ja, de thermische energie geeft zeker ook meer kinetische energie aan de electronen.
Hier staat een mooie uitleg over het Fermi niveau. Conceptueel is het zo het makkelijkste voor te stellen: Het Fermi-niveau is het hoogste energieniveau van het materiaal dat met elektronen gevuld zou kunnen zijn (bij het absolute nulpunt). Als het niveau in de bandgap ligt, dan zijn daar geen electrontoestanden en dus wordt het niet echt gevuld. Het niveau geeft dus eigenlijk aan hoeveel energie een gemiddeld electron in het systeem heeft.
Typische situatie voor een halfgeleider:

Als het Fermi-niveau in de geleidingsband terecht is gekomen, dan noemen we het materiaal een metaal (want dan is de geleiding zeer goed).
Algemeen verhaal over halfgeleiders. Typisch voor halfgeleiderfysica, vind ik, is dat als je het echt goed wil begrijpen je toch de boeken in zult moeten. De meeste teksten op het internet zijn niet echt geweldig (m.u.v. Britney's Guide to Semiconductor Physics).
En ja, de thermische energie geeft zeker ook meer kinetische energie aan de electronen.
Never underestimate the predictability of stupidity...
- Antoon
- Artikelen: 0
- Berichten: 1.750
- Lid geworden op: di 01 mar 2005, 22:09
Re: Halfgeleider
ah, het valt nu wel op zijn plaats. dankje
Geeft die F(E) hier de kans aan van een electronen in die gap als ze gecondenseerd zijn?
of heb ik het nu helemaal verkeerd begrepen?
deze F(E) functie is toch de bose-einstein distrubutie?
Geeft die F(E) hier de kans aan van een electronen in die gap als ze gecondenseerd zijn?
of heb ik het nu helemaal verkeerd begrepen?
deze F(E) functie is toch de bose-einstein distrubutie?
-
Anonymous
- Artikelen: 0
Re: Halfgeleider
de f(E) staat volgens mij voor de Fermi-Dirac verdeling. f(E) = 1/(exp[(E-Ef)/kBT]-1). Als T = 0k, dan zijn de hoogste bezette niveaus deze met de Fermi- energie Ef (vandaar ook het fermi boloppervlak), als T>0k, dan springen elektronen naar hogere energieniveaus, en de dichtheid van de elektronen per energieinterval wordt dan gekarakteriseerd volgens de f(E) verdeling. ik heb een mooi figuurtje hoe deze f(E) functie inwerkt op het energie niveau (enkel in de zone XBT), maar ik weet niet hoe je hier figuurtje inplaatst, dus zelf wa proberen te interpreteren.
-
Anonymous
- Artikelen: 0
Re: Halfgeleider
mmm, ik bedoelde met de zone waarin de wet inwerkt: zone kBT, blijkbaar iets misgelopen met de code ...? ofwel omdat ik iets fout deed (is waarschijnlijker  ). bedoelde dus de zone "constante van boltzmann x T, die uiteraard van een kleine grootteorde is vergeleken met Ef.
). bedoelde dus de zone "constante van boltzmann x T, die uiteraard van een kleine grootteorde is vergeleken met Ef.