- Professor Puntje
- Artikelen: 0
- Berichten: 7.570
- Lid geworden op: vr 23 okt 2015, 23:02
Re: Kromtestraal van de ruimtetijd (2)
Ik heb gisteren nogmaals op internet en in mijn eigen boekenverzameling gezocht naar een simpele uitleg van de lichtbuiging volgens de ART maar heb zo'n uitleg niet gevonden. Aan alle populaire en/of semi-klassieke verklaringen die wel voorgeven het simpel te houden ontbreken essentiële onderdelen, of ze komen net als mijn eerdere eigen verklaring op de verkeerde waarde uit. Het staat voor mij nu als een paal boven water dat het gewoonweg niet simpel kan. Je ontkomt (als je het precies wilt begrijpen) uiteindelijk niet aan zwaar pakket wiskunde.
-
DParlevliet
- Artikelen: 0
- Berichten: 369
- Lid geworden op: wo 02 okt 2013, 10:47
Re: Kromtestraal van de ruimtetijd (2)
Nu een stap verder. Uit mijn eenvoudige benadering volgt voor de ruimtekromming Rk = c2/2g (#165). Nu geldt ook dat g = GM1/Rm2
Stel nu dat de ruimtekrommingstraal Rk gelijk is aan de afstand tot een centrale massa Rm. Dan draait een foton voortdurend rondom de massa en ontsnapt niet meer. Uit gelijkstellen volgt R = 2G.M1/c2, en dat is inderdaad de formule voor de Schwarzschildstraal van een zwart gat. Blijkbaar is dat ook eenvoudig af te leiden (bij massa's ben ik er nog niet uit).

En als het op internet stond zou ik het hier niet gepost hebben. Dat is geen sterk wetenschappelijk tegenargument. Waarschijnlijk gebruikt iedereen daar de ART-formules. Mijn afleidingen zijn eenvoudig, dus fouten daarin moeten simpel zijn te weerleggen.
Stel nu dat de ruimtekrommingstraal Rk gelijk is aan de afstand tot een centrale massa Rm. Dan draait een foton voortdurend rondom de massa en ontsnapt niet meer. Uit gelijkstellen volgt R = 2G.M1/c2, en dat is inderdaad de formule voor de Schwarzschildstraal van een zwart gat. Blijkbaar is dat ook eenvoudig af te leiden (bij massa's ben ik er nog niet uit).
En als het op internet stond zou ik het hier niet gepost hebben. Dat is geen sterk wetenschappelijk tegenargument. Waarschijnlijk gebruikt iedereen daar de ART-formules. Mijn afleidingen zijn eenvoudig, dus fouten daarin moeten simpel zijn te weerleggen.
- Michel Uphoff
- Moderator
- Artikelen: 0
- Berichten: 8.167
- Lid geworden op: di 01 jun 2010, 00:17
Re: Kromtestraal van de ruimtetijd (2)
Uit gelijkstellen volgt R = 2G.M1/c2, en dat is inderdaad de formule voor de Schwarzschildstraal van een zwart gat.
De straal waarbij een foton in een min of meer stabiele cirkelvormige omloopbaan rond een black hole gedwongen wordt is die van de photonsphere, en die is 3/2 van de Schwarzschildradius:
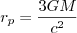 .
.In geval van een theoretisch black hole met de massa van de Zon dus ongeveer 4500 meter. Ieder object (of foton) dat dichter bij dan deze straal komt, wordt naar binnen gedwongen en spiraliseert onvermijdelijk naar de waarnemingshorizon. Deze 3/2rs omloopbaan voor fotonen geldt overigens alleen bij een gesimplificeerd niet roterend zwart gat, bij roterende (Kerr) black holes wordt het nog een tik gecompliceerder.
-
DParlevliet
- Artikelen: 0
- Berichten: 369
- Lid geworden op: wo 02 okt 2013, 10:47
Re: Kromtestraal van de ruimtetijd (2)
Ik heb me ook afgevraagd hoe die factor van precies 1,5 verklaard kan worden, maar ik heb dat nooit ergens gevonden. Misschien een apart effect dat met stabiliteit te maken heeft. Mijn afleiding is eenvoudig, dus alleen gebaseerd op de ruimtekromming ongeacht het effect van fotonen daarop.
- HansH
- Artikelen: 0
- Berichten: 4.664
- Lid geworden op: wo 27 jan 2010, 14:11
Re: Kromtestraal van de ruimtetijd (2)
Er wordt steeds gesproken over een straal Rp, maar tov welk referentiekader geldt die straal? is dat tov de stilstaande waarnemer op afstand? en zo ja hoe wordt het effect dat de lengte ook relatief is daarbij betrokken? zou dat een verklaring kunnen zijn?DParlevliet schreef: Ik heb me ook afgevraagd hoe die factor van precies 1,5 verklaard kan worden, maar ik heb dat nooit ergens gevonden. Misschien een apart effect dat met stabiliteit te maken heeft. Mijn afleiding is eenvoudig, dus alleen gebaseerd op de ruimtekromming ongeacht het effect van fotonen daarop.
De verdere berekeningen van dparlevliet zijn denk ik allemaal gebaseerd op het vallende lift principe en daarvan had ik al eerder via mathcad laten zien dat je dan niet op de factor 2 komt die je dan nog aan kromming van de ruimte te kort komt. dus ook voor de Schwarzschildradius als je die op die manier probeert te bepalen.
-
DParlevliet
- Artikelen: 0
- Berichten: 369
- Lid geworden op: wo 02 okt 2013, 10:47
Re: Kromtestraal van de ruimtetijd (2)
Ik neem aan ten opzichte van een waarnemer die niet met hoge snelheid beweegt t.o.v. het zwarte gat (of andersom).
In mijn redenering komt geen vallende lift voor en de eenvoudige formules leveren de factor 2 en de Schwarzschildradius.
In mijn redenering komt geen vallende lift voor en de eenvoudige formules leveren de factor 2 en de Schwarzschildradius.
- Professor Puntje
- Artikelen: 0
- Berichten: 7.570
- Lid geworden op: vr 23 okt 2015, 23:02
Re: Kromtestraal van de ruimtetijd (2)
Voor newtoniaanse ideeën over zwarte gaten zie:
https://en.wikipedia.org/wiki/Dark_star_(Newtonian_mechanics)
https://en.wikipedia.org/wiki/Dark_star_(Newtonian_mechanics)
- HansH
- Artikelen: 0
- Berichten: 4.664
- Lid geworden op: wo 27 jan 2010, 14:11
Re: Kromtestraal van de ruimtetijd (2)
in die link staat ook onderstaande verklaring voor de factor 2, alleen begrijp ik de zin niet helemaal. Er zijn blijkbaar 2 bijdragen en de newton theorie beschrijft er maar 1. Dus wat is dan de 2e bijdrage?Professor Puntje schreef: Voor newtoniaanse ideeën over zwarte gaten zie:
https://en.wikipedia.org/wiki/Dark_star_(Newtonian_mechanics)
Light-bending effects
If Newtonian physics does have a gravitational deflection of light (Newton, Cavendish, Soldner), general relativity predicts twice as much deflection in a lightbeam skimming the Sun. This difference can be explained by the additional contribution of the curvature of space under modern theory: while Newtonian gravitation is analogous to the space-time components of general relativity's Riemann curvature tensor, the curvature tensor only contains purely spatial components, and both forms of curvature contribute to the total deflection.
-
flappelap
- Artikelen: 0
- Berichten: 1.356
- Lid geworden op: za 30 dec 2017, 10:49
Re: Kromtestraal van de ruimtetijd (2)
Zonder de expliciete berekening erbij te hebben gepakt, lees ik dit als volgt: In de Newtonse benadering van de alg.rel.theorie blijven alleen de Riemann-tensor componenten \(R^{i}_{\ 0j0}\) over (waarvan het spoor de Laplaciaan van de Newton-potentiaal oplevert), terwijl in de volledig relativistische berekening \(R^{i}_{\ jkm}\) ook bijdraagt.in die link staat ook onderstaande verklaring voor de factor 2, alleen begrijp ik de zin niet helemaal. Er zijn blijkbaar 2 bijdragen en de newton theorie beschrijft er maar 1. Dus wat is dan de 2e bijdrage?
Light-bending effects If Newtonian physics does have a gravitational deflection of light (Newton, Cavendish, Soldner), general relativity predicts twice as much deflection in a lightbeam skimming the Sun. This difference can be explained by the additional contribution of the curvature of space under modern theory: while Newtonian gravitation is analogous to the space-time components of general relativity's Riemann curvature tensor, the curvature tensor only contains purely spatial components, and both forms of curvature contribute to the total deflection.
-
DParlevliet
- Artikelen: 0
- Berichten: 369
- Lid geworden op: wo 02 okt 2013, 10:47
Re: Kromtestraal van de ruimtetijd (2)
Zie #165, daar staan beide bijdragen.
- HansH
- Artikelen: 0
- Berichten: 4.664
- Lid geworden op: wo 27 jan 2010, 14:11
Re: Kromtestraal van de ruimtetijd (2)
ik zie daar een horizontale snelheid ct en vertikale versnelling 1/2gt^2 en dat was wat de lift in vrije val doet volgens het equivalentieprincipe, maar hoe je dan tot een verklaring voor nog een factor 1/2gt^2 komt zie ik nietDParlevliet schreef: Zie #165, daar staan beide bijdragen.
-
flappelap
- Artikelen: 0
- Berichten: 1.356
- Lid geworden op: za 30 dec 2017, 10:49
Re: Kromtestraal van de ruimtetijd (2)
Ik ben benieuwd of dat maximum-beginsel nog verder onderbouwd kan worden. Het maakt in elk geval al geen deel uit dan de postulaten van de SRT, maar mogelijk is het binnen de SRT wel af te leiden?
Het idee dat deeltjes waar geen krachten op werken geodeten volgen is de relativistische variant van Newtons 2e wet, oftewel een bewegingsvergelijking. De postulaten van de SRT zeggen alleen iets over de symmetrieen die inertiaalwaarnemers verbinden.
-
DParlevliet
- Artikelen: 0
- Berichten: 369
- Lid geworden op: wo 02 okt 2013, 10:47
Re: Kromtestraal van de ruimtetijd (2)
In A zie de baan die een massa volgt. De vraag is nu hoe hard de ruimte aan die massa 'trekt' om hem die baan te laten volgen. Hoe sterk is de ruimtekromming aan de massa gekoppeld. Daar kwam ik niet uit, dus ik keek naar de praktijk: stel je kijkt vanuit de massa, bijvoorbeeld door in B de massa vast te leggen. Dan weten we dat er een kracht F = m.a = m.g op die massa werkt, veroorzaakt door de kromming van ruimte, eigenlijk van het nul-niveau. De massa wil daar naar toe vallen, waar het in rust is, waar er geen krachten meer op werken. Bevries nu eens de eindsituatie van de grafiek, waarbij de massa naar het nulvieau valt en daar tot rust komt en denk andersom: wat voor weg moet hij daarvoor volgens newton afleggen: dat is ook s = 0,5.a.t2 dus 0,5.g.t2.HansH schreef: ik zie daar een horizontale snelheid ct en vertikale versnelling 1/2gt^2 en dat was wat de lift in vrije val doet volgens het equivalentieprincipe, maar hoe je dan tot een verklaring voor nog een factor 1/2gt^2 komt zie ik niet
Ik moet iedere keer weer piekeren bij deze redenering, dus misschien zit er ergens een fout in, maar die kon ik niet vinden.
- HansH
- Artikelen: 0
- Berichten: 4.664
- Lid geworden op: wo 27 jan 2010, 14:11
Re: Kromtestraal van de ruimtetijd (2)
Nog eens terug kijkend naar mijn eerdere input #135 lijkt me dat mogelijk toch bij nader inzien de verklaring voor de extra kromming. Immers de ART gaat ervan uit dat de natuurwetten gelijk moeten blijven ongeacht de situatie waar de waarnemer zich in bevind.
Nu leidde het idee van de serie vallende liften ertoe dat hierdoor een kromming van de ruimte ontstaat omdat men geen onderscheid kan maken tussen een lichtstraal die door een in vrije val zijnde lift gaat onder invloed van een zwaartekrachtsveld en een stilstaande lift in hetzelfde zwaartekrachtsveld. Dus moet het licht wel de afbuiging volgen overeenkomstig de serie vallende liften. Dat verklaart echter maar de helft van de kromming.
De serie vallende liften roteren echter niet, ervan uitgaande dat ze alleen versneld worden in de richting van het zwaartekrachtsveld. Dus het licht wat door de laatste lift gaat heeft een andere hoek tov die lift vergeleken met de eerste lift. dus vanuit de lichtstraal gezien gaat die gewoon rechtdoor en ziet een serie liften op zich afkomen die langzaam roteren. Maar volgens het equivalentieprincipe zou een lichtstraal zonder zwaartekrachtsveld ook gewoon rechtdoor gaan door dezelfde serie vallende liften, maar dan zou die lichtstraal dezelfde serie liftten tegenkomen, echter zonder rotatie omdat er zonder zwaartekrachtsveld immers helemaal geen afbuiging is.
Op basis van die 2 situaties zou men toch onderscheid kunnen maken tussen de situatie van de lichtstraal die door de serie vallende liften gaat in een zwaartekrachtsveld en zonder zwaartekrachtsveld omdat in het ene geval wel rotatie zou plaatsvinden en in het andere geval niet.
Omdat volgens de ART men geen onderscheid kan maken tussen een in vrije val zijnde baan onder invloed van een zwaartekrachtsveld en een in vrije val zijnde baan zonder zwaartekrachtveld moet het wel zo zijn dat de ruimte ook nog een krommingscomponent heeft die net dat verschil wegwerkt. Omdat de oorzaak van de extra rotatie nu juist de afbuiging was moet de ruimte nog een extra identieke kromming maken om ervoor te zorgen dat er geen onderscheid meer is tussen beide situaties, dus dat zou dan verklaren waarom de kromming 2x zo groot is.
Nu leidde het idee van de serie vallende liften ertoe dat hierdoor een kromming van de ruimte ontstaat omdat men geen onderscheid kan maken tussen een lichtstraal die door een in vrije val zijnde lift gaat onder invloed van een zwaartekrachtsveld en een stilstaande lift in hetzelfde zwaartekrachtsveld. Dus moet het licht wel de afbuiging volgen overeenkomstig de serie vallende liften. Dat verklaart echter maar de helft van de kromming.
De serie vallende liften roteren echter niet, ervan uitgaande dat ze alleen versneld worden in de richting van het zwaartekrachtsveld. Dus het licht wat door de laatste lift gaat heeft een andere hoek tov die lift vergeleken met de eerste lift. dus vanuit de lichtstraal gezien gaat die gewoon rechtdoor en ziet een serie liften op zich afkomen die langzaam roteren. Maar volgens het equivalentieprincipe zou een lichtstraal zonder zwaartekrachtsveld ook gewoon rechtdoor gaan door dezelfde serie vallende liften, maar dan zou die lichtstraal dezelfde serie liftten tegenkomen, echter zonder rotatie omdat er zonder zwaartekrachtsveld immers helemaal geen afbuiging is.
Op basis van die 2 situaties zou men toch onderscheid kunnen maken tussen de situatie van de lichtstraal die door de serie vallende liften gaat in een zwaartekrachtsveld en zonder zwaartekrachtsveld omdat in het ene geval wel rotatie zou plaatsvinden en in het andere geval niet.
Omdat volgens de ART men geen onderscheid kan maken tussen een in vrije val zijnde baan onder invloed van een zwaartekrachtsveld en een in vrije val zijnde baan zonder zwaartekrachtveld moet het wel zo zijn dat de ruimte ook nog een krommingscomponent heeft die net dat verschil wegwerkt. Omdat de oorzaak van de extra rotatie nu juist de afbuiging was moet de ruimte nog een extra identieke kromming maken om ervoor te zorgen dat er geen onderscheid meer is tussen beide situaties, dus dat zou dan verklaren waarom de kromming 2x zo groot is.
-
DParlevliet
- Artikelen: 0
- Berichten: 369
- Lid geworden op: wo 02 okt 2013, 10:47
Re: Kromtestraal van de ruimtetijd (2)
Inderdaad, dat is een meer principiële verklaring.
Ik heb de discussie over de lift niet gevolgd omdat ik vooral op zoek ben naar de meest simpele fysiek begrijpbare verklaring die voor mensen met MBO-wiskunde te volgen is (gaat maar tot een bepaalde grens natuurlijk). De principiële verklaring is weer net iets te abstract, maar ook wel mooier natuurlijk. Het klopt beter bij het verhaal dat Einstein opeens inzag dat een dubbele buiging nodig was, en niet na veel gereken (als dat verhaal klopt).
Ik heb de discussie over de lift niet gevolgd omdat ik vooral op zoek ben naar de meest simpele fysiek begrijpbare verklaring die voor mensen met MBO-wiskunde te volgen is (gaat maar tot een bepaalde grens natuurlijk). De principiële verklaring is weer net iets te abstract, maar ook wel mooier natuurlijk. Het klopt beter bij het verhaal dat Einstein opeens inzag dat een dubbele buiging nodig was, en niet na veel gereken (als dat verhaal klopt).