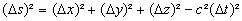peterdevis schreef:Door dat de metriek waarmee we een afstand meten een negatieve factor bezit (namelijk deze van de tijdscoördinaat, niet te verwarren met de eigentijd) is het zo dat des te krommer het oppervlak des te korter het afgelegde interval in de ruimtetijd
deze zin snap ik niet. ik zal mijn bedenkselen even neer zetten dat helpt misschien met het beanwoorden van mijn vraag.
Het interval (als ik je minicursus goed begrijp) is:
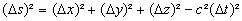
Maar ik snap niet hoe ik uit deze formule kan afleiden dat hoe krommer de ruimte tijd is, des te kleiner is het interval.
Ik zou denken. Ik weet ook niet wat rijmte-tijd kromming eigenlijk inhoudt
dat het interval dus kleiner word doordat de negatieve factor. (die van de tijd) groter wordt, en daarom moet de tijd dus eigenlijk langer duren, aangezien je eerst zei (na de verbetering van de gast) dat hoe kleiner het interval hoe langzamer de tijd verstrijkt.
er zijn mij dus 2 dingen ontgaan.
1:Waarom is het interval kleiner als de ruimtetijd krommer is?
2:Als de tijd groter word dan zou je met de formule voor het interval denken dat het interval kleiner word (want je moet c²t² eraf halen) hoe zit dit dan?[/url]
Dat wordt ook erg lastig om hiermee je vraag op te lossen: je gebruikt namelijk de Minkowskimetriek, en die gebruik je louter in de speciale rel.theorie. Je gequote interval kan dus alleen worden gebruikt in situaties zonder massa. In de algemene heb je andere metrieken. Die metriek verkrijg je door de veldvergelijkingen van Einstein op te lossen.
Stel, je hebt een grote bol in de ruimte hangen. Stel dat die bol zoiets als een ster is. Die ster bevat energie, en impuls. Je kunt dan iets voor die ster opstellen, wat fysici de "energie-momentum tensor" noemen ( in het engels ook wel stress-energy tensor ") Die tensor is een object ( in dit geval als een matrix te schrijven ) met alle informatie over de energie en de impuls van het object. Einstein zijn veldvergelijkingen zeggen dan: deze tensor is gelijk aan een constante maal de Einsteintensor. Dan moet je nog ff weten wat die Einsteintensor is.
Die Einsteintensor beschrijft de kromming van de ruimte-tijd. Nou heb je in de wiskunde de Riemanntensor die krommingen beschrijft, dus waarom niet stellen dat de energie-momentum tensor gelijk is aan een constante maal de Riemanntensor? Omdat je een natuurkundig idee hebt als energiebehoud. Hier komt de natuurkunde te pas! Die stelt dat de afgeleide ( aangepast voor een gekromd oppervlak ) van de energie-momentum tensor 0 moet zijn: energie en impuls zijn behouden. Dus moet de afgeleide van de tensor die de kromming van de ruimte-tijd beschrijft ook 0 zijn. Want wat je aan de ene kant van het = teken hebt, geldt ook voor de andere kant van het = teken. De afgeleide van de Riemanntensor is zeker niet 0, maar je kunt met behulp van deze Riemanntensor een object maken wat wel 0 oplevert als je haar afleidt: dat is dus die Einsteintensor. Dus, je krijgt dat
Energie-momentum tensor = constante maal Einstein tensor.
Wat een verhaal, maar nu komt de clou: De Einstein tensor wordt uitgedruk in de Riemanntensor, en deze wordt weer uitgedrukt in de metriek. Bij een gegeven energie en momentum van een object kun je dus de metriek bepalen, en dus ook hoe de ruimte tijd ( want dat is het oppervlak waar we het de hele tijd over hebben ) wordt gekromd.
En die metriek beschrijft het ruimte-tijd interval, wat jij ds noemt. Bij een massa zal deze metriek massa-termen bevatten, en je kunt aantonen dat hierdoor de tijd van een waarnemer in een zwaartekrachtsveld langer duurt dan voor een waarnemer die zich in een vlakke metriek bevindt, dus ver buiten dat zwaartekrachtsveld. En dus ver vanaf die bol. Een bekende oplossing is de Schwarzschild oplossing. Ik hoop dat het zo wat duidelijker is, ook al heet ik geen Peter
Dat heeft natuurlijk alles te maken met de afstand willen definieren mbv de Euclidische metriek, terwijl je hier werkt met een metriek die niet louter positieve termen bevat. 