Tripelpunt

[jkien]

Ik twijfel over de term tripelpunt, omdat ik het begrip nooit gebruik. Klopt het dat het tripelpunt voor een blokje ijs in de buitenlucht, bij een relatieve luchtvochtigheid van bijna 100%, gelijk is aan het vriespunt, 0°C? (En onder het vriespunt in onverzadigde lucht gaat het ijs sublimeren.)

[Xilvo]

Het tripelpunt is het punt waar vaste fase, vloeibare fase en gasfase met elkaar in evenwicht zijn (Wikipedia).

Bij water is dat bij 0,01 °C.
In de buitenlucht heb je niet alleen de dampdruk van waterdamp maar ook van de lucht. Het vriespunt zal dan dalen, ik denk tot precies die 0,00 °C. Maar dat is geen tripelpunt meer.

[OOOVincentOOO]

Wellicht nog vermelden dat voor water in het triple punt de druk en temperatuur een rol spelen: 0.01 [°C], 0.61 [kPa[] [Wiki]. Het triple punt is immers in het p-T diagram. Naar mijn veronderstelling immer de totale druk onderhevig op vloeistof-vaste stof.

Erg verhelderend en mooi experiment:
https://youtu.be/Juz9pVVsmQQ

[jkien]

In de buitenlucht heb je niet alleen de dampdruk van waterdamp maar ook van de lucht. Het vriespunt zal dan dalen, ik denk tot precies die 0,00 °C. Maar dat is geen tripelpunt meer.

De "druk", die is weergegeven op de verticale as van de grafiek, is volgens mij uitsluitend de partiele druk van de waterdamp. Waarom zou de partiele druk van de overige lucht ook een rol spelen?


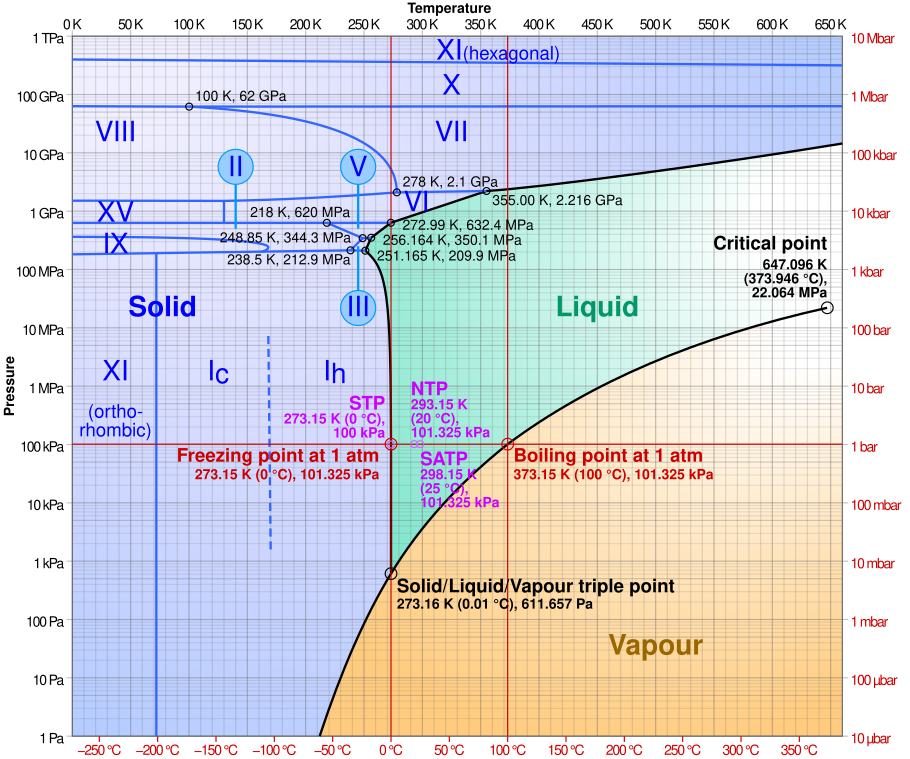
(Bron van afbeelding: wikipedia)

[Marko]

Partiële druk en zo lijkt me allemaal niet zo van toepassing. Als er naast water ook lucht aanwezig is, kan er per definitie geen tripelpunt zijn. Het tripelpunt is een punt omdat druk en temperatuur vastliggen. Dat (afwezigheid van vrijheidsgraden) kan voor 3 fasen alleen als je maar 1 component hebt.

[jkien]

Wikipedia stelt "Even if the total pressure of a system is well above the triple point of water, provided that the partial pressure of the water vapor is 611.657 pascals, then the system can still be brought to the triple point of water. " Dat betekent toch dat het in de grafiek uitsluitend om de partiele druk van de waterdamp gaat, en dat de overige lucht er niet toe doet?

[OOOVincentOOO]

Voor mij is het ook enige jaren geleden, inderdaad het is de dampdruk.

Maar de vloeistof is ook onderhevig aan een druk dit is grotendeels de luchtdruk. Dit is toch het kookpunt? Om in het tripel punt te komen dient de vloeistof toch in/nabij het kookpunt te zijn? De totale druk dient dan gelijk/nabij dampdruk te zijn? [Wiki]

https://chem.libretexts.org/Bookshelves ... e_Diagrams

Hier nog gevonden op Physics exchange.
https://physics.stackexchange.com/quest ... m-of-water

[Xilvo]

Waarom zou de partiele druk van de overige lucht ook een rol spelen?

Omdat water in volume toeneemt als het bevriest is het energetisch gunstiger als dat vriespunt lager wordt bij toenemende druk.
De gemiddelde onderlinge afstand tussen de moleculen moet toenemen bij bevriezen maar dat werk je tegen door druk aan te leggen.

Wikipedia:

Regelation is the phenomenon of ice melting under pressure and refreezing when the pressure is reduced.
//
Regelation was discovered by Michael Faraday. It occurs only for substances such as ice, that have the property of expanding upon freezing, for the melting points of those substances decrease with the increasing external pressure. The melting point of ice falls by 0.0072 °C for each additional atm of pressure applied. For example, a pressure of 500 atmospheres is needed for ice to melt at −4 °C.[2]

[Xilvo]

De "druk", die is weergegeven op de verticale as van de grafiek, is volgens mij uitsluitend de partiele druk van de waterdamp. Waarom zou de partiele druk van de overige lucht ook een rol spelen?


(Bron van afbeelding: wikipedia)

De druk langs de verticale as kan niet de partiele druk van waterdamp zijn, bijvoorbeeld bij 0 °C kan de partiele druk nooit 100 kPa zijn.

In de grafiek is ook te zien dat de temperatuur bij het tripelpunt 273,16 K is, en bij het vriespunt bij 100 kPa 273,15 K.

[jkien]

Ok. Ik was in verwarring geraakt door de sublimatielijn in het fasediagram van water, wat ik interpreteerde alsof er buiten die lijn geen sublimatie is. Maar die coëxistentielijn markeert blijkbaar alleen de toestanden waar evenwicht bestaat tussen sublimatie en rijping (depositie), terwijl sublimatie zonder evenwicht overal in het "solid phase" gebied optreedt. Een blokje ijs buiten in de winterse vrieskou, evenals wasgoed dat in de vrieskou te drogen hangt, bevindt zich op de rode lijn.

1

[Marko]

Wikipedia stelt "Even if the total pressure of a system is well above the triple point of water, provided that the partial pressure of the water vapor is 611.657 pascals, then the system can still be brought to the triple point of water. " Dat betekent toch dat het in de grafiek uitsluitend om de partiele druk van de waterdamp gaat, en dat de overige lucht er niet toe doet?

Ik was allemaal wat te kort door de bocht. Als je meer fasen hebt, heb je meer vrijheidsgraden. Die beschrijven de samenstelling van het systeem. Als je de samenstelling van je systeem vastlegt zal een coëxistentie van 3 fasen nog steeds bij één unieke combinatie van druk en temperatuur plaatsvinden. Dus ook bij mengsels kan/zal er sprake zijn van een tripelpunt. Alleen bepaalt de samenstelling waar die combinatie precies ligt. Dat gezegd hebbende, in veel gevallen zullen druk en temperatuur nauwelijks afwijken van de samenstelling, en de druk is in dit verband de partieeldruk.

Even een simpel voorbeeld: een smeltend ijsblokje in een gesloten vat met waterdamp, op het tripelpunt. Op dat moment zijn de 3 fasen in evenwicht. Gezien waterdamp hier in evenwicht is met vloeibaar water kun je concluderen dat de omgevingsdruk gelijk is aan de dampspanning van water. Nu laten we stikstofgas in het vat lopen. De omgevingsdruk neemt toe. Er moet zich een nieuw evenwicht instellen, maar in hoeverre verschilt dat van de situatie direct na het binnenlaten van de stikstof?

In grote lijnen: niks. Stikstof lost nauwelijks op in water en ook niet in ijs. In evenwicht bevat de vaste fase nauwelijks stikstof, en de vloeibare fase ook niet. In beide fasen is de molfractie van het water dus nagenoeg 1 en dus is de dampspanning van het water gelijk aan de dampspanning van zuiver water, dus gelijk aan wat die al was voor het inbrengen van de stikfstof. Deze dampspanning is de bijdrage van de waterdamp aan de totaaldruk, met andere woorden de partieeldruk van het water.

De gasfase is dus weliswaar van samenstelling veranderd en de totaaldruk is toegenomen door het toevoegen van de stikfstof. Maar er is verder geen condensatie of rijping opgetreden en de temperatuur is dus gelijk aan wat die was. Het tripelpunt bevindt zich dus bij een zodanige druk dat de partieeldruk van water in de gasfase gelijk is aan de totale druk in het tripelpunt als er enkel water zou zijn, en de temperatuur is gelijk aan die in het tripelpunt.

Deze vlieger gaat uiteraard alleen op voor (zeer) beperkt oplosbare gassen c.q. mengbare vloeistoffen. Bij (deels) mengbare stoffen zal de samenstelling veel sterker van invloed zijn op de ligging van het tripelpunt / de tripelpunten.

[OOOVincentOOO]

Even een simpel voorbeeld: een smeltend ijsblokje in een gesloten vat met waterdamp, op het tripelpunt. ... Nu laten we stikstofgas in het vat lopen. De omgevingsdruk neemt toe. Er moet zich een nieuw evenwicht instellen, maar in hoeverre verschilt dat van de situatie direct na het binnenlaten van de stikstof?

Volgens mijn begrip:
Door het inbrengen van stikstof veranderend het kookpunt/verdamping van de vloeistof. De stikstof druk veranderd het kookpunt en de rate verdampend water uit de vloeistof.

Met mijn begrip dient men de vaste/vloeistof niet te vergeten de verdamping hier is afhankelijk van de totale omgevingsdruk. Dus volgens mij kan men het tripelpunt alleen experimenteel/praktisch bereiken in een "vacuum" met slechts waterdamp(druk).

Stel door de omgevingsdruk (N2/O2) zal een waterdruppeltje/smeltend ijs zich op een ander punt bevinden in het p-T diagram.

Waar maak ik mijn denkfout? Alle reacties wat ik lees stemmen niet overeen met mijn inzicht. Kan iemand mij verlossen waar ik fout ben?

Erg verhelderend en mooi experiment:
(als je goed oplet zie je ook het effect van de oppervlakte spanning meespelen)
https://youtu.be/Juz9pVVsmQQ

[OOOVincentOOO]

Zie ook vergelijkbare vraag:
https://physics.stackexchange.com/quest ... m-of-water

In the phase diagram of water, in relation to the gas phase region and bordering lines, what is the relevant pressure?

The pressure we are talking about is the pressure on (and inside) the water. Imagine pure water in a can; squeeze the can and you increase the pressure. This is the pressure we are talking about.

Is it the partial vapour pressure of water, or is it the total pressure including contributions from other gases?

Neither nor. If other liquids/gases/substances are present (if you have a mixture), then you basically have another material. Then this phase diagram doesn't apply. Another material has another phase diagram.

Begin een beetje te twijfelen aan alles wat ik geleerd heb! Hier staat het beschreven zoals ik het begrijp en ooit geleerd heb.

[jkien]

iedereen bedankt voor de uitleg!

[Marko]

Volgens mijn begrip:
Door het inbrengen van stikstof veranderend het kookpunt/verdamping van de vloeistof. De stikstof druk veranderd het kookpunt en de rate verdampend water uit de vloeistof.

Dat klopt niet. Verdamping hangt samen met de dampspanning van een stof, en gaat door totdat de partieeldruk gelijk is aan de dampspanning. Als je een vloeistof hebt bestaande uit enkel stof X en een gasfase bestaande uit enkel Y, dan kan de druk nog zo hoog zijn, er zal altijd wat X verdampen en mengen met de moleculen Y. De totale druk neemt dan toe.

Dit klinkt onlogisch, dat zelfs als de druk heel hoog is, deze nog kan toenemen maar het is wellicht toch als volgt in te zien. De druk an sich is namelijk helemaal niet van belang. De druk, als in kracht per oppervlakte, heeft zelf geen invloed op de vraag of een molecuul wel of niet genegen is om de vloeistof te verlaten. De reden dat druk invloed heeft, is omdat die samenhangt met de concentratie aan moleculen in de gasfase.

Bij een zuivere stof geldt: Een hogere druk betekent meer deeltjes per volume-eenheid, dus meer deeltjes die per tijdseenheid langs een gegeven oppervlak vliegen en dus meer kans dat deze deeltjes de oplossing in wippen. En een hogere druk vertaalt zich dus in een andere verhouding tussen ontsnappen uit de vloeistof en (terug) de vloeistof in gaan, en netto verdampt daardoor minder van de vloeistof. Of: verschuift de verhouding tussen de hoeveelheid moleculen in de vloeistof en in de gasfase. Maar uiteindelijk is het dus niet de druk, maar de concentratie aan deeltjes, die van invloed is op de verdamping. En daarom moet je niet naar de totaaldruk, maar naar de partieeldruk kijken.