Wat is spin?
Moderator: physicalattraction
-
Ja, die ene gek zo.
- Artikelen: 0
- Berichten: 28
- Lid geworden op: di 21 mar 2006, 19:29
Wat is spin?
Ik ben me (eindelijk) gaan verdiepen in quantumfysica..waarbij ik op het principe 'spin' stuitte, hetgeen wordt bepaald door 'magnetic moment' en 'angular momentum' - Wat wordt hiermee bedoeld?
- Antoon
- Artikelen: 0
- Berichten: 1.750
- Lid geworden op: di 01 mar 2005, 22:09
Re: Wat is spin?
kun je je vraag specificeren? wat snap je er niet van?
Spin is een eigenschap van een deeltjes, wat bij geladen deeltjes zorgt voor een magnetischmoment. maar spin bepaald ook of een deeltje een fermion of een boson is.
Spin is een eigenschap van een deeltjes, wat bij geladen deeltjes zorgt voor een magnetischmoment. maar spin bepaald ook of een deeltje een fermion of een boson is.
-
Ja, die ene gek zo.
- Artikelen: 0
- Berichten: 28
- Lid geworden op: di 21 mar 2006, 19:29
Re: Wat is spin?
nou, mijn vraag is eigenlijk; Wat is magnetisch moment, en wat is 'angular momentum'? (geen idee hoe ik het zou moeten vertalen)
- Antoon
- Artikelen: 0
- Berichten: 1.750
- Lid geworden op: di 01 mar 2005, 22:09
Re: Wat is spin?
Magnetisch moment is het moment van een magnetisch veld.
Het angularmomentum ,is het baanimpulsmoment van een electron.
Het impuls van een deeltje is:
p=mv
het baanimpuls(deeltje in cirkel beweging) van een deeltje is:
L=mvr
r is hier de straal.
Bij electronen om een kern heb je ook temaken met een baanimpuls. uit de Bohrtheorie (het voorstellen van een electron als een bewegendelanding om een geladen kern) volgende :
L=
Ën bij het oplossen van de Schrödinger vergelijking voor het waterstofatoom kregen we ook een baanimpuls met als oplossing
L²=l(l+1) ²
²
(wie kan dit herleiden?)
Omdat een electron een bewegende lading heeft maakt het een magnetisch veld. En omdat het in een cirkel gaat, ook nog eens een magnetischmoment die voldoet aan de vergelijking:
magnetischmoment = stroom * oppervlakte
hier een plaatje voor de duidelijkheid
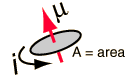
dus
µ=IA
die I(Stroom)en de A(oppervlakte) kun je omschrijven zodat je de volgende vergelijking krijgt:
Het angularmomentum ,is het baanimpulsmoment van een electron.
Het impuls van een deeltje is:
p=mv
het baanimpuls(deeltje in cirkel beweging) van een deeltje is:
L=mvr
r is hier de straal.
Bij electronen om een kern heb je ook temaken met een baanimpuls. uit de Bohrtheorie (het voorstellen van een electron als een bewegendelanding om een geladen kern) volgende :
L=
\(\frac{nh}{2\pi}\)
(dat kan ik voor je herleiden als je wilt)Ën bij het oplossen van de Schrödinger vergelijking voor het waterstofatoom kregen we ook een baanimpuls met als oplossing
L²=l(l+1)
(wie kan dit herleiden?)
Omdat een electron een bewegende lading heeft maakt het een magnetisch veld. En omdat het in een cirkel gaat, ook nog eens een magnetischmoment die voldoet aan de vergelijking:
magnetischmoment = stroom * oppervlakte
hier een plaatje voor de duidelijkheid
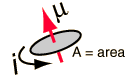
dus
µ=IA
die I(Stroom)en de A(oppervlakte) kun je omschrijven zodat je de volgende vergelijking krijgt:
\(µ=\frac{-e \cdot L}{2m_e}\)
-
Ja, die ene gek zo.
- Artikelen: 0
- Berichten: 28
- Lid geworden op: di 21 mar 2006, 19:29
Re: Wat is spin?
Ik begin er al iets van te snappen - maar je uitleg roept nog alleen maar meer vragen op (dat gebeurt vrijwel altijd als mensen iets tegen me zeggen)
Mijn kennis van dit onderwerp is zeer beperkt, vandaar dat ik mij afvraag wat 'n' inhoudt in L=
en ongeveer even belangrijk; Hoe komt men aan deze formules?
(dat wordt waarschijnlijk een lang verhaal, dus als je het versimpeld zou kunnen uitleggen zou ik daar geen probleem mee hebben )
)
En deze stroom van een elektron - is deze altijd hetzelfde of kan deze verschillen?
Mijn kennis van dit onderwerp is zeer beperkt, vandaar dat ik mij afvraag wat 'n' inhoudt in L=
\(\frac{nh}{2\pi}\)
en de 'l' in L²=l(l+1)² en ongeveer even belangrijk; Hoe komt men aan deze formules?
(dat wordt waarschijnlijk een lang verhaal, dus als je het versimpeld zou kunnen uitleggen zou ik daar geen probleem mee hebben
En deze stroom van een elektron - is deze altijd hetzelfde of kan deze verschillen?
- Antoon
- Artikelen: 0
- Berichten: 1.750
- Lid geworden op: di 01 mar 2005, 22:09
Re: Wat is spin?
n is de baan in welke het electron zin. (hoofdkwantumgetal) en l is het baanquantum getal . dit zijn twee andere dingen, maar het hoofdquantumgetal (n) bepaald de waarden die het baanquantumgetal mag aannemen.
Hoe maken ze deze formule's
de formule
L=nh/2pi.gif = n kun je krijgen door Borhmodel te volgen. Met wat electrodynamica en de aanname dat electronen golven zijn en zo de juiste straal moeten hebben moet het lukken.
kun je krijgen door Borhmodel te volgen. Met wat electrodynamica en de aanname dat electronen golven zijn en zo de juiste straal moeten hebben moet het lukken.
maar de andere formule voor L. kun je krijgen door de schrödinger vergelijking voor een electron in een waterstof atoom optelossen, dit is erg lastig, en dat kan ik dan ook niet.
De met de stroom van een electron word gewoon de stroom bedoeld die een electon ook veroorzaakt in een stroomdraadje. Het is volgens mij wel mogelijk dat sommiga electronen een hogere stroom hebben dan andere.
Hoe maken ze deze formule's
de formule
L=nh/2pi.gif = n
maar de andere formule voor L. kun je krijgen door de schrödinger vergelijking voor een electron in een waterstof atoom optelossen, dit is erg lastig, en dat kan ik dan ook niet.
De met de stroom van een electron word gewoon de stroom bedoeld die een electon ook veroorzaakt in een stroomdraadje. Het is volgens mij wel mogelijk dat sommiga electronen een hogere stroom hebben dan andere.
-
Ja, die ene gek zo.
- Artikelen: 0
- Berichten: 28
- Lid geworden op: di 21 mar 2006, 19:29
Re: Wat is spin?
oké bedankt 
*snapt er alweer iets meer van.
*snapt er alweer iets meer van.
-
Spuit11
- Artikelen: 0
- Berichten: 217
- Lid geworden op: zo 17 apr 2005, 12:49
Re: Wat is spin?
Schrödinger gaat er van uit dat er spraake is van orbitalen waarin een waarschijnlijkheidsfactor ligt waarbinnen men een elektron kan aantreffen. L2 hier in geeft het orbitaal aan waarbinnen het elektron zich bevind.Om het orbitaal weer te geven neem je de golffunctie in het kwadraat.Antoon schreef:Magnetisch moment is het moment van een magnetisch veld.
Het angularmomentum ,is het baanimpulsmoment van een electron.
Het impuls van een deeltje is:
p=mv
het baanimpuls(deeltje in cirkel beweging) van een deeltje is:
L=mvr
r is hier de straal.
Bij electronen om een kern heb je ook temaken met een baanimpuls. uit de Bohrtheorie (het voorstellen van een electron als een bewegendelanding om een geladen kern) volgende :
L=\(\frac{nh}{2\pi}\)(dat kan ik voor je herleiden als je wilt)
Ën bij het oplossen van de Schrödinger vergelijking voor het waterstofatoom kregen we ook een baanimpuls met als oplossing
L²=l(l+1)²
(wie kan dit herleiden?)
Omdat een electron een bewegende lading heeft maakt het een magnetisch veld. En omdat het in een cirkel gaat, ook nog eens een magnetischmoment die voldoet aan de vergelijking:
magnetischmoment = stroom * oppervlakte
hier een plaatje voor de duidelijkheid
dus
µ=IA
die I(Stroom)en de A(oppervlakte) kun je omschrijven zodat je de volgende vergelijking krijgt:
\(µ=\frac{-e \cdot L}{2m_e}\)