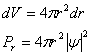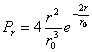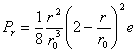Les 1 : De vroege quantumtheorie
De quantumtheorie rond 1900
Quantummechanica beschrijft het gedrag van zeer kleine deeltjes, deeltjes die zo klein zijn dat de gewone Newtonse natuurkunde niet meer op gaat. De quantummechanica is daarom een aanvulling op de Newtoniaanse natuurkunde. De eerste aanwijzingen van deze quantummechanica kwamen rond de 1900. Planck kwam er achter dat energie niet bestaat uit een continu spectrum maar uit een gekwantiseerd (discreet) spectrum. Planck beweerde dat de energie die elektronen bezitten in een stralend voorwerp gekwantiseerd zijn volgens:
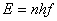
Waarin:
E = energie elektron
h = constante van Planck
f = frequentie uitgezonden foton van stralend voorwerp
n = een geheel getal (n = 1,2,3,..).
Deze quantumhypothese van Planck zegt dat de energie E geen continu waarde kan hebben. Dit komt door de waarde n, die alleen gehele getallen aan kan nemen. Hij kwam op deze conclusie nadat er verschillende inconsistenties waren geconstateerd bij de beschrijving van de frequentiespectrum van het uitzenden van licht bij een gloeiend object (verschuivingwet van Wien).
In 1905 legde Einstein de link naar fotonen. Hij concludeerde dat als energie moest bestaan uit discrete hoeveelheden, fotonen dat ook moesten zijn. Deze ontdekking leidde tot het foto-elektrische effect. Door dit effect kan een elektrische stoom worden opgewekt met een fotocel. De fotonen kunnen elektronen vrijmaken die vervolgens in een elektrische kring kunnen worden gemeten. Een andere theorie van Einstein voorspelde dat een elektron weg kan worden geschoten uit een stuk metaal. Het foton zal dan in zijn geheel worden geabsorbeerd door het desbetreffende elektron en deze zal een bepaalde snelheid meekrijgen. De energie die het foton bezit is dus ook de energie die een elektron meekrijgt is:
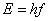
Waarin:
E = energie foton
h = constante van Planck
f = frequentie foton.
Dit lijkt heel erg op de eerste formule. Deze formule legt een directe link tussen de frequentie van een foton en de energie die hij bezit. In 1923 kwam deed A.H. Compton experimenten met elektronen die werden gebombardeerd met fotonen die niet in hun geheel werden geabsorbeerd, maar gedeeltelijk hun energie afstaan. Het elektron en het foton veranderen dan van richting en impuls. Voor het elektron resulteerde dat in een snelheidsverandering en voor het foton resulteerde dat in een golflengteverandering. Doordat het foton energie verliest is aan de formule te zien dat zijn frequentie kleiner wordt.
Een ander voorbeeld van de interactie tussen fotonen en materie is paarvorming. Uit een foton kan een elektron en een positron ontstaan. Dit is te verklaren volgens de bekende formule E=mc^2 waarin m de massa´s voorstellen van het elektron en het positron, en c de lichtsnelheid. Als bij de m de massa wordt ingevuld van een elektron, na uitwerking van de formule zal men uitkomen op een energie van 1.02 MeV. Dit is dus de minimale energie die een foton moet bezitten om d.m.v. paarvorming een elektron en een positron te kunnen maken. Het interessante van paarvorming is dat uit een deeltje pure energie (foton), massa kan ontstaan. Door nu het elektron en het positron bij elkaar te laten komen zullen ze desintegreren en er zal daarbij een foton ontstaan. Bij het ontstaan van een elektron, positron paarvorming is het logisch dat de wet van behoud van energie en de wet van behoud van lading behouden blijft.
Het golfkarakter van materie
In 1923 kwam Louis de Broglie tot de conclusie dat alle materie rechtstreeks met golfkaraktereigenschappen in verband kon worden gebracht. Dit wordt ook wel De-Broglie-golflengte genoemd:
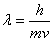
Waarin:
Labda = golflengte van deeltje
h = constante van Planck
m = massa van deeltje
v = snelheid van deeltje.
Voor huis tuin en keuken objecten komt er een zeer kleine golflengte uit (10
-35). Golfkarakter eigenschappen van deze objecten zullen we dan ook niet zien. Pas als we zeer kleine objecten gaan bekijken zoals elektronen kunnen we hun golfkarakter in beeld brengen. Zoals bij het dubbele spleet experiment met elektronen, zie foto. Ook de elektronenmicroscoop werkt volgens het principe, doordat de golflengte van de gebruikte elektronen zeer klein is, is het oplossende vermogen van een elektronenmicroscoop zeer groot. Een optische microscoop is gelimiteerd doordat de golflengte van zichtbaar licht (300nm). Een transmissie elektronenmicroscoop haalt ongeveer 0.2 nm (een gedeelte wordt verloren door aberratie van de magnetische lenzen).
Bohr werkte in 1912 al een tijdje aan het atoommodel. Met behulp van dit model kon hij b.v. de straal van een waterstof atoom bepalen. Dit deed hij met behulp van de algemene formule van (baan) impulsmoment:
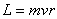
Waarin:
L = Baanimpulsmoment
m = massa elektron
v = snelheid elektron
r = straal van de baan van elektron.
Dit in samenwerking met de quantumvoorwaarde kwam hij op de volgende formule:
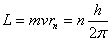
Waarbij n het quantumnummer voorstelt. Met behulp van de 2e wet van newton kan worden uitgerekend dat de kleinste straal (n1) van waterstof, 0.529x10
-10m groot is. Dit wordt ook wel de Bohr-straal genoemd. Omdat de afstand tot de atoomkern bekend is en ook de twee ladingen (atoomkern en elektron) kan er op eenvoudige wijze worden uitgerekend hoeveel energie er nodig is om het elektron in zijn geheel van het atoom te verwijderen:
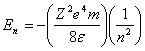
Waarin:
Z = atoomnummer van kern (voor waterstof is dit 1)
e = lading van elektron
m = massa elektron.
Voor de grondtoestand van waterstof (n = 1) komt men op -13.6 MeV (dit is een negatief getal omdat het energie kost om het elektron te verwijderen), een bedrag dat iedereen wel eens is tegengekomen. Zoals we zien zijn dus niet alleen de banen gequantiseerd maar ook de energieën van de elektronen die de banen beschrijven. Voor de 2e baan voor het elektron van het waterstof atoom ligt de waarde op -3.4 MeV. Om het elektron van baan 1 naar baan 2 te krijgen is dus 10,2 MeV nodig
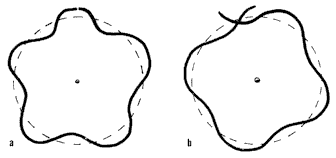
Bohr had hier geen stevig theoretische basis voor, maar de formules bleken wel experimenteel te kloppen. Het is dus meer een ruwe voorstelling van het atoom. Bohr kon namelijk niet verklaren waarom de banen gequantiseerd waren. Dus waarom die n er zo mooi in paste. In 1923 kwam De Broglie daar met een antwoord op: Een baan is pas stabiel als er een een geheel aantal golflengten in de omtrek passen. En dat kan pas volgens verschillende gehele waarden van pi.
 Het dubbele spleet experiment
Het dubbele spleet experiment
Dit is het experiment wat onmogelijk is te verklaren op iedere klassieke manier en welke meteen het hart raakt van de quantummechanica. Met dit experiment wordt bewezen dat elektronen net als golven met elkaar interfereren. Opvallend als men bedenkt dat er ook een interferentie patroon op treedt als er echter maar 1 elektron telkens in het kanon bevindt. Pas als een van de spleten wordt weggehaald zal het interferentie patroon verdwijnen. Een elektron kan dus met zichzelf interfereren. Het is dus niet alleen een deeltje maar bezit dus ook golfeigenschappen.
 De onbepaaldheidrelatie van Heisenberg
De onbepaaldheidrelatie van Heisenberg
De onbepaaldheidrelatie van Heisenberg vertelt iets over de onzekerheid waar je mee te maken krijgt als je een meting doet. Bij allerdaagse objecten zal je geen hinder van deze relatie ondervinden. Kijkt men nou naar hele kleine deeltjes dan gaat de onbepaaldheidrelatie zulk grote vormen aan nemen dat het een probleem oplevert in het vinden van de snelheid en de plaats van een deeltje. Of nog beter gezegd, het vinden van de exacte waarden van impuls (snelheid maal massa) en plaats:
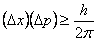
Waarin:
delta x = onzekerheid in de plaats
delta p = onzekerheid in de impuls
h = constante van Planck
Deze formule zegt dat als je de plaats met een grote zekerheid weet je niet een nauwkeurige uitspraak kan doen over de impuls.
Determinisme
In de jaren van de klassieke mechanica was het nogal duidelijk dat als je een biljartbal over een biljard tafel stoot, je precies kunt uitrekenen waar deze terechtkomt. Dit heeft tot gevolg dat als je dat met een biljartbal kan je het ook zou kunnen doen met een atoom. Als je dit denken voorzet kan je het ook met 2 atomen en ook met 100 atomen. Dus ook alle atomen in je hersenen. De volgende conclusie die je dan kan trekken is dat alles wat we doen is voorbestemd. En dat we dus ook geen eigen wil hebben. De mensen die zo denken worden deterministen genoemd.
De meeste antwoorden van quantummechanische problemen hebben een statistische karakter. Zoals het dubbele spleet experiment is het niet te voorspellen waar de elektronen komen, het is alleen mogelijk een kans op te geven waar de elektronen terecht kunnen komen. Natuurlijk is het zo dat hoewel alles wat er gebeurd willekeurig is, dit niks zegt over het feit dat de uitkomst al vastligt of niet. Hier eindigt de fysica en begint de filosofie, iets waar we in deze cursus niet verder op ingaan.
Schrodinger´s tijdonafhankelijke vergelijking in 1-dimensie
Dit is de uitgeklede versie van de schrodinger vergelijking. De echte komt in veel verschillende gedaantes voor en beschrijft deeltjes en drie dimensies met een tijd dimensie. In deze cursus beschrijven we de vergelijking met 1 ruimtedimensie en zonder tijddimensie. Dit geeft een goede inzicht aan wat er aan de grondslag ligt aan de beschrijving van de kleinste deeltjes in de natuurkunde.
Het is niet mogelijk de vergelijking van schrodinger te bewijzen uit nog fundamentelere natuurkunde, net zoals je de 2
e wet van Newton (F = m*a) ook niet is af te leiden uit nog fundamentelere formules. Daarom wordt hij hier niet bewezen maar meteen gegeven:
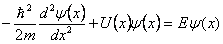
Waarin:
U = potentiële energie van deeltje (J)
E = totale energie van deeltje (J)
m = massa van het betreffende deeltje
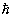
= constante van planck / 2π
Laat je niet afschrikken door zijn complexe uiterlijk, het valt reuze mee nu volgt een uitleg waarom. Als je deze vergelijking op zou lossen door bepaalde waarden voor U, E en m in zou vullen, zal je ψ als uitkomst krijgen, dit is de golffunctie die iets zegt over de kans (de werkelijke kans is
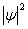
). Als we nou een vrij deeltje beschouwen, dan is de potentiële energie U = 0. We houden dan over:
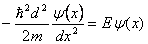
.
Zoals je kan zien is het niet meer dan een 2
e orde differentiaalvergelijking:
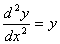
.
De uitkomst van zo´n vergelijking ziet er onder bepaalde omstandigheden uit als zoiets:
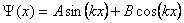
, dus eigenlijk niet meer dan een sinusfunctie eventueel met een cosinusfunctie daar bij opgeteld. De A en B zijn nader te bepalen constanten die worden verkregen uit randvoorwaarden die volgen uit waarden van het vraagstuk. Voor deze uitleg niet verder van belang.
Als we deze functie gaan tekenen dan zien we dat de functie zich onbegrensd laat tekenen van min-oneindig naar plus-oneindig. Dit lijkt misschien vreemd, maar omdat de kinetische energie precies bekend is (E, en dus ook de impuls), kan men geen uitspraak doen van de positie van het deeltje. Precies volgens het onzekerheidsprincipe.
Als we nu een geladen deeltje beschouwen die is opgesloten in een elektrische put, waarbij de randen zeer hoog zijn. Een elektrische put kan men voorstellen als een gewone put waar een bal in zit. Deze bal moet een bepaalde trap (energie) krijgen om er uit te komen. Een elektrische put is hetzelfde, alleen dan moet een geladen deeltje een bepaalde elektrische energie overwinnen om er uit te komen. Als nu de randen van deze potentiaalput oneindig hoog zijn zal het deeltje nooit kunnen ontsnappen. Een deeltje dat erin is gevangen zal dan een halve sinus beschrijven of een veelfout van de sinus. Dit komt ook voort als men randvoorwaarden gaat invullen van de differentiaalvergelijking: van de
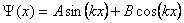
, zal B nul worden en de volgende formule ontstaan:
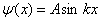
Waarin:
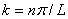
n = quantumgetal (1,2,3,...)
L = breedte potentiaalput.
In het volgende plaatje staan de eerste drie toestanden van het opgesloten elektron.
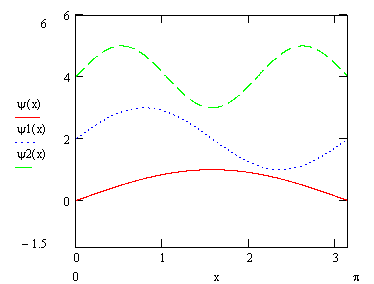
Bij n = 1 staat het deeltje in de grondtoestand, zijn energie is niet 0 maar heeft een bepaalde waarde. De volgende energietoestand is n = 2. Zoals al eerder is opgemerkt zijn energieën gekwantiseerd en dus niet continu. Als we deze energieën gaan uitrekenen komen we op:
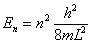
Zit een deeltje nou niet in een oneindig diepe potentiaalput, dan zal de Schrodingervergelijkin eruitzien als:
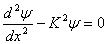
De algemene oplossing van deze differentiaalvergelijking is een functie met e-machten. De functie zal zoiets worden als:
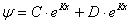
De twee e-machten laten zien dat de kans het deeltje buiten de potentiaalput tegen te komen nooit nul is. De e-macht functie zal niet toelaten de kans nul te laten worden.
Normalisatie voorwaarde
Omdat de uitkomst van een schrodervergelijking een kans is, is het wel de bedoeling dat de gehele kans om het deeltje tegen te komen 100% is. Voor het deeltje in de oneindig hoge put:
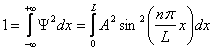
Waarin:
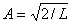
de 1 staat voor de 100% kans.
Samengevat
De Schrodingervergelijking is niet meer dan een 2e-orde differentiaalvergelijking. De oplossing van de differentiaalvergelijking geeft aan hoe groot de kans is het deeltje ergens aan te treffen.
1901 Planck Straling van een zwarte straler
1905 Einstein Foto-elektrisch effect
1913 Bohr kwantumtheorie van spectra
1922 Compton Verstrooiing van fotonen aan elektronen
1924 Pauli uitsluitingsprincipe
1925 de Broglie Materiegolven
1926 Schodinger Golfvergelijkingen
1927 Heisenberg Onzekerheidsprincipe
1927 Davisson en Germer Experiment van golfeigenschqappen van elektronen
1927 Born Interpretatie van de golffunctie
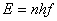
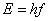
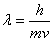
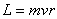
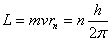
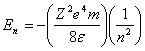


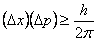
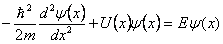
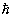 = constante van planck / 2π
= constante van planck / 2π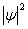 ). Als we nou een vrij deeltje beschouwen, dan is de potentiële energie U = 0. We houden dan over:
). Als we nou een vrij deeltje beschouwen, dan is de potentiële energie U = 0. We houden dan over: 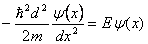 .
.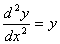 .
.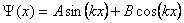 , dus eigenlijk niet meer dan een sinusfunctie eventueel met een cosinusfunctie daar bij opgeteld. De A en B zijn nader te bepalen constanten die worden verkregen uit randvoorwaarden die volgen uit waarden van het vraagstuk. Voor deze uitleg niet verder van belang.
, dus eigenlijk niet meer dan een sinusfunctie eventueel met een cosinusfunctie daar bij opgeteld. De A en B zijn nader te bepalen constanten die worden verkregen uit randvoorwaarden die volgen uit waarden van het vraagstuk. Voor deze uitleg niet verder van belang.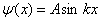
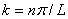
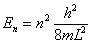
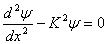
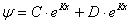
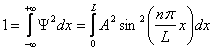
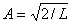
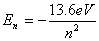
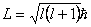
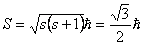
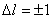

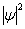 dV
dV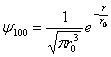
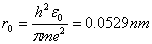 , ook wel de Bohr-straal genoemd.
, ook wel de Bohr-straal genoemd.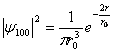
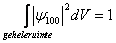
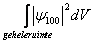 is de kans het elektron te vinden over een volume dV. Over de gehele ruimte is de kans natuurlijk 1. Het is in dit geval beter de waarschijnlijkheid aan te geven als functie van r en niet als functie van V. Men krijgt dan de radiale waarschijnlijkheidsdichtheid, Pr:
is de kans het elektron te vinden over een volume dV. Over de gehele ruimte is de kans natuurlijk 1. Het is in dit geval beter de waarschijnlijkheid aan te geven als functie van r en niet als functie van V. Men krijgt dan de radiale waarschijnlijkheidsdichtheid, Pr: