Voor de daadwerkelijke simulatie zelf ben ik bezig geweest om een aantal verschillende integratoren te implementeren, om te kijken welke van de mogelijke opties de meest geschikte is. Tot zover heb ik de volgende integratoren gebruikt:
- Euler
- Leapfrog (2e orde)*
- Runge-*** (4e orde)
- Yoshida (4e orde)*
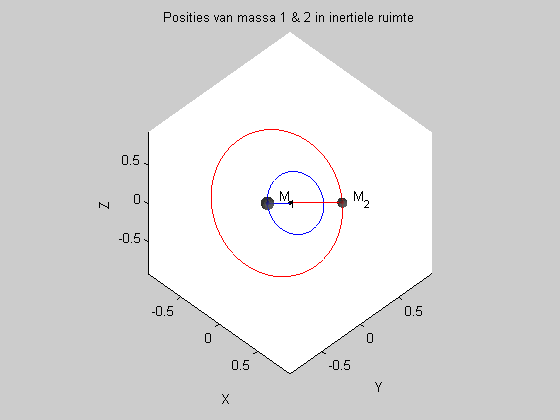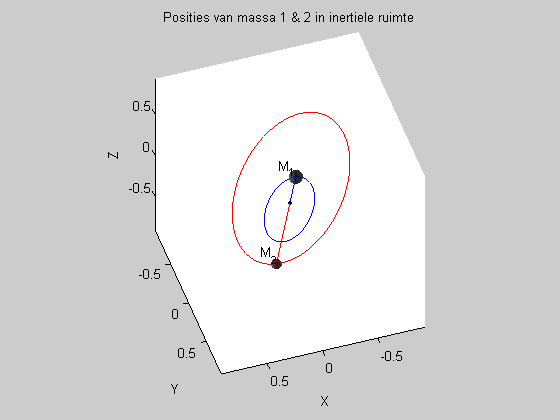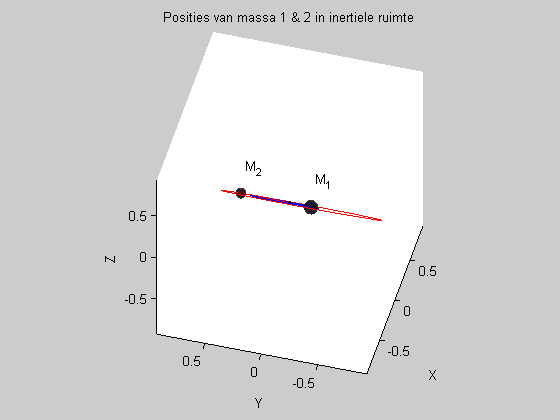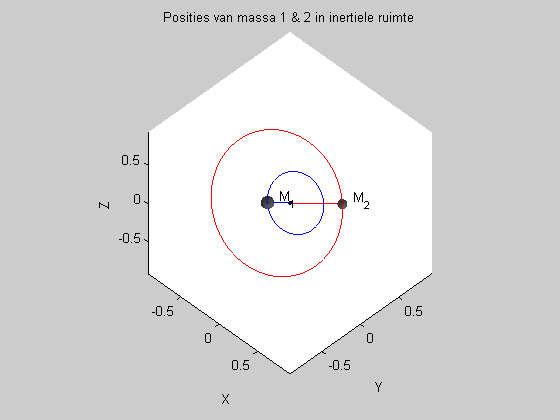
De twee integratoren die ik aangaf met een sterretje zijn symplectisch: reversibel en energiebehoudend, voor situaties als deze. Om de 'symplecticiteit' te testen houd ik voor iedere integratiestap de totale energie van het systeem bij (de som van de kinetische energie van alle massa's plus de som van alle relatieve potentialen), en kijk ik of die inderdaad praktisch constant blijft (of eigenlijk slechts kleine periodieke schommelingen vertoont, en geen drift).
Het rare is nu dat ik, na een serie testjes, merk dat bijvoorbeeld de leapfrog-integrator slechts eerste-orde gedrag vertoont (de fout in de totale energie is recht evenredig met de tijdstapgrootte), waar hij uiteraard tweede-orde gedrag (dus energiefout is evenredig met het kwadraat van de stapgrootte) zou moeten vertonen. Dit gedrag komt alleen maar voor wanneer ik een simulatie laat lopen waarin twee of meer lichamen vrij in een vlak bewegen. Wanneer ik de simulatie run zodanig dat er een van de twee massa's vastgehouden wordt (dus wanneer er slechts een enkele massa door de integrator 'onder handen genomen' wordt) vertoont de leapfrog-integrator gewoon het gewenste (en verwachte) gedrag.
Ik heb het vermoeden gekregen dat het te maken heeft met de manier waarop meerdere posities en versnellingen in een tijdstap berekend worden. Als toelichting zal ik in het kort beschrijven wat de leapfrog-integrator precies doet.
Stel de positievector van een massa 'i' in de simulatie op tijdstip 't' voor als \(x_i(t)\), de snelheidsvector als \(v_i(t)\), en de versnelling van dat object als \(a_i(t)\). De leapfrog-integrator doet om de volgende positie en snelheid te berekenen de volgende dingen:
\(x_i(t+1) = x_i(t) + v_i(t) \cdot \Delta t + a_i(t) \cdot \frac{\Delta t^2}{2}\)
dan\(a_i(t+1) = f(x_i(t+1))\)
(de functie 'f' stelt de berekening van de versnelling voor als functie van de positie) en vervolgens\(v_i(t+1) = v_i(t) + \frac{a_i(t) + a_i(t+1)}{2}\cdot \Delta t\)
Deze procedure werkt dus prima wanneer er slechts sprake is van een bewegend object en een vaste centrale aantrekker. Wanneer er echter meerdere bewegende objecten zijn ontstaat er een probleem. De volgende code voor twee objecten levert bijvoorbeeld niet het gewenste resultaat op:\(x_i(t+1) = x_i(t) + v_i(t) \cdot \Delta t + a_i(t) \cdot \frac{\Delta t^2}{2}\)
\(x_j(t+1) = x_j(t) + v_j(t) \cdot \Delta t + a_j(t) \cdot \frac{\Delta t^2}{2}\)
dan\(a_i(t+1) = f(x_i(t+1),x_j(t+1))\)
\(a_j(t+1) = f(x_i(t+1),x_j(t+1))\)
(beide versnellingen worden hier berekend gebruik makend van de nieuwe posities) en vervolgens\(v_i(t+1) = v_i(t) + \frac{a_i(t) + a_i(t+1)}{2}\cdot \Delta t\)
\(v_j(t+1) = v_j(t) + \frac{a_j(t) + a_j(t+1)}{2}\cdot \Delta t\)
Ook wanneer ik eerst alleen de positie en snelheid van massa 'i' integreer en daarna pas de positie en snelheid van massa 'j' integreer (gebruik makend van de situatie op tijdstip 't'), komt er niet het gewenste (tweede-orde) gedrag uit.Wie heeft er een idee van de correcte implementatie van dit algoritme wanneer het om meerdere objecten gaat?