Vallende stokken

[Kolio]

Hey,

Ik zit met een vraagje.

Stel je hebt 2 stokken, die aan 1 uiteinde met elkaar verbonden zijn. En ze kunnen vrij scharnieren.

Lengte: 2L. In het midden van elke stok bevindt zich een puntmassa m.

Stok 1 staat bijna recht omhoog langs de verticaal. Klein hoekje a t.o.v. verticaal

stok 2 staat daar weer op met klein hoekje b t.o.v. de verticaal alleen andere kant van verticaal.

het onderste uiteinde van stok 1 blijft op zijn plek.

De vraag is nu wat is de kinetische energie van het systeem??

Ik had zelf bedacht:

x massa stok1= L Sin a

y massa stok1= L Cos a

x massa stok2= 2L Sin a - L Sin b

y massa stok2= 2L Cos a + L Cos b

met

T=Tstok1+Tstok2= .5m ((dx massa stok1/dt)^2+(dy massa stok1/dt)^2))+.5m ((dx massa stok2/dt)^2+(dy massa stok2/dt)^2))

volgt bij mij dat

T= m L ( 2.5 L (da/dt)^2 +.5 db/dt L - 2 da/dt db/dt L Cos[a+b]

Ik twijfel eraan of dit goed is... Want als ik d.m.v. Lagrange-vergelijkignen dan d^2a/dt^2 en d^2b/dt^2 uitreken komt er iets heel vaags uit.

Alleen ik denk dat er een veel simpelere manier is om dit uit te rekenen.

Heeft iemand een idee?

Misschien met andere positievergelijkingen? of dat de snelheidsvergelijking anders moet?

Alvast bedankt

[dirkwb]

Kan je een tekening maken en is de lengte van elke stok L?

[Kolio]

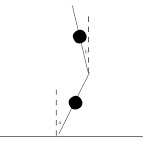
Hierbij een tekening.

Voor de duidelijkheid één stok heeft lengte 2L, dus de puntmassa bevindt zich op lengte L



Hoop dat het zo duidelijker is.

[eendavid]

In laagste orde moet je voor de kinetische energie

\(\frac{mL}{2}\left(5(\dot{a})^2-4\dot{a}\dot{b}+(\dot{b})^2\right)\)

bekomen. Dat lijkt overeen te stemmen met wat je schrijft (?). Merk op dat dit in 2de orde is in a en b. Heb je ook V tot 2de orde berekend?

[Kolio]

Wat betekend eerste orde en tweede orde?

gewoon de afgeleide naar t?

en ben je geen kwadraatje vergeten bij de L?

of staat \dot{a} voor iets anders dan \frac{da}{dt}?

Of snap ik ik het niet

edit:

Ik heb voor V:

V= mgL (3 Cos[a]+Cos) genomen

[eendavid]

OK, dat is allemaal nog in orde. Ik had al gebruik gemaakt van het feit dat a en b klein zijn (met orde bedoelde ik dus de graad van de taylorbenadering in a, b,

\(\dot{a}\)

,

\(\dot{b}\)

), maar dat is op dit punt nog niet per se nodig (hoewel iets eenvoudiger). Als je nu de Lagrangevergelijkingen neerschrijft zou je correcte vergelijkingen moeten krijgen (maar je zal ze niet kunnen integreren, daarvoor moet je gebruiken dat a en b klein zijn).

[Kolio]

Dus als ik het goed begrijp, en op Uw manier doe...

(ik krijg die latex-codes niet aan de praat, dus voeg ff een snel gemaakt plaatje toe met alles erin)

Volgt:



en met (1) en (2) kan ik dan eventueel de hoekversnellingen berekenen?

Klopt dit dan zo (voor hoek a en hoek b klein)?

[eendavid]

Opgelet! V tot tweede orde ontwikkelen! Anders benaderen we niet consistent, en komen we tot verkeerde resultaten.

edit: latex voer je hier in door

\( *code* [/tex ] te typen, maar dan zonder spatie.\)

[Kolio]

oke dus dan wordt

\( V=mgL(3-\frac{3}{2}\dot{a}^2+1-\frac{1}{2}\dot{b}^2)\)

en dan zou het moeten uitkomen?

[eendavid]

Als je

\(\dot{a}\)

vervangt door

\(a^2\)

, en idem voor b, is dat OK.

[ned118]

Kan iemand mij uitleggen hoe je die kleine hoek benadering precies doet?

[eendavid]

Je moet de Taylor expansie van de sinus en de cosinus functie gebruiken. Misschien bedoel je iets specifieker?

[ned118]

Ik heb sowieso geen sinus staan in mijn potentiele en kinetische energie, maar ik bedoel inderdaad iets specifieker.

voor mijn gevoel wordt T maar eerste orde benaderd en V wel tweede orde?

Alvast bedankt.

[ned118]

die kleine hoebenadering is wel gelukt.

Maar kan iemand mij uitleggen hoe ik uit de bewegingsvergelijkingen de hoeversnellingen kan halen?

[eendavid]

Je hebt twee gekoppelde tweede orde bronloze differentiaalvergelijkingen. Ken je een ansatz voor dergelijke vergelijking? Wat zou je als anzats nemen voor 1 zo'n differentiaalvergelijking?