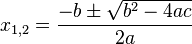IljaSmit schreef:Zoals het er staat, lijkt het simpel. Alleen het lukt mij niet om "t" uit te rekenen in deze formule
4,5 t^2 - 16,67 t -16,67+24,6 = 0
(mijn kennis is wat weggezakt in de loop der jaren)
Aangezien de kennis wat is weggezakt is het misschien handig te weten dat de bovenstaande vergelijking een vierkantsvergelijking is, en deze kan je altijd via de volgende methode oplossen:

Dit is de algemene vorm van een vierkantsvergelijking. Als we dit toepassen op jouw vergelijking is a=4,5. b=-16,67. c=-16,67+24,6 (m.a.w. c=7,93) en de x=t.
Nu ga je op zoek naar de discriminant, via de formule:

Hier heb je dan 3 mogelijkheden:
- D<0. Dit betekent dat je vergelijking geen enkele oplossing heeft. M.a.w. er is geen enkele waarde 't' waarvoor de vergelijking '0' zal worden.
D=0. Dit betekent dat je 1 oplossing hebt (die twee keer voorkomt, maar in praktijk moet zal jij daar geen rekening moeten mee houden denk ik.
D>0. Dit betekent dat je twee oplossingen zal vinden voor je vergelijking (maar in praktijk zal je in veel gevallen één van beiden kunnen elimineren omdat ze, realistisch gezien, niet kan).
Via de volgende formule kan je dan je uiteindelijke oplossingen bekomen:
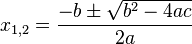
Merk op dat, als de discriminant gelijk is aan 0, beide oplossingen x1 en x2 gelijk worden aan elkaar, en dat dus de reden is dat je bij een discriminant gelijk aan 0 één oplossing hebt met multipliciteit 2.
Hopelijk ben je hier ook wat mee.