Nyquist zegt (voor zover mijn begrip strekt) dat de samplingfrequentie tweemaal de hoogste frequentie van het aangeboden spectrum moet zijn (en niet tweemaal de bandbreedte).
ook als antwoord op wat ZVDP schrijft:
Awel, dat is net wat ik wilde zeggen. Je begrip strekt dus lichtjes verkeerd. Nyquist moet 2x de breedte van je band zijn, wat bij laagdoorlaatsignalen inderdaad overeenkomt met 2x de hoogste frequentie. MAAR bij bandsignalen, zoals typisch uit een modulator komt, kun je dus veel efficiënter werken.
Strikt genomen moet je voor een optimaal resultaat dan wel pulsen sturen, en geen zero-order hold, maar dat maakt niet veel uit.
Je neemt dus de bandbreedt die je draaggolf inneemt. (de ruimte rond 133kHz, stel 10kHz). Dan heb je 2*de bandbreedte nodig daarvan , dus 20kHz. Je berekent dus hoe je sinus er zou moeten uitzien rond 133kHz, en je sampelt die functie aan een snelheid van 20kHz. Dit wil zeggen dat je iedere keer een paar perioden van je signaal overslaat, maar dat is helemaal niet erg.
Die samples komen dus uit je microprocessor (liefst puls, maar zero-order hold werkt volgens mij op het eerste zicht even goed) en stuur je nu door een bandfilter die de frequentie 128kHz-138kHz er uit filtert. Het resultaat is het signaal dat je zoekt.
Et voila, je hebt wat je moet hebben. Waarschijnlijk is de filter niet perfect enzo en moet je samplen aan 2.2*BW= 22kHz. Je maakt in feite gebruik van het aliasing-fenomeen, maar in plaats van de laagste frequenties te gebruiken zoals meestal het geval is, gebruik je de frequenties van de harmonische in de band die je wil hebben.
Moest het nog niet duidelijk zijn, vraag maar. In ieder geval lijkt dit me wat je zoekt, als je die samplerate omlaag wil halen.
Zie anders ook:
http://en.wikipedia.org/wiki/Sampling_theo...aseband_signals
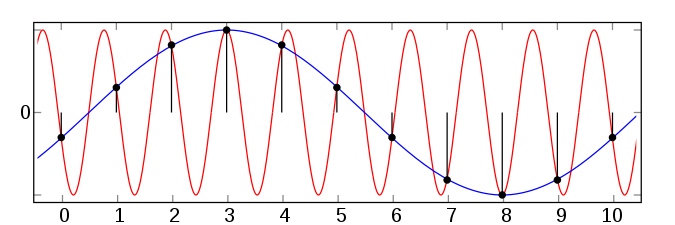
Noot: dit werkt enkel voor sinusgemoduleerde signalen, ik zie dat je ook andere signalen wilt maken, dat gaat daarmee niet (goed) werken.

 voor
voor 