Evenwichten vs. ontbinden in krachten

[Alopex]

Hoewel een onderdeel van de vraag veel op een vraag/oefening lijkt (en het er ook een is) ga ik het toch wagen ze hier op te zetten aangezien de oefening al opgelost is maar er een tegenstrijdigheid bestaat tussen twee methodes.

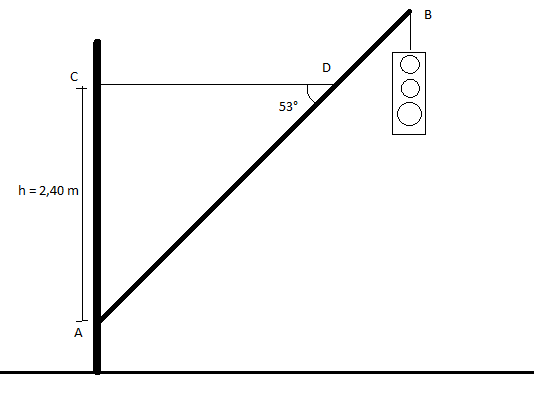
De oefening luidt :

Een verkeerslicht hangt aan een schuine paal zoals op de figuur afgebeeld. De homogene paal AB is 4,5 m lang en heeft een massa van 35,0 kg. De massa van het verkeerslicht bedraagt 10,0 kg. Bereken de spankracht in de horizontale massaloze kabel CD en bereken de beide componenten van de kracht die de paal AB uitoefent op het scharnierpunt A.

Als we de spankracht berekenen via moment (ik ga niet alles uitschrijven):



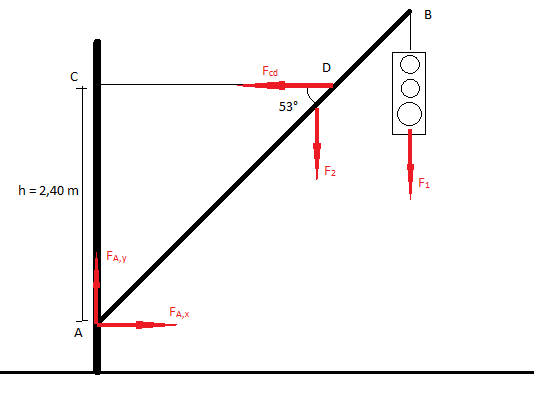
Check dit even : door mij berekend : loodrechte afstand van massamiddelpunt (2,25 m op paal) paal tot scharnierpunt A = 1,35 m en de loodrechte afstand van punt B tot A = 2,70 m.

(het moment wordt berekend met wijzerzin = + en tegen wijzerzin = - , ik weet dat dit anders afgesproken is op het forum maar toch omdat ik niet veel tijd heb, daarom ook geen berekeningen bij de loodrechte afstanden)

350 N * 1,35 m + 100 N * 2,70 m - Fcd * 2,40 m = 0

Fax = Fcd = 309 N

Als we de spankracht berekenen via ontbinden in krachten :

Fay = 100 N + 350 N = 450 N

dan bereken ik via tangens de Fax kracht omdat ze samen zorgen voor de krachten die de muur levert

tan(53°) = Fay/Fax

<=>

Fax = Fay/tan(53°)

= 450/1,327

= 339 N

Kan iemand vertellen waarom hier een verschil bestaat of wat ik fout doe?

[oktagon]

ff snel:

De eerste vergelijking met hoekwaarden lijkt me goed voor de trekstang. en die is ,zoals je verder berekent gelijk aan de druk hor. onder.

Het volgende verhaal wekt verwarring om wegens de hoekberekening:

tan(53°) = Fay/Fax

<=>

Fax = Fay/tan(53°)

= 450/1,327

= 339 N

Ook dit laatste lijkt me qua berekening goed;duik er nog eens opnieuw in;het geintje zit wel in de hoekberekeningen!

[Alopex]

offtopic : misschien past deze topic beter in het subforum Klassieke Mechanica, kan iemand van de moderators dit even doen?

[Alopex]

De hoekberekening gaat alsvolgt :

Er wordt aangenomen dat de kabel perfect horizontaal hangt denk ik.

aangezien de Fax ook loodrecht op de muur staat mogen we stellen dat de rechte AB twee evenwijdige rechten snijdt. Dit heeft als gevolg dat de hoek tussen AB en Fax ook 53° moet zijn (basiswiskunde).

Fay en Fax bepalen samen een resultante dus we mogen in rechthoekige driehoeken werken met tangens, cosinus en sinus regels.

regel : tangens = overstaande rechthoekszijde / aanliggende rechthoekszijde

en dan

tan(53°) = Fay/Fax

<=>

Fax = Fay/tan(53°)

= 450/1,327

= 339 N

[oktagon]

Als ik het effect van beide krachten op A bekijk,zou wegens het knooppunt bij D er een opwaartse kracht van 5 kg ontstaan naar boven (vert.) gericht en oplegreactie van 5 kg naar onder.Hierdoor zou er een lagere totale oplegreactie optreden van 300 N en dus niet passen bij de aansluitingshoek.

Zou alleen kunnen kloppen als de hoek A een vaste hoek is en geen scharnier en er een inwendig moment optreedt door die 10 kg (via het knooppunt D) en daar een hoekverdraaiing veroorzaakt van 37-> 34.5 = 2.5 graden en dat ook doet bij het knooppunt D van 53->55.5 = 2.5 graden (tg 55.5 = 450/309)

Probeer dat eens uit,tís jouw pakkiean!

[Alopex]

Maar in welke van de twee methoden zit er dan een fout? Die van de evenwichten of die van het ontbinden in krachten of in geen van beide?

[oktagon]

Ik weet daar geen antwoord op (hoewel ik er enkele uren in het uitwerken van krachtenschemas aan besteedde) en ben benieuwd of er onder de bezoekers en/of het moderatum deskundigen tevoorschijn willen komen om de TS te assisteren in het zoeken naar de juiste oplossing

[Alopex]

Toch alvast bedankt

Het zou zo moeten zijn dat de resulterende kracht van de muur op de paal en het verkeerslicht niet in het verlengde/richting van de paal ligt en dus een andere hoek maakt met de loodrechte op de muur.

De spankracht Fcd valt dus alleen maar te berekenen via moment (1ste methode) en niet via ontbinden in krachten omdat daar die hoek voor nodig is.

Ik hoop dat dit de juiste uitleg is. Kan iemand me daar in bevestigen of niet?

[dirkwb]

Check dit even : door mij berekend : loodrechte afstand van massamiddelpunt (2,25 m op paal) paal tot scharnierpunt A = 1,35 m en de loodrechte afstand van punt B tot A = 2,70 m.

Hier snap ik helemaal niets van. Loodrechte afstand van A tot B? |AB| = 4.5m

[aadkr]

Je stelt dat Fay /Fax =tan 53 graden.

Dat klopt volgens mij niet.

Inpunt A werken 2 reactiekrachten op de schuine paal van 4,5 meter lang.

Een vertikale kracht omhoog van 450 N

Een horizontale kracht naar rechts van 309 N

De resulterende kracht die op de onderkant van die schuine paal van 4,5 meter lang werkt is dus

545,87 N

De hoek die deze resulterende kracht maakt met de horizontaal is dus 55,52 graden

[Alopex]

Hier snap ik helemaal niets van. Loodrechte afstand van A tot B? |AB| = 4.5m

Misschien had ik mij wat duidelijker moeten uitdrukken. Wanneer we een moment moeten berekenen M = F.d dan is d altijd de loodrechte afstand uit het draaipunt op de werklijn/richting van de kracht. (de rechte door het draaipunt die loodrecht op de werklijn van de kracht staat)

Een horizontale kracht naar rechts van 309 N

Deze kracht heeft u, neem ik aan, berekend met moment? Zo niet hoe anders?

[aadkr]

De algebraische som van de momenten t.o.v. puntA moet nul zijn.

[oktagon]

Hier snap ik helemaal niets van. Loodrechte afstand van A tot B? |AB| = 4.5m

TS bedoeld de afstand van A naar de verticale werklijn van de kracht uit B = cos 53 * 4.50 = 2.70 m

[oktagon]

Je stelt dat Fay /Fax =tan 53 graden.

Dat klopt volgens mij niet.

Inpunt A werken 2 reactiekrachten op de schuine paal van 4,5 meter lang.

Een vertikale kracht omhoog van 450 N

Een horizontale kracht naar rechts van 309 N

De resulterende kracht die op de onderkant van die schuine paal van 4,5 meter lang werkt is dus

545,87 N

De hoek die deze resulterende kracht maakt met de horizontaal is dus 55,52 graden

Het probleem hier is ,dat de resulterende reacties bij A niet overeenkomen met de de hoek van 53 graden van de constructie.De reacties geven een hoek van 55...graden weer en dat is het conflict in deze topic en ik meen dat de invloed van de 10 kg aan de top een doorbuiging veroorzaakt in de lange staaf van 450 cm,doordat de hor. trekkabel fungeert als een soort steunpunt en in A een tegengestelde vert.reactie geeft van 50 N.Met als gevolg een afwijking van de 53 graden door de componenten bij A.