Hoogte achtbaan

[christopheb]

Hoi,

Ik probeer een examenvraag op te lossen in verband met de hoogte van een achtbaan. De vraag gaat als volgt:

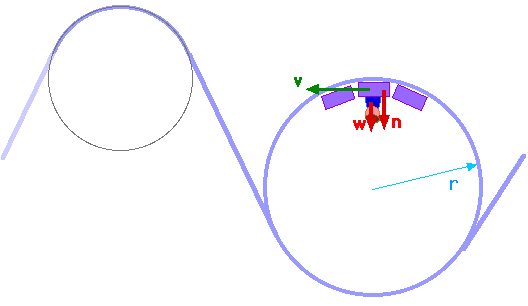
Wij beschouwen een achtbaan met een wagentje die enkele passagiers vervoert, zoals gegeven in Figuur 2. Wagentje en passagiers hebben een totale massa van 500kg. Het wagentje wordt losgelaten vanuit rust vanaf een hoogte h, die gemeten t.o.v. de minimale hoogte van de achtbaan is. Het wagentje beweegt wrijvingsloos en de achtbaan bevat een lus in het verticale vlak met straal R = 3 m.

Op welke hoogte moet de wagen vertrekken zodat de passagiers zich gewichtsloos voelen (geen netto kracht) op de hoogste punt van het lus?

Ik dacht dit te berekenen als volgt:

\(E_p = mgh\)

(potentiële energie in het begin van de rollercoaster)

\(E_k = \frac{mv^2}{2}\)

(kinetische energie op het moment dat het wagentje de lus in gaat gaan)

\(v^2 = 2gh\)

De totale kracht in de lus bovenaan is dan:

\(F_{tot} = F_{centripetaal} - F_{normaal} = 0\)

(Ik dacht dat de normaalkracht tegengesteld was aan de negatieve zwaartekracht in dit geval?)

\(F_{centripetaal} = F_{normaal}\)

\(\frac{m2gh}{r} = mg\)

\(\frac{2h}{3} = 1\)

\(h = \frac{3}{2}\)

Nu lijkt het mij nogal raar dat je maar van 1.5m hoogte moet vertrekken om door een lus met straal 3m te kunnen gaan. Is dit een plausibel antwoord? En heb ik mijn krachten ook correct bekeken?

[dirkwb]

\(mg \Delta h = mg(2r) + \frac{1}{2} mv^2 \)

Op het hoogste punt van de looping geldt:

\( mg =\frac{mv^2}{r} \rightarrow v^2 =gr \)

Dus

\( \Delta h = 2r + \frac{1}{2}r = 2.5r \)

[christopheb]

Hmm, blijkbaar had ik het behoud van energie op de foute plaats toegepast.

De bijvraag gaat als volgt: "Hoe groot is de normaalkracht op het wagentje in het onderste punt van de lus als het van deze hoogte vertrekt?"

Nu, de normaalkracht is toch onafhankelijk van de snelheid of hoogte? Mijn antwoord zou zijn:

\(Fn = -mg\)

[JorisL]

Als het niet gewoon de normaalkracht betreft die je aan geeft, wat zou er dan nog meer kunnen zorgen voor een kracht in een lus? Denk aan het soort beweging dat daar begint.

[christopheb]

Als het niet gewoon de normaalkracht betreft die je aan geeft, wat zou er dan nog meer kunnen zorgen voor een kracht in een lus? Denk aan het soort beweging dat daar begint.

Ik snap je vraag niet goed. Bedoel je dat er ook een centripetale kracht inwerkt?

Verder blijf ik het hele concept van de achtbaan heel vaag vinden. Zie bv deze tekening

Stel nu dat we gewichtsloosheid hebben, en de normaalvector gelijk is aan 0. Waarom valt het bakje dan niet naar beneden? Als ik het goed begrijp is de centripetale kracht, de kracht die nodig is om een object in uniforme rechte beweging af te buigen naar binnen in de cirkel toe. Dan zou dus het bakje vallen als de krachten die inwerken op het bakje groter zijn dan de centripetale kracht, en zou het bakje van de baan vliegen als de totale kracht die inwerkt kleiner is dan de centripetale kracht.

Dus het bakje valt als

\(F_n + F_z > F_c\)

. Is dit correct?

[Jan van de Velde]

Hou in de gaten dat "de" centripetaalkracht an sich niet bestaat. Er zullen altijd werkelijke krachten moeten zijn met naar het midden gerichte componenten, en die kunnen dan een centripetale kracht vormen.

Dus het bakje valt als

\(F_n + F_z > F_c\)

. Is dit correct?

Als het bakje valt is het los van de achtbaan, en zal er dus sowieso geen normaalkracht meer zijn toch? Dat constateerde je al:

Stel nu dat we gewichtsloosheid hebben, en de normaalvector gelijk is aan 0.

Bovenin de baan wijst F_z precies naar het middelpunt; als F_z dán groter is dan de benodigde centripetaalkracht voor dié cirkelbaan en dié snelheid, dan kan de achtbaanbeheerder beter even Apeldoorn bellen.