\(\rr\)
op het interval \(\langle 0,1 \rangle\)
overaftelbaar is.Met andere woorden: Je kunt niet alle elementen/waarden binnen dat interval afbeelden op een element van
\(\nn\)
.[/color]Of nog anders gezegd: je kunt niet alle elementen 'tellen'.
Verbeter me alsjeblieft hier al als ik dit fout heb; ik ben pas sinds deze avond 'bekend' met het begrip (over)aftelbaarheid en kardinaliteit.
Via Google vond ik een mooie en duidelijke uitleg van "Dr. Math" over waarom alle waarden van de verzameling
\(\qq\)
te tellen zijn: aftelbaar zijn. Zie hier:[/color]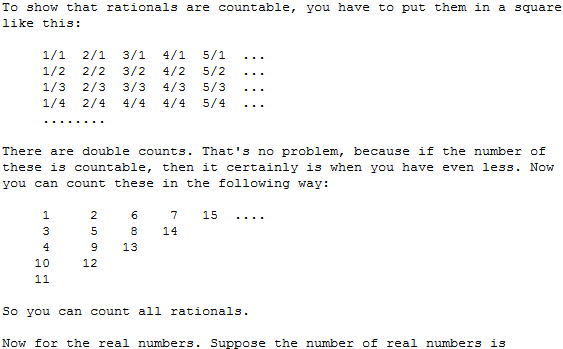
Bron: http://mathforum.org/library/drmath/view/52830.htmlhttp://mathforum.org/library/drmath/view/52830.html
Dit zette iemand anders en vervolgens mij aan het denken. Want, als je zo'n mooie manier mag verzinnen om álle elementen van
\(\qq\)
te kunnen noteren, om vervolgens te kunnen zeggen dat het evenveel elementen bevat als \(\nn\)
... Waarom geldt dat dan niet, als je alle elementen van
\(\rr\)
binnen het interval \(\langle 0,1 \rangle\)
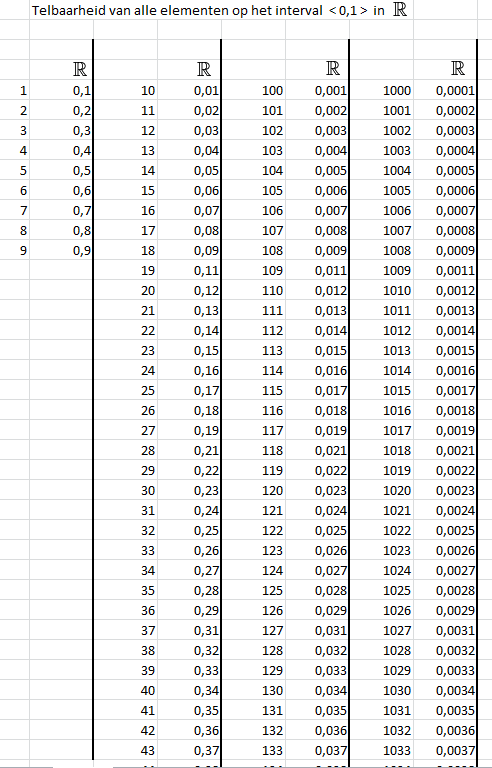
op een overzichtelijke manier noteert?[/color]Want, ja... Ik vind dat als jullie me maar genoeg tijd geven, ik álle elementen daarvan kan noteren.
Ik heb alvast een beginnetje gemaakt en als je het echt heel erg op prijs stelt, dan maak ik hem af tot ik alle elementen heb genoteerd.
Je zult dan zien dat elk element nog steeds te tellen is.
Dus ik stel: De verzameling van
\(x \epsilon \rr \)
| \(0<x<1\)
bevat evenveel elementen als \(\nn\)
(zo noteer je dat toch?)[/color]Mijn vraag aan jullie:
Willen jullie me vertellen waar ik hier een foute maak in m'n gedachten? Waarom klopt het niet wat ik zeg?
Hieronder mijn beginnetje aan het noteren van al die elementen: