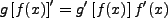Les 2a : Maxima / Minima
In deze les gaan we bekijken hoe je via differentiëren minimale en maximale waarden van een functie kunt vinden, ook wel extreme punten of "extremen" genaamd.
Hier vast in het kort de werkwijze waar we naartoe werken, daarna volgt de uitleg:
- Bepaal f'(x)
- Bereken de nulpunten van f'(x)
- Maak een tekenschema van f'(x)
- Lees de minima en maxima af
Inleiding: wat zijn minima en maxima?
Een minimum of maximum van een functie is een punt waar de functie een zo klein of groot mogelijke waarde aanneemt. In de grafiek van een functie komt dat overeen met een berg of een dal. Voorbeeld:
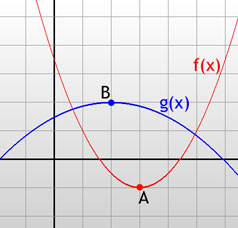
Punt A is hier een minimum van de functie f.
Net zo is punt B een maximum van g.
Lokaal
Heel vaak gaat het om
lokale minima en maxima, dat wil zeggen dat zo'n punt minimaal of maximaal is
voor de omgeving van dat punt. Voorbeeld:
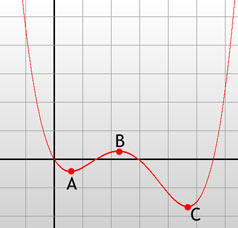
De punten A en C zijn hier allebei lokale minima, en punt B is een lokaal maximum. Hoewel de functie verderop nog groter wordt dan B, en rondom C ook lager ligt dan in A, noemen we de punten wel
lokale minima en maxima, omdat de functie in de buurt van die punten daar minimaal of maximaal wordt.
"In de buurt" moet je opvatten als dat er een gebiedje om zo'n punt heen ligt (ook al is het een heel klein gebiedje) waarbinnen dat punt minimaal of maximaal is.
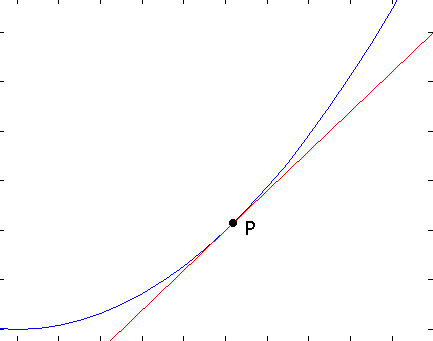
Helling, raaklijn en afgeleide
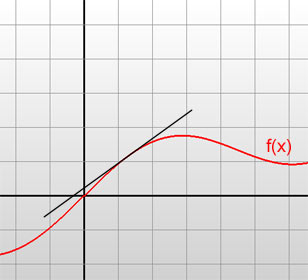
Nu bekijken we een grafiek van een andere functie, waarin een minimum, een maximum, en enkele raaklijken staan aangegeven:
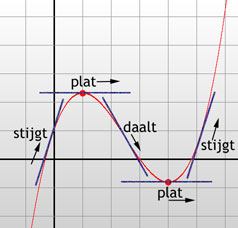
Zoals je ziet stijgt de functie links van een maximum, en daalt hij rechts ervan. En bij een minimum omgekeerd. Op de extreme punten zelf is de grafiek plat. Dat is logisch, als de functie in een bepaald punt stijgt of daalt (dus niet plat is) ligt de grafiek ietsje naast dat punt altijd hoger, en aan de andere kant lager, en dus zou dat punt ook geen minimum of maximum zijn.
In het volgende plaatje staat in het blauw de grafiek van f'(x):
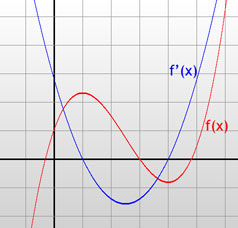
Zoals je weet en wellicht in het plaatje ook kunt zien, is f'(x) de helling van f(x). Dus hoe groter f'(x), hoe steiler f(x) oftewel hoe harder f(x) stijgt, en hoe kleiner (negatief) f'(x) is, hoe harder f(x) daalt. Als f'(x) nul is, dus waar zijn grafiek door de x-as gaat, is de grafiek van f(x) plat: een helling van nul betekent geen stijging of daling. Je ziet in het plaatje dat dit het geval is in x=1 en x=4.
De platte stukken van f(x), en dus de (mogelijke) minima en maxima van f(x), komen dus overeen met de nulpunten van f'(x)!
Nu maken we iets wat we een
tekenschema van f'(x) noemen: we geven de nulpunten aan, dat wil zeggen de x'en waarvoor f'(x)=0, en er tussenin geven we aan of f'(x) daar positief (+) of negatief (-) is:
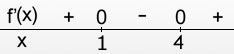
Aan zo'n tekenschema kun je nu de minima en maxima van f(x) uitlezen! Let op: een nulpunt
kan een extreem punt zijn, maar dat hoeft niet! Als het teken links van het nulpunt anders is dan rechts, dan heb je te maken met een minimum of maximum.
Als f'(x) links van het nulpunt positief is en rechts negatief, dan steeg de functie f(x) dus eerst en daarna daalde hij weer, dus is het nulpunt van f'(x) een
maximum van f(x). Als f'(x) links daalde, en rechts weer steeg, dan is het nulpunt van f'(x) blijkbaar een
minimum van f(x).
Je kunt ook zo'n situatie hebben:
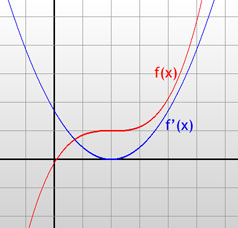
Het bijbehorende tekenschema is:
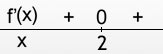
Hier zie je dat f'(2) weliswaar 0 is, dus op x=2 ligt een nulpunt van f'(x), maar zowel links als rechts van het nulpunt is f'(x) positief! De functie f(x) stijgt dus, stopt dan even in één punt (in x=2) met stijgen, en stijgt daarna weer verder. In dat geval is er dus géén sprake van een minimum of maximum!
De algemene werkwijze bij het bepalen van extreme punten van een functie zal nu wel duidelijk zijn:
- Differentieer de functie, zodat je in ieder gewenst punt de helling kunt bepalen.
- Zoek de nulpunten van de afgeleide, hier kunnen zich mogelijk minima en maxima bevinden.
- Zet een tekenschema op, geef de nulpunten aan, en bepaal het teken (+ of -) van de afgeleide in de tussengelegen gebieden. Dit doe je door gewoon een willekeurig tussenliggend punt in f'(x) in te vullen: als f'(x) bijvoorbeeld nulpunten heeft op x=0 en x=5, vul je x=1 of x=2 of x=pi.gif of wat dan ook in, alles wat tussen 0 en 5 ligt is goed om het teken van f'(x) te bepalen in dat gebied.
- Bekijk nu of er nulpunten zijn waar f'(x) van teken wisselt: links + en rechts - is een maximum, omgekeerd is een minimum. Aan beide kanten hetzelfde teken wil zeggen: geen mimimum of maximum.
Een voorbeeld
Bepaal van de functie f(x) = x
3-9x
2+15x-4 de lokale minima en maxima.
Oplossing:
Eerst differentiëren: f'(x) = 3x
2-18x+15
Nulpunten van f'(x) uitrekenen: f'(x) = 3x
2-18x+15 = 0, dit los je op door hem te herschrijven naar 3(x-1)(x-5) of desnoods met de abc-formule, de oplossingen zijn x=1 en x=5.
In het tekenschema vullen we uit ieder gebied (dus x<1, 1<x<5, en x>5) een willekeurige waarde in om het teken te bepalen.
Bijvoorbeeld f'(0) = 15 = positief, f'(2) = -9 = negatief, f'(6) = 15 = positief.
Het tekenschema wordt dus:
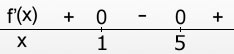
Conclusie: f(x) heeft een maximum op x=1, en een minimum op x=5.
De waarden in deze extreme punten krijg je door deze x'en in f(x) in te vullen: f(1)=3 en f(5)=-29.
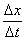
 wordt gebruikt om een verschil aan te duiden. In dit voorbeeld is de snelheid van de auto dus 100 m / 10 s = 10 m/s.
wordt gebruikt om een verschil aan te duiden. In dit voorbeeld is de snelheid van de auto dus 100 m / 10 s = 10 m/s.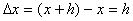
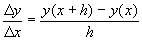
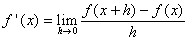
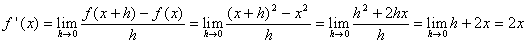






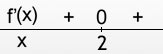

 (1)
(1)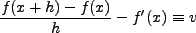 (2)
(2) (3)
(3) (4)
(4)