Les 2(b) : Maxwell's theorie verder uitgewerkt
'Albert Einstein ' schreef:"The most profound and most fruitful that physics has experienced since the time of Newton."
Dit hierboven is een quote van Einstein over het werk van Maxwell. Door hier mee te beginnen is meteen duidelijk of Maxwell nou iets voor de relativiteit heeft betekend.
Maxwell was een Schotse wiskundige, die natuurkundige problemen op een wiskundige manier aanpakten. Voordat hij zijn werk totaal aan elektro- en magnetisme besteedde had hij al enkele rapporten geschreven over thermodynamica, kinematica en mechanische deformaties.
Dit hoofdstuk gaat over de formules van Maxwell, en gaat dus verder als hoofdstuk 2a. Voor het begrijpen van de relativiteitstheorie is het niet erg om dit hoofdstuk over te slaan. Hoofdstuk 2a en 2b gaan over het zelfde onderwerp en zijn appart van elkaar te lezen.
Aan het eind van dit hoofdstuk begrijp je dat uit de formules van Maxwell geconcludeerd wordt dat lichtsnelheid een Elektro-Magnetische golfbeweging is. De snelheid van deze golfbeweging is constant en wordt de lichtsnelheid genoemd. De afleiding van de formules van Maxwell zijn vrij wiskundig, ook is een voorkennis over Elektro-Magnetica gewenst.
Vier van de staande fundamentele vergelijkingen over de Elektro-Magnetica onderwerp worden hier verder uitgelegd.
De wet van Gauss over het Elektrisch veld
Gauss introduceerde een nieuwe grootheid in het veld van de elektrostatica. De Elektrische Flux. De E-flux is het elektrische veld dat loodrecht door een oppervlakte gaat. Voor de wet van Gauss bekijken we de flux door een gesloten oppervlak zoals een bol of een aardappelvorm, wiskundig gesproken:
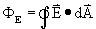
Dat rondje in de integraal betekend dat het een oppervlakte is zonder eind, bijvoorbeeld een bol, of een aardappel.
Nu is dat voor aardappelvormige voorwerpen wat moeilijk uit te rekenen, dus laten we de versimpelde vorm van een bol nemen. In het middelpunt van deze bol bevindt zich een lading ‘q’ door symetrie is er op elke plaats op de holle bol het zelfde E-veld.
De elektrische flux door de gesloten oppervlakte van de bol is als volgt:
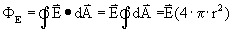
Het E-veld ten gevolge van een lading is als volgt:
(Q is lading, en r is afstand, maar wat is k?)
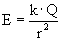
Vullen we dit in krijgen we de E-flux die totaal niet afhankelijk is van de diameter van de bol
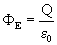
Hieruit kunnen we stellen dat deze vergelijking voor alle afgesloten oppervlaktes geldt. Dus ook voor aardappelvormen. De eerste wet van Gauss is:
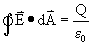
De wet van Gaus over het Magnetisch veld
Het vorige gedachtenexperimentje voerde Gauss ook uit op het Magnetisch veld. Eerst werd de Magnetische flux bepaald zijnde het magnetisch veld loodrecht door een oppervlak. Wederom ging hij van een gesloten oppervlak uit.
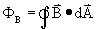
We nemen nu een puntbron van een magnetisch veld in een holle bol. En dan hebben we een probleem. Er is namelijk niet zoiets als een magnetische lading. Iets wat magnetisch is, heeft altijd een positief en een negatief magnetische kant. Het positef magnetisch veld is daarbij even groot als het negatieven. Plaatsen we nu de magnetische puntbron in een holle bol, dan kunnen we wel bedenken dat de som van het M-veld door de opp. Van de bol nul moet zijn. Vandaar:
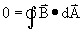
Dat dit voor alle gesloten oppervlakten moet gelden weten we omdat het magnetisch veld zoals ook bij het E-veld kwadratisch vermindert m.b.t de afstand.
Epsilon en Mu
De vorige twee vergelijkingen zijn bedacht als zijnde in het vacuum. We weten dat bepaalde stoffen de eigenschappen hebben om een magnetisch veld of elektrisch veld te absorberen. Dit geven we aan met een constante. Deze constante geeft aan hoe veel meer de stof de creatie van het elektrisch of magnetisch veld tegen gaat. Voor vacuum zijn deze constanten als volgt vast gesteld:
ε0 = 8.85 · 10-12
μ0 = 1.26 · 10-6
Voor andere stoffen drukken we de constante uit in een veelvoud van de constanten hierboven. Vacuum is dus 1.
In al onze vergelijkingen kunnen we deze constanten vervangen door hun waarden in een ander medium, zoals water.
Faraday’s wet m.b.t het elektrisch veld
De basis van Faraday’s wet voor het genereren van een inductiespanning is dat een spanning wordt gevormd als het magnetisch veld door een afgesloten ring verandert.
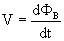
Waarbij V spanning is. Spanning is weer niets anders dan de som van het E-veld over de afstand, s, tussen bron en punt-van-interesse.
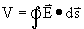
Faraday’s wet beschrijft de creatie van een inductiespanning bij een veranderende magnetische flux:
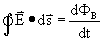
Ampêre’s wet m.b.t het magnetisch veld
Ampêre’s wet beschrijft de creatie van een magnetisch veld rond een elektrische stroom. Gauss had al ontdekt dat er niet een magnetische monopool bestaat. Een magnetisch veld wordt dan ook gegenereert door een elektrische stroom.
Als bijvoorbeeld door een stroomdraad een stroom loopt, loopt er een magnetisch veld loodrecht op deze stroomdraad. Het bewegende elektron creëert een magnetisch veld.
Ampêre vond dat de gesloten integraal van het magnetisch veld over een (imaginaire) gesloten kring, wat we dus de magnetische flux noemen, gelijk is aan de stroom die loodrecht door deze kring gaat, maal de constante van magnetische premeabiliteit.
Wiskundig uitdrukt:
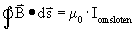
Om nu te bepalen of een stroom positief of negatief is, gebruiken we de rechterhand regel.
(Hoe gaat deze regel ook al weer?)
Maxwell’s contributie aan de vergelijking van Ampêre
De wet van Ampêre had voor Maxwell een ongelijkheid in de vergelijking.
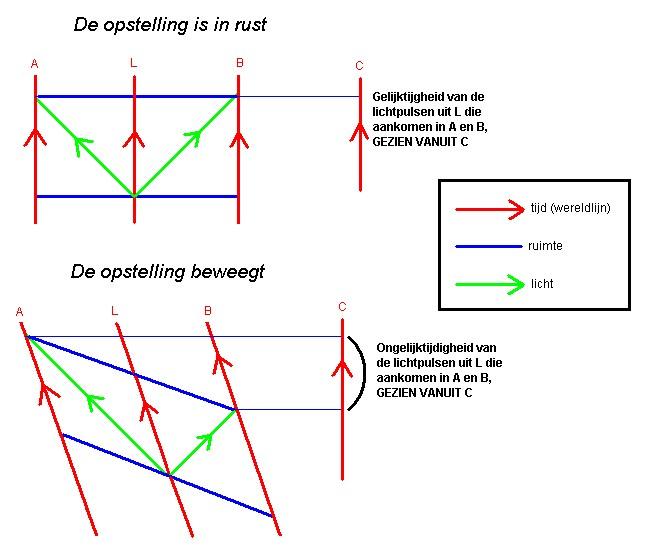
Omdat de oppervlakte omringd door de kring waarover geintegreerd wordt niet wordt gespecifieerd. Stel voor dat de stroom door de draad een condensator op laad. Het oppervlakte waarover geintegreerd wordt kan een schijf loodrecht op de draad zijn, dan geldt de wet van Ampêre gewoon. Het kan echter ook een bolvormige schijf betreffen, waarbij het oppervlakte over de capaciteit valt, zie de tekening.
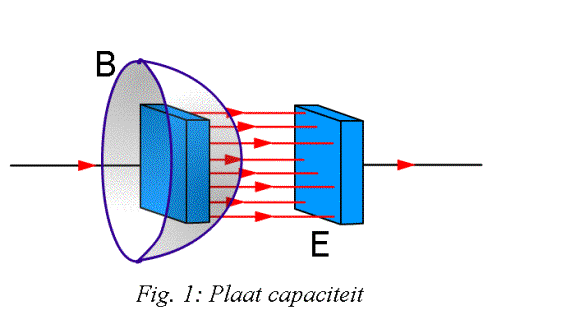
Een capaciteit is echter een vreemd iets, zonder dat er echt een stroom loopt wordt er toch een stroom geïnduceerd aan de andere kant van de capaciteit. Faraday beschreef dit effect als zijnde dat de lading verplaatst werd, tussen de twee capacitaire platen, door de “ether”. We weten nu dat er een lading wordt geinducerd op de andere capacitaire plaat. Dit induceren werd niet verklaart door Ampêre.
Volgens Maxwell geldt dus:
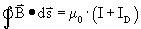
Waarin ID dus de ‘stroom’ is die door de ether loopt. Maxwell begreep dat de elektrische veldsterkte groter werd omdat er een lading opbouw op de twee capaciteitplaten plaats vond. De bekende formule voor elektrische veldsterkte van een plaat-capaciteit is:
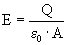
Hieruit leiden we af dat de verandering van lading ofwel de stroom:
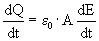
In het voorbeeld van de plaat-capaciteit is de elektrische flux ΦE = E·A vandaar:
(Klopt dit wel? Wat is de elektrische flux tussen de platen van een plaatcondensator?)
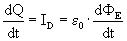
Maar deze varierende flux zou ook effect moeten hebben op het gecreeerde magnetisch veld. De aangepaste wet van Ampêre wordt dus:
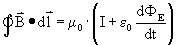
Let wel, dit geldt alleen als de capaciteit aan het opladen is, anders is dQ/dt = 0 en loopt er in feite geen stroom meer:
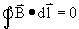
zoals Ampêre het voorspelde.
Wat belangrijk is, is dat bij wisselende E-velden, een magnetisch veld kan ontstaan binnen in een capaciteit, dus in deze zogenaamde “ether”.
Laten we de vier vergelijkingen nog eens in een lijstje zetten:
Gauss
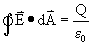
Gauss
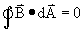
Faraday
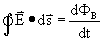
Ampêre-Maxwell
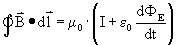
(Scroll terug naar de betreffende vergelijking voor meer informatie)
Golf-vergelijking
De bekende vergelijking uit de mechanica voor een golfverschijnsel is als volgt:
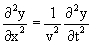 (Wie kan dit aantonen?)
(Wie kan dit aantonen?)
Nu was rond de tijd van Maxwell al wel duidelijk dat licht een golfverschijnsel is, en zal dus de golfvergelijking ook voor licht wel toepasbaar moeten zijn, immers moet de “ether” toch ook voor een bepaalde impuls overdracht van de trillingen zorgen?
Om van de 4 vergelijkingen van Maxwell de vergelijking voor licht te deriveren moeten we diep in de Wiskunde gaan, Maxwell was namelijk een wiskundige, en tot groot ergenis van elk fysicus is zijn theorie verstoken van de wiskundige vergelijkingen.
Wiskundige afleiding Maxwell vergelijkingen
We gaan verder net na het bepalen van de elektro-magnetische formules.
Om het niet te ingewikkeld te maken nemen we wel een paar aannamens.
Wat wel duidelijk zal worden, is dat vanuit de elemantaire elektro-dynamische vergelijkingen van Maxwell een vergelijking voor het licht zal blijken. Ook zal blijken dat de snelheid van het licht afhankelijk is van de magnetische en elektrische eigenschappeen van het medium.
Aannamen 1. We bevinden ons in de vrije ruimte. Alle ladingen bevinden zich ver weg. Door de aannamen kunnen we stellen dat de E-wet van Gauss nul is. Het oppeervlakte waarover geintegreerd wordt is namelijk ontzettend groot, daardoor is E erg klein, gaat naar nul.
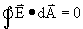
Aannamen 2. Een wisselend magnetisch veld genereert een wisselend elektrisch veld genereert een wisselend magnetisch veld genereerte een wisselend elektrisch veld, enz. enz.
Deze aannamen is ook wel uit de wet van Faraday en Ampêre-Maxwell te halen daar Faraday verklaart dat een wisselend magnetisch veld een elektrisch veld op levert. En Ampêre-Maxwell verklaart dat (mede) een wisselend E-veld een Magnetisch veld creeert. Nemen we nu niet de moeite om dit ook aan te tonen.
Stelt u zich twee wisselende golfbewegingen voor, de ene is het E-veld en beweegt zich in de y-richting, de andere is het M-veld en beweegt zich in de z-richting. De trilling vervolgd zijn weg parallel aan de x-as. Zie figuur 2.
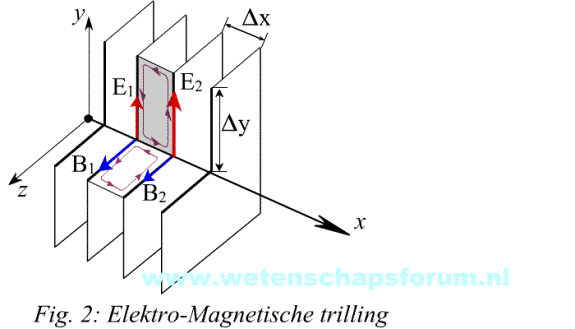
Omdat we Δx als heel klein beschouwen mogen we aannemen dat de magnitude van het E- en M- veld constant zijn en alleen varieren in de x-richting. E1, E2, B1 en B2 zijn constant.
Als eerste passen we de wet van Faraday toe op het grijze vierkantje over Δx en Δy. De lijn integraal bestaat uit 4 delen. Voor de integraal over dx hebben we E·dl = 0 omdat E loodrecht op dl (Δx) staat. De andere twee delen zijn:
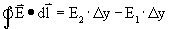
Door gebruik te maken van de rechterhand regel weten we dat de magnetische flux uit het oppervlakte waarover geintegreerd is, in positieve z-richting. De magnetische flux is als volgt:
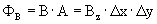
De verandering per tijd is:
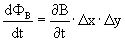
Het moet partieel gedifferentieerd worden omdat we de veranderende op één punt in de tijd willen weten, en we net hebben aangenomen dat daar E en B constant zijn. Voegen we deze vergelijkingen bij elkaar krijgen we:
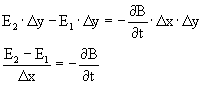
Als Δx enorm klein is wordt de vergelijking
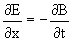
Deze werkwijze kan ook voor de Ampêre-Maxwell vergelijkingworden gemaakt. Dit doen we op het vierkantje Δx en Δz. Er loopt geen stroom, want we zitten in de vrije ruimte. We krijgen dan:
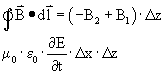
De richting van integreren wordt hier bepaald door de richting van het E (y-positief) en dus door de rechterhand regel.
(Krom je vingers rond de cyclus van B en je duim wijst omhoog.)
Door de laatste formule wiskundig wat op te knappen krijgen we:
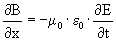
Wat we nu dus hebben gedaan is gebruikmakend van onze aannamens de wetten van Faraday en Ampêre omgeschreven naar een differentiaal vergelijking:
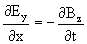
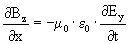
Nu zou het fijn zijn als we een vergelijking krijgen waarin of alleen E, of alleen B staat. Dit doen we d.m.v beide zijden te differentieren:
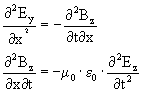
Deze laatste stap lijkt erg plastisch. Het is wiskundig toch gegrond omdat na het “extra” differentieren de vergelijkingen nog steeds kloppen.
Deze actie is ook uit te voeren zodat de E-termen wegvallen en men het volgende overhoudt:
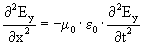
De Maxwell vergelijkingen
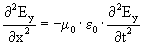
Voor het magnetisch veld:
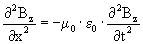
Als we deze vergelijking met de bekende mechanische golfvergelijking vergelijken zien we dat de snelheid van de trilling als volgt is.
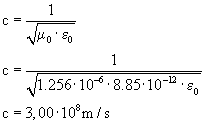
Dit is de snelheid van licht in vacuum, van een vorige paragraaf weten we dat dat epsilon (ε) en mu (μ) vervangen kunnen worden door de epsilon en mu van een bepaald medium.
De snelheid van licht door een medium ligt dus vast. Het is alleen afhankelijk van de elektromagnetische eigenschappen van dat medium.
Toen Maxwell in de 19de eeuw de waardes voor epsilon en mu invoerden, die niet helemaal nauwkeurig waren. Kwam hij uit op een lichtsnelheid van 3,10·10<sup>8</sup> m/s.
Dit is een fout van maar 3% op de toen bekende lichtsnelheid. Dit, samen met de theoretisch afleiding, was voor wetenschappers genoeg bewijs voor het aanvaarden van de theorie.
De zoektoch naar de ether begint
Maxwell en Faraday hadden aangenomen dat de elektrische (en magnetische) straling in een capaciteit wordt verplaatst door een medium: “de ether”. Maxwell toonde aan dat licht elektromagnetische stralingen zijn en dat de snelheid alleen afhankelijk is van de elektromagnetische eigenschappen van het medium. De ether zou dus ook voor de verplaatsing van licht moeten zorgen. Licht bereikt ons vanaf onze ster de zon door de ruimte, is de hele ruimte dus gevuld met een soort ether?
De wiskundige ondekking van Maxwell spoort de experimentele natuurkunde en sterrenkunde aan om de theorie van Maxwell te bewijzen en om de eigenschappen van de ether te bepalen. De zoektocht naar de ether uit zich in het beroemde Michelson en Morely experiment, daar gaat ons verhaal verder.
Het mogen duidelijk zijn dat de theorie van Maxwell wat stof deed oplaaien. We eindigen dit hoofdstuk gelijk als waarmee we het begonnen, met een quote van Einstein.
'Albert Einstein ' schreef:"The special theory of relativity owes its origins to Maxwell's equations of the electromagnetic field"
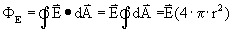
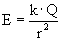
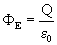
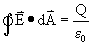
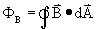
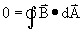
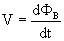
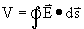
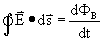
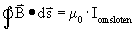

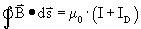
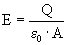
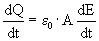
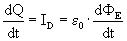
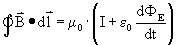
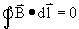
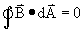
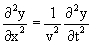
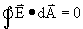

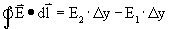
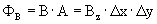
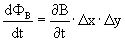
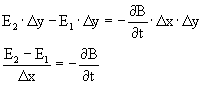
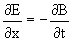
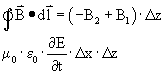
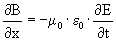
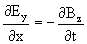
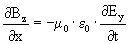
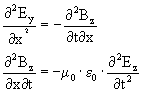
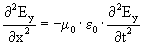
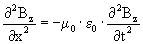
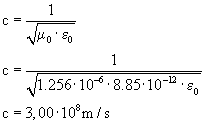
 -
- 
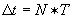 een heel aantal malen de trillingstijd T van het gebruikte licht is versterken de lichtbundels vanuit S1 en S2 elkaar weer in P.
een heel aantal malen de trillingstijd T van het gebruikte licht is versterken de lichtbundels vanuit S1 en S2 elkaar weer in P. 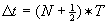 doven de lichtbundels elkaar juist uit.
doven de lichtbundels elkaar juist uit. 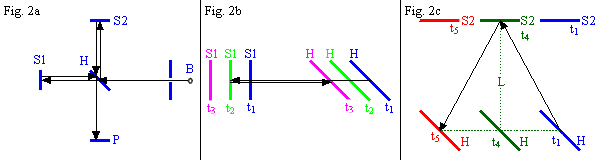
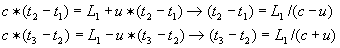
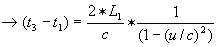
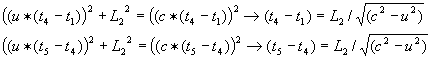
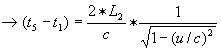
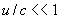 geldt
geldt 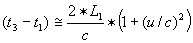 en
en 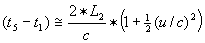
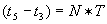 (een heel aantal malen de trillingstijd van het gebruikte licht) versterken de lichtbundels vanuit S1 en S2 elkaar.
(een heel aantal malen de trillingstijd van het gebruikte licht) versterken de lichtbundels vanuit S1 en S2 elkaar. 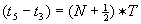 doven de lichtbundels elkaar juist uit.
doven de lichtbundels elkaar juist uit. 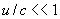 :
: 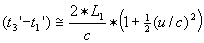 en
en 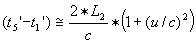
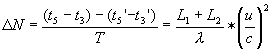
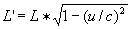

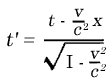
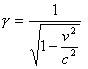
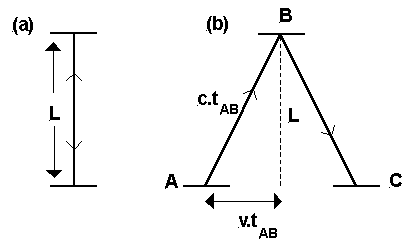
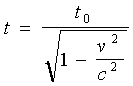
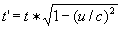
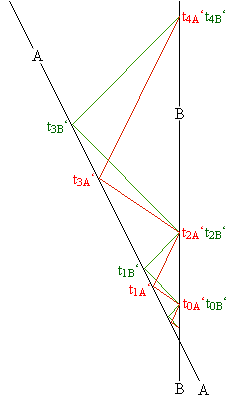
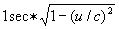 een lichtpuls ontvangt.
een lichtpuls ontvangt. 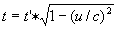 Dus de klok van zijn broer loopt langzamer. Dit klopt ook met wat hij meet: als hij met zijn broer afspreekt, dat die om de seconde een lichtflits zal sturen vindt hij, dat hij in feite om de
Dus de klok van zijn broer loopt langzamer. Dit klopt ook met wat hij meet: als hij met zijn broer afspreekt, dat die om de seconde een lichtflits zal sturen vindt hij, dat hij in feite om de 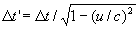 een lichtflits. Echter omdat de ruimteschepen ten opzichte van elkaar bewegen lopen opeenvolgende lichtflitsen voordat ze B bereiken een vertraging 1 (u/c)2 op. Hierdoor zijn de tijdsintervallen waarmee ze B bereiken zijn:
een lichtflits. Echter omdat de ruimteschepen ten opzichte van elkaar bewegen lopen opeenvolgende lichtflitsen voordat ze B bereiken een vertraging 1 (u/c)2 op. Hierdoor zijn de tijdsintervallen waarmee ze B bereiken zijn: 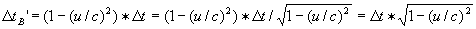
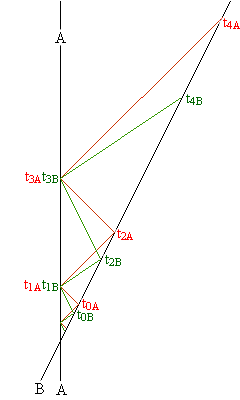
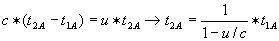
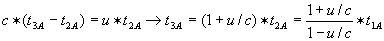
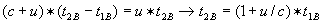
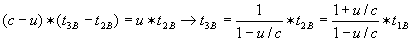
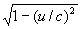 langzamer. Dus
langzamer. Dus 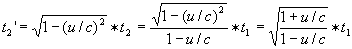
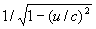 sneller. Dus:
sneller. Dus: 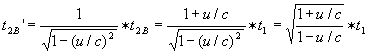
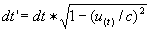
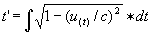
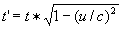
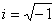 te gebruiken en wel T = i·c·t.
te gebruiken en wel T = i·c·t.