Rotatie - vliegtuig / raket zwaartepunt

[Arie Bombarie]

Goedendag,

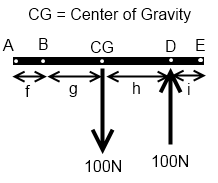
Wanneer een balk bevestigd is aan een scharnier, zal de balk roteren om dit scharnierpunt wanneer er een kracht op de balk wordt uitgeoefend (ervan uitgaande dat de kracht een resulterend moment veroorzaakt om de scharnier die niet gelijk is aan 0).

Bij een vliegtuig / raket is er echter niet sprake van een dergelijke fysieke scharnier. Een vliegtuig zal draaien om zijn center of gravity.

Quote (Nasa):

If the object is confined to rotate about some other point, like a hinge, we can still describe its motion. In flight, both airplanes and rockets rotate about their centers of gravity.

Echter, waarom is dit zo? Waarom roteert een vliegtuig niet om een punt dat 3cm verwijderd ligt van zijn center of gravity, of 2cm, of...?

Ik heb even een simpele schets gemaakt:



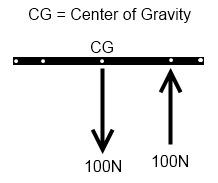
Dit is een vliegende balk ("vliegtuig") van homogeen materiaal waarvan het CG precies in het midden ligt. De resulterende zwaartekracht is 100N en is geplaatst op de locatie van het CG. Verder wordt er een kracht van 100N uitgeoefend op een bepaalde afstand van het CG.

De vliegende balk zal in deze situatie roteren om zijn CG, maar waarom?

Alvast bedankt!

[aadkr]

Je mag hier volgens mij de momentenstelling toepassen

[Arie Bombarie]

Hartelijk dank voor de reactie.

Bij deze:



Ik ga er vanuit dat momenten rechtsom positief zijn:

\(\sum M_{A}=-100*(f+g)+100*(f+g+h)\)

\(\sum M_{B}=-100*g+100*(g+h)\)

\(\sum M_{CG}=100*h\)

\(\sum M_{D}=100*h\)

\(\sum M_{E}=100*(h+i)-100*i\)

Ik zie echter (nog) niet hoe ik met deze gegevens kan vaststellen dat de balk om het CG zal roteren.

[Jan van de Velde]

Ik weet niet hoe ik dit elegant moet uitleggen. Maar laat ik eens ergens beginnen, dan schiet ons vast wel iets te binnen.

maar laten we eens een massaloze stok bedenken van 1,5 m lang. Aan het ene eind bevestigen we een puntmassa van 1 kg, aan het andere eind een puntmassa van 2 kg.

We leggen de stok dwars voor ons op een gladde tafel.

Jij weet feilloos aan te wijzen wáár je loodrecht tegen de stok moet duwen opdat de stok opschuift zonder dat de richting waarin de stok wijst verandert (dus zonder dat de stok gaat draaien):

arie1 747 keer bekeken

laat ons de zwaartekracht even uitschakelen, de stok rechtop zetten en er horizontaal een kracht op gaan uitoefenen.

arie2 746 keer bekeken

Kracht en versnelling zijn vectoriële zaken. Kracht horizontaal naar rechts betekent versnelling horizontaal naar rechts. En niet zomaar een of andere kant op. Mee eens?

Nu gaan we moeilijk doen:

arie3 746 keer bekeken

Is er iets veranderd aan "kracht horizontaal naar rechts betekent versnelling horizontaal naar rechts" voor de stok als geheel?

Deze "waarom" vraag verplaatst naar klassieke mechanica

[Arie Bombarie]

Hartelijk dank voor de reactie.

In de laatste situatie is er niets veranderd aan "kracht horizontaal naar rechts betekent versnelling horizontaal naar rechts" voor de stok als geheel. Er zal namelijk nog steeds een nettokracht op de staaf werken richting "rechts".

Wel zal er een rotatie optreden van de staaf om zijn CG (waarom per se zijn CG?), waardoor je kracht mogelijk meedraait (afhankelijk van de oorsprong van de kracht).

[Jan van de Velde]

Precies, de staaf als geheel zal dus een baan horizontaal naar rechts gaan volgen.

Hoe verklaren we nu elegant dat dat betekent dat het massamiddelpunt die rechte lijn naar rechts beschrijft, en onze beide massa's daaromheen draaien (want dat is wat er gebeurt)? Daar zit ik nog even mee.

[aadkr]

Laten we voor het gemak aannemen dat de vierkantjes in de tekening van Jan afmetingen hebben van 1 bij 1 cm

We zien in het laatste plaatje dat die blauwe kracht F horizontaal naar rechts wijst en aangrijpt op 2 cm boven het zwaartepunt.

Wat we nu mogen doen is het volgende.

We plaatsen in het zwaartepunt 2 even grote horizontale krachten die tegengesteld gericht zijn en een grootte hebben die gelijk is aan die blauwe kracht. Wat is nu de nieuwe situatie?

[shimmy]

Allereerst, ongetwijfeld al duidelijk, evident is dat het zwaartepunt (CG) het balanspunt is van een zwevend object. Een beetje zoals Jan al omschrijft met zijn stok op de gladde tafel, waneer je een vliegtuig met een enorme vinger zou kunnen ondersteunen en optillen zou het in balans blijven waneer je dit onder het zwaartepunt doet. Ook als je het vliegtuig op zou hangen aan twee horizontale touwtjes aan de zijkant van de romp bevestigd zou het alleen in balans zijn waneer die touwtjes ter hoogte van het zwaartepunt zitten. Zou het opgehangen vliegtuig nu 10 graden gedraaid worden zou het in die nieuwe stand weer in evenwicht blijven hangen.

Er zit even veel kracht*arm voor het zwaartepunt als er achter (zelfde geld voor even veel kracht*arm boven/onder en links rechts).

Waarom roteert een vliegtuig niet om een punt dat 3cm verwijderd ligt van zijn center of gravity, of 2cm, of...?

Simpel gezegd, weg van de minste weerstand. Het vergt de minste moeite om het vliegtuig (of een ander object) om zijn zwaartepunt te laten roteren.

Stel ik neem in wip in de speeltuin. Ik wil het in vast tempo op en neer doen bewegen. Ik heb geen keus, de wip draait om zijn schanier. Zit er nu op de ene kant van de wip een even zwaar kind als op de andere kant dan kost het relatief weinig moeite om de constante op en neer beweging vast te houden. Dit is omdat het schanier punt samen valt met het zwaartepunt. Loopt 1 kind later weg dan is het niet meer zo makkelijk om de constante snelheid vast te houden. Naar beneden moet je het kind de hele tijd afremmen en naar boven weer optillen. Jij zegt misschien, das logisch, kracht*arm is niet meer gelijk. Ik zeg: das logisch, het zwaartepunt valt niet meer samen met het schanier punt. Je draait nu niet meer om de CG maar om een punt dat verwijdert ligt van de CG.

[Arie Bombarie]

Excuses voor mijn erg late reactie, ik was dit topic helemaal vergeten.

Je bericht snap ik shimmy, je stelt echter:

Simpel gezegd, weg van de minste weerstand. Het vergt de minste moeite om het vliegtuig (of een ander object) om zijn zwaartepunt te laten roteren.

Het kost inderdaad de minste moeite om het vliegtuig om zijn zwaartepunt te laten roteren, maar waarom roteert het vliegtuig om het punt waarbij het het minste moeite kost om het te laten roteren? Waarom roteert het vliegtuig niet "gewoon" om een punt 1 meter links van het zwaartepunt maar dan met een lagere snelheid / acceleratie t.o.v. een rotatie rond het zwaartepunt?

[shimmy]

Maar, vraag jij je dan ook af waarom je als je tegen je openstaande autodeur aan duwt, de deur dicht valt in plaatst dat de deur open blijft staan maar je de hele auto naar achteren duwt. De weerstand van de deur om dicht te vallen is vele malen lager dan de weerstand van de auto om naar achteren te rollen, en daarom valt de deur dicht.

Daarom stroomt een rivier hoe hij stroomt, vliegt een auto wel of niet uit een te scherpe bocht en daarom draait het vliegtuig om zijn zwaartepunt.

[robairo]

De bewegingen van een vliegtuig worden alijd ontleedt in verschillende tov het zwaartepunt: stijgen/dalen accelereren/deceleren, gieren, pitch(=het draaien waar we het over hebben),

en we het het over de pure pitch hebben draait de pitch per definitie over over het zwaartepunt.

In werkelijkheid hebben we een optelling van de verschillende bewegingen en dat ziet er gecombineerd anders uit.

Als je allerlei krachten op een vliegtuig aanbrengt kan hij bv. gaan stijgen en gaan draaien.

Een stijging gecombineerd met naar-beneden-draaien ziet er uit als een draaing met bv de neus als draaipunt.

duzz een vliegtuig kan uitstekend visueel draaien om een ander punt dan zijn zwaartepunt, maarrrr dan gaat het zwaartepunt dus omhoog of omlaag, duzzz dat betekend dat er een stukje stijgen of dalen aanwezig is. Haal je die eruit (aka je bekijkt het pure draaien) dan gaat het draaien tenslotte per definitie om het zwaartepunt.

robertooo

[robairo]

toch jammer dat ik deze niet in febr gezien heb, had arie bom er ook nog wat aan.