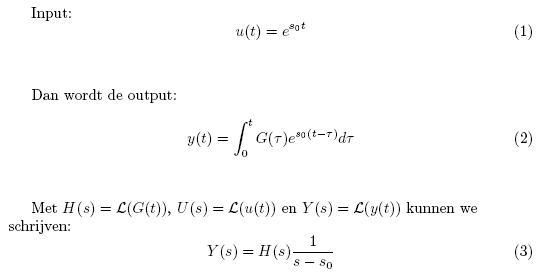Frequency response

[Arie Bombarie]

Goedendag,

Ik heb de volgende vraag:



Bij vergelijking (3) moet overigens nog staan: lim t-> oneindig.

Om deze nieuwe output (ook dit maal met lim t -> oneindig) te berekenen wordt in mijn boek simpelweg het imaginaire deel van vergelijking (3) genomen. Mijn vraag is waarom dit kan.

Alvast bedankt.

[Xenion]

Ik zie ook de link niet met vgl (3): (5) is toch gewoon opnieuw de input-output relatie als convolutie, met de input gedefinieerd in (4)?

(4) gebruikt deze eigenschap:

\(e^{i \omega t} = \cos{(\omega t)} + i\cdot \sin{(\omega t)}\)

[Arie Bombarie]

Klopt, uiteindelijk ben ik "op zoek" naar het volgende resultaat:

\(y_{2}(t)=|H(iw)|sin(wt+arg(H(iw)))\)

Mijn vraag is, hoe kom ik tot dit resultaat?

In het boek gaan ze aan de haal met het imaginaire gedeelte van vergelijking (3) om bovenstaande antwoord te verkrijgen. Een andere manier vind ik ook prima, maar ik zie niet hoe ik de convolutie-integraal kan uitwerken.

Het probleem voor mij is dat (5) niet direct om te zetten is naar het Laplace / Fourier domein, daar dit wel gemakkelijk met (1)-(2) kan.

[Xenion]

Goh, voor die convolutie zie ik zo direct niks, in het frequentiedomein kan je evt volgende redenering volgen.

Ik vind je formules vrij onduidelijk. Omega als frequentie van de sinus in het tijdsdomein, grote letter voor het impulsantwoord. :/

Het probleem voor mij is dat (5) niet direct om te zetten is naar het Laplace / Fourier domein, daar dit wel gemakkelijk met (1)-(2) kan.

De Fourier transformatie van een sinus is een dirac delta op de positieve en negatieve frequentie ervan (met een i ervoor, dus 90° fasedraaiing). Dat zal je normaal gezien verder in je boek nog wel tegenkomen, maar zie desnoods hier.

\(H(i\omega) = |H(i\omega)|*e^{i*arg(H(i\omega)\)

\(X(i\omega) = (\delta(-\omega_0)+\delta(+\omega_0))*e^{i\pi/2}\)

(Merk hier ook op dat ik

\(\omega\)

als variabele gebruik terwijl

\(\omega_0\)

de frequentie van de sinus is. Ik vind de notatie in je eerste post nogal verwarrend, zeker als je met transformaties gaat werken.)

Bij vermenigvuldigen van H met X bijft enkel de waarde bij de frequentie van de sinus over (pincet eigenschap):

\(Y(i\omega) = |H(\omega_0)|(\delta(-\omega_0)+\delta(+\omega_0))*e^{i(\pi/2 + arg(H(\omega_0))}\)

Het systeem draait dus de sinus in fase (exponentialen kan je in 1 schrijven en bij de sinus tellen) en verandert de amplitude. In het tijdsdomein vertaalt zich dat in de uitdrukking die je wil aantonen.

(Ervan uitgaande dat H symmetrisch is natuurlijk.)

[Arie Bombarie]

Bedankt voor je antwoord, ik ben bekend met de gegeven Fourier transformaties en de 'pincet eigenschap' (ik ken deze als de sifting property). Je afleiding is mij duidelijk.

Wat betreft de onduidelijke notaties, daarover ben ik het met je eens.

Laat ik een stap teruggaan, in de slides (en overigens ook in het boek) staat het volgende:



Ik heb al eerder een andere en begrijpbare afleiding gezien waarin hetzelfde resultaat wordt verkregen, het gaat mij er nu dan ook niet om hoe je dit resultaat kan verkrijgen, maar op de manier waarop dat hier gebeurd.

Wat ik uiterst frappant vind is de input:

\(u(t)=e^{st}\)

.

Hierin komt zowel de Laplace variable 's' als de tijdsvariabele 't' voor.

Ik dacht eerst dat ik in deze formule de 's' gewoon voor een bepaald complex nummer moet zien, net zoals dat je in x(t) = a*t de 'a' als een zekere constante voorstelt (dus géén variabele).

Ik zou dan eerder schrijven:

\(u(t)=e^{s_{0}t}\)

met

\(s_{0}\)

een zekere complexe waarde die we nu niet definiëren om het resultaat algemeen geldig te houden. Ik zou het dan op de volgende manier uitwerken:



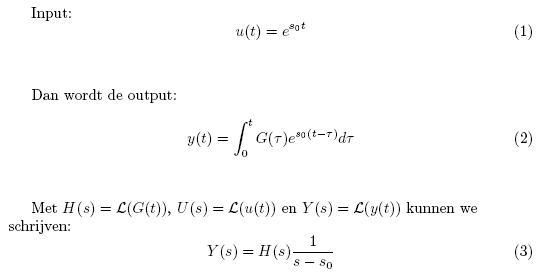
Dit resultaat is niet erg interessant.

In de uitwerking op de slides komt de 's' uit de input in de integraal voor, en dan krijgen we 'heel toevallig' een term die exact lijkt op de definitie van een Laplace integraal. Hier wordt de 's' uit de input dus gebruikt als Laplace / complexe variabele.

Zou je de input functie 'u' dan als functie van twee variabelen moeten zien; namelijk tijdsdomein variabele 't' en Laplace domein variabele 's'? Dit lijkt mij nogal vreemd...

[Xenion]

Zou je de input functie 'u' dan als functie van twee variabelen moeten zien; namelijk tijdsdomein variabele 't' en Laplace domein variabele 's'? Dit lijkt mij nogal vreemd...

Mja de notatie is inderdaad nogal verwarrend. Ook die redeneringen met die limieten vind ik maar louche. Ik denk dat je s best als een constante beschouwt zolang t nog niet 'weggeïntegreerd' is.

Wat betreft je originele vraag. Volgens mij mag je in vgl (5) die Im( ) operator over heel de integraal plaatsen, aangezien de systeemfunctie meestal zuiver reëel is. Daarmee kan je dan dezelfde limiet nemen als in (3) en de fasedraai door het systeem kan je dan mee in die complexe exponentiaal van de sinus nemen. Als je dan het imaginair deel neemt, dan komt die |H(iw)| er als constante gewoon uit en dan heb je volgens die eigenschap van exp(iwt) = cos(wt)+isin(wt) die sinus met fasedraai van de uitdrukking die je wil afleiden.