7 Eenhedenvergelijkingen
Wat je hierboven allemaal hebt geleerd kun je ook heel nuttig gebruiken om te controleren of berekeningen die je uitvoert in de natuurkunde of scheikunde ook werkelijk kloppen. Dat noemen we ook wel dimensie-analyse.
Soms zijn natuurkundeformules heel logisch:
\(v= \frac{s}{t}\)
Een afstand in meter gedeeld door een tijd in seconde geeft een snelheid in meter per seconde (m/s).
Je ziet dat aan allebei de kanten van de vergelijking óók de eenheden met elkaar kloppen.
\( {m/s} = \frac{m}{s}\)
\( m/s \)
kun je ook schrijven als
\( m\cdot s^{-1}\)
.
Die "m/s" noem je ook wel de dimensie van v (van de grootheid "snelheid". )
VALKUIL:
dit gaat natuurlijk alleen maar op zolang je overal in je formule SI-eenheden gebruikt.
Als je in
\(v= \frac{s}{t}\)
voor "v" de eenheid "km/h" gebruikt (of mach, of nog wat anders), dan klopt het niet meer:
\( {km/h} \neq \frac{m}{s}\)
.
Gelijk het bewijs dat je een snelheid in km/h niet kunt berekenen door een afstand in meters te delen door een tijd in seconden.......
 |
Maar vaak lijken natuurkundeformules wel toverspreuken: \( F = m\cdot a \)
Een massa in kilogram vermenigvuldigd met een versnelling in meter per secondekwadraat
geeft een kracht in newton. ???
Niet zo magisch als het lijkt hoor.
Het eerste wat je moet beseffen is dat er eigenlijk maar 7 grondeenheden bestaan:
meter (m), kilogram (kg), seconde (s), ampère (A), kelvin (K), candela (cd) en mol (mol)
|
(zie ook hoofdstuk 2 van de
microcursus Grootheden, eenheden, voorvoegsels en symbolen):
In grondeenheden uitgedrukt is de eenheid van kracht gewoon de eenheid van massa (kg) vermenigvuldigd met de eenheid van versnelling (m/s²):
een kilogrammeterpersecondekwadraat. (kg·m/s², of ook wel kg·m·s-2)
Nou is dat nogal een mond vol (en bovendien hebben we nog allerlei grote natuurkundigen uit het verleden die we moeten eren !! ).
Daarom spreken we af dat we die
kg·m/s² gewoon een newton (N) noemen. In elke taal heb je ook meerdere woorden die eigenlijk hetzelfde betekenen (synoniemen), toch?
\( F = m\cdot a\)
lijkt dus alleen een toverspreuk omdat we die eenheid van kracht een eigen naam hebben gegeven. Voor de rest klopt de vergelijking, ook in eenheden, als een zwerende vinger.
Alle SI-eenheden, de newton, de ohm, de coulomb, de volt, de joule, de tesla, de farad, de hertz, de bequerel, de henry en ga zo maar door, állemaal zijn ze te schrijven in grondeenheden.
En in élke formule, als je in de plaats van de grootheden de bijbehorende eenheden invult, blijft de formule kloppen.
Nog een voorbeeld:
\(P=\frac{E}{t}\)
. Deel een energie in joule door een tijd in seconde, en de uitkomst is een vermogen in watt (W).
maar ook:
\(P=U\cdot I\)
, vermenigvuldig een spanning in volt met een stroomsterkte in ampère en de uitkomst is óók een vermogen in watt. ????
Kijken we eens even naar een paar definities:
Een coulomb is de lading van een hoeveelheid elektronen. Je batterij geeft energie aan die elektronen waardoor ze door de draad gaan bewegen. Als een batterij 1 joule energie aan 1 coulomb lading geeft heb je precies 1 volt. Dus een volt is een joule per coulomb.
\( volt = \frac{joule}{coulomb}\)
Een coulomb is de lading van een hoeveelheid elektronen. Als er op een punt in je stroomkring elke seconde een coulomb lading voorbij komt heb je daar een stroomsterkte van precies 1 ampère. Dus een ampère is een coulomb per seconde.
 Vul nou in
Vul nou in  eens de eenheden in, schrijf die eenheden anders en werk het uit:
eens de eenheden in, schrijf die eenheden anders en werk het uit:

Nou ook in de andere,
\(P=\frac{E}{t}\)
:
\((P=)watt=\frac{joule}{seconde}=\frac{J}{s}\)
Zo zie je, als je het ver genoeg doorvertaalt staat er in allebei de formules dus eigenlijk gewoon hetzelfde. Die watt is niks anders dan een andere naam voor J/s (vernoemd naar
James Watt)
Nog een paar voorbeelden:
In elke natuur- of scheikundeformule staan grootheden, bijvoorbeeld die
\(R = \frac{\rho \times l}{A}\)
Misschien weet je dat de eenheid van soortelijke weerstand :rho: de Ωm (ohmmeter) is.
Gek ding, zo'n Ωm. Hoe komt dat?
| \(R = \frac{\rho \times l}{A}\) |
| Maar vul nou in de plaats van elke grootheid eens de bijbehorende eenheid in: | \(\Omega = \frac{(eenheid \ van \ \rho) \times m}{m^2}\) |
| m/m² = 1/m | \(\Omega = \frac{(eenheid \ van \ \rho) \times 1}{m}\) |
| Dan: beide zijden vermenigvuldigen met m: | \(\Omega \times m= \frac{(eenheid \ van \ \rho)\times m}{m}\) |
| Dan nog even oppoetsen: | \(\Omega m= (eenheid \ van \ \rho)\) |
Stoichiometrie in de scheikunde is ook zo'n heet hangijzer met stapels formuletjes die geen zinnig mens kan onthouden.
500 mL oplossing HCl (molmassa 36,5 g) met een molariteit van 0,1 M , hoeveel gram HCl zit daar in?
\(m=\frac{M}{\frac{mm}{V}}\)
??
\(m= V\times mm\times M\)
??
\( m = V\times \frac{mm}{M}\)
??
Nou, probeer eens met eenheden:
je moet een antwoord in gram hebben . Molariteit heeft de eenheid mol/L , molmassa heeft de eenheid g/mol.
Proberen dan maar:
\(m=\frac{M}{\frac{mm}{V}}\)
??
\( g = \frac{\frac{mol}{L}}{\frac{\frac{g}{mol}}{L}}\)
.... ??Daar komt nooit iets van terecht....
\({....} = \frac{mol^2}{g\times L^2}\)

nog maar eens proberen:
\(m= V\times mm\times M\)
??
\( g =L \times {\frac{mol}{L}}\times{\frac{g}{mol}} = \frac {L \times g \times mol}{mol\times L} \)
mol/mol = 1, L/L = 1, nou klopt 'ie wel.
\( g = \frac {1 \times g \times 1}{1\times 1} = g \)
Zo kun je dus altijd vrij vlot aan een eenhedenvergelijking zien of een formule die je wil gaan gebruiken ook inderdaad klopt.

\(800N \times 2 m = 400N \times 1,8 m + 400 N \times 2,2 m\)
 .
.  ?
? de I te halen?
de I te halen?







 van beide zijden 3 aftrekken:
van beide zijden 3 aftrekken: 


 betekent eigenlijk
betekent eigenlijk 

















 maar ook
maar ook  )
) beide zijden delen door 2:
beide zijden delen door 2: 


 zou je kunnen lezen als
zou je kunnen lezen als  en is hetzelfde als
en is hetzelfde als 



 . Hierboven zag je al hoe je dat nuttig kunt gebruiken.
. Hierboven zag je al hoe je dat nuttig kunt gebruiken. . Ook dat zag je hierboven al. ( zelfs
. Ook dat zag je hierboven al. ( zelfs  )
) niet klopt.
niet klopt. . Niet doen dus.
. Niet doen dus. dan wordt met die "3" bedoeld "+3" . Moet de 3 weg, dan zul je dus de bewerking "-3" moeten toepassen.
dan wordt met die "3" bedoeld "+3" . Moet de 3 weg, dan zul je dus de bewerking "-3" moeten toepassen. , en de 3 moet weg, moet je óók door 3 delen, al staat er geen "x" teken vóór de 3.
, en de 3 moet weg, moet je óók door 3 delen, al staat er geen "x" teken vóór de 3. precies hetzelfde betekent.
precies hetzelfde betekent. , elk van de leden tussen haakjes zetten:
, elk van de leden tussen haakjes zetten: , beide leden delen door
, beide leden delen door  :
:
 :
: , we vermenigvuldigen beide leden met -1 :
, we vermenigvuldigen beide leden met -1 :


 , reken maar na:
, reken maar na: 
 reken maar na:
reken maar na: 
 , dan geldt ook
, dan geldt ook  ,
, , dan geldt ook
, dan geldt ook 

 ?
? schrijven als breuk:
schrijven als breuk: 

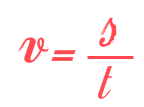
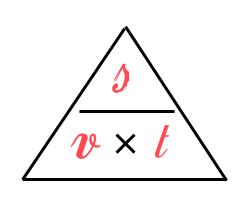


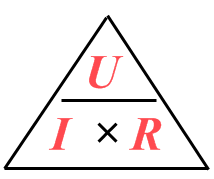
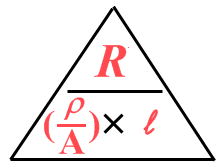





 [/td][/tr]
[/td][/tr]