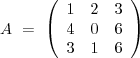Tensoren begrijpen

[mathfreak]

Begrijp je wel dat een dyade als een matrixproduct van de eerste vector als kolomvector en de tweede vector als kolomvector kan worden opgevat? Dat is namelijk wat er in die definitie op Wikipedia staat.

[Th.B]

Je bedoelt: de tweede vector als rijvector.
Eigenlijk doe je in quantummechanica hetzelfde als je de Dirac-notatie gaat gebruiken. Daar is de vectorruimte bijvoorbeeld L₂ over de complexe getallen en is de dyad [ψ> <ψ] een operator die de projectie op ψ geeft. De 'ket' is het element uit de vectorruimte zelf, en de 'bra' komt uit de duale vectorruimte.

[Professor Puntje]

Ik vind die matrix-definitie logisch ondeugdelijk. Zo'n matrix bevat getallen, en geen producten van getallen. Men kan in een matrix wel producten schrijven, maar dat betekent dan dat de betreffende elementen van de matrix de uitkomst van die producten als waarde hebben. De onderstaande matrices A en B zijn identiek:

\( A \,\, = \,\, \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 0 & 6 \\ 3 & 1 & 6 \end{array} \right) \)

\( B \,\, = \,\, \left( \begin{array}{ccc} 1.1 & 1.2 & 6.1/2 \\ 2.2 & 0.9 & 3.2 \\ 3.1 & 1.1 & -3.-2 \end{array} \right) \)

Een definitie als lineaire afbeelding van een n-dimensionale euclidische ruimte in een n-dimensional euclidische ruimte is logisch zuiver, want iets is wel of niet een dergelijke afbeelding. De wijze waarop het betreffende wiskundige object (in dit geval een afbeelding) concreet wordt omschreven is irrelevant.

Dat het er in de wiskunde regelmatig anders aan toe gaat is voor mij steeds een grote hindernis: ik moet dan eerst voordat ik verder kan zelf op zoek naar logisch zuivere definities die wel in de haak zijn.

[anusthesist]

Het gaat om deze video's:

 
https://www.youtube.com/watch?v=hR7fWF_qBZI&feature=relmfu

 
https://www.youtube.com/watch?v=ttMI0dmmkrE&feature=relmfu

 
https://www.youtube.com/watch?v=WtPtxz3ef8U&feature=relmfu

Weet niet meer welke, maar in 1 van deze GRT lectures gaag hij vrij diep op tensoren in en bij de basis begint van vectors en scalars etc.

[mathfreak]

De onderstaande matrices A en B zijn identiek:



 



 

 

Ze zijn alleen identiek wat het aantal rijen en kolommen betreft. We noemen 2 matrices identiek als ze naast hetzelfde aantal rijen en kolommen ook dezelfde elementen bevatten, dus in die zin zijn de door jou genoemde matrices niet identiek.
 

 
Dat het er in de wiskunde regelmatig anders aan toe gaat is voor mij steeds een grote hindernis:

 
Wat bedoel je precies met dat het er in de wiskunde regelmatig anders aan toe gaat?
 
 

 ik moet dan eerst voordat ik verder kan zelf op zoek naar logisch zuivere definities die wel in de haak zijn.
 

Met de wiskundige definities zelf is niets mis. Ze zijn wel degelijk logisch zuiver, maar als je niet weet hoe je ze moet interpreteren wil dat niet zeggen dat ze niet in de haak zijn.

[Professor Puntje]

Ze zijn alleen identiek wat het aantal rijen en kolommen betreft. We noemen 2 matrices identiek als ze naast hetzelfde aantal rijen en kolommen ook dezelfde elementen bevatten, dus in die zin zijn de door jou genoemde matrices niet identiek.

 
Tenzij ik een domme rekenfout heb gemaakt, zijn A en B - volgens mij - wel identiek. Laat ik nog een eenvoudiger voorbeeld geven:
 

\( A \,\, = \,\, \left( \begin{array}{cc} 1 & 2 \\ 4 & 1+3 \end{array} \right) \)

\( B \,\, = \,\, \left( \begin{array}{cc} 1 & 2 \\ 4 & 2+2 \end{array} \right) \)

 
Vragen:
 
Zijn A en B identiek?
 
Zijn A en B niet identiek?
 
Zijn A en B gelijk?
 
Zijn A en B ongelijk?
 
 

[mathfreak]

 
Tenzij ik een domme rekenfout heb gemaakt, zijn A en B - volgens mij - wel identiek. Laat ik nog een eenvoudiger voorbeeld geven:

Ze zijn bij nader inzien inderdaad identiek, mits je als maalteken de gecentreerde punt gebruikt. De LaTeX-code voor dit teken is \cdot.

[Professor Puntje]

Mogelijk zie je nu ook wat mijn bezwaar tegen de Wikipedia-definitie is?
 
Ik heb vandaag weer heel veel via internet nagezocht, en de meest logische definitie die ik ben tegengekomen is degene die ik al eerder in berichtje #14 heb geplaatst. Daar ga ik dus mee verder. Met die definitie vind je (bij gekozen basisvectoren) ook een met de afbeelding corresponderende matrix dus ik heb goede hoop dat de concrete theorie zo hetzelfde blijft. 

[anusthesist]

Gevonden. Vanaf 52:20:

[Professor Puntje]

@ anusthesist
 
Dank voor de nadere aanwijzing waar de tensoren behandeld worden. Ik heb alleen het stukje gekeken waar de tensoren gedefinieerd worden. Dat gaat in de video op de manier waarop fysici dan meestal doen. Ook heeft Susskind gezien zijn antwoorden op de vragen blijkbaar geen boodschap aan wiskundige subtiliteiten. Onder fysici komt ook dat wel meer voor, en vanuit natuurkundig perspectief zijn wiskundige subtiliteiten ook meestal irrelevant. Maar ik wil zelf wat dieper graven.

[Professor Puntje]

dyadic 658 keer bekeken

 
Dit is een bladzijde uit Louis Brands Vector and tensor analysis. We zien dat een dyade kan worden opgevat als een specifieke representatie in operatorvorm van een lineaire vectorfunctie. Gelijkheden van dyades kunnen bij deze manier van definiëren worden opgevat als gelijkheden van de corresponderende lineaire vectorfuncties. Op die manier verdwijnt de akelige willekeurigheid (afgezien van de definities van bewerkingen) uit de rekenregels voor dyades, de identiteiten uit de theorie moeten nu immers opgaan voor de lineaire vectorfuncties waar de dyades naar verwijzen. Dat maakt dat de theorie - ook voor mij - controleerbaar wordt. Er wordt dan iets beweerd over bestaande wiskundige objecten (de lineaire vectorfuncties) dat waar of onwaar kan zijn. Dat is het type wiskunde dat mij aanspreekt.

[Professor Puntje]

Ik stop met de teksten van Joseph C. Kolecki waar ik in berichtjes #1 en #4 naar gelinkt heb. De daarin gehanteerde aanpak spreekt mij bij nader inzien onvoldoende aan.

[Professor Puntje]

In Dictaat en vraagstukken bij Tensorrekening en Differentiaalmeetkunde van J. de Graaf wordt in de paragraaf '1.9 Een wiskundige interpretatie van het ’ingenieurs tensor begrip’ ' een definitie van tensoren gegeven die op het eerste gezicht zowel praktisch bruikbaar is als wiskundig correct. Het dictaat is op internet te vinden:
 
http://www.win.tue.nl/~degraaf/2F800/TENSOR.pdf

[Professor Puntje]

Het kwartje is gevallen: ik begrijp de "’ingenieursdefinitie" van tensoren. Het grondig doorwerken van het dictaat (en maken van de opgaven) is werk voor volgend jaar.