Deeltjes of geen deeltjes ?

[wnvl1]

Ik ben in België naar school geweest, daarom dat ik mts niet juist kan inschatten. Maar ik vermoed dat het overeenkomt met technisch onderwijs op het niveau van het middelbaar dus tussen 12 en 18 jaar. In België ga je in het geval van de richting industrieel wetenschappen een beetje te kort komen, maar het kan misschien nog net. In geval van een mechanica technische richting ga je in België redelijk wat te kort komen.

Ik denk dat in Nederland een vwo richting gericht op wiskunde misschien volstaat voor dit quantum mechanica boek?

[Gps]

In Nederland is het lagere school, tot 12 jaar
Dan LTS of MAVO 12 - 16 jaar
Daarna heb je MTS of HAVO.
Daarna HTS of Universiteit.

Hoe ik VWO ( duurt 6 jaar ) in dit lijstje moet zetten weet ik niet zeker.
Eventueel moeten mensen me maar corrigeren, maar ik dacht:
Lagere school, VWO, dan universiteit (of HTS)

Vooropleiding voor MTS is dus LTS of MAVO

Meer concreet, ik heb dus geen integraal berekeningen gehad, maar wel Booleaanse algebra.
Y= a + niet b

Had ik op de MTS wiskunde als examen vak gekozen, dan had ik wel integraal berekeningen gehad en ik vermoed ook complexe nummers.

Op de MTS krijg je ook sterkte berekeningen. Mb = Wb x Sigma b
Goochelen met formules en het Griekse alfabet, doe je op de MTS dus ook al.

Zo is er ook het traagheidsmoment, mm^4. (met de uitleg dat je niet moet proberen om je daar bij wat bij voor te stellen)

Shut up and compute

[Gps]

Quantum mechanics demystified.

Het voordeel van de demystified reeks is dat alle tussenliggende berekeningen geincludeerd zijn in het boek. Voorwaarde blijft wel dat je de wiskunde van het secundair en liefst het eerste jaar hoger onderwijs perfect beheerst, anders heeft het geen nut om aan het boek te beginnen.

Ik heb in dezelfde reeks ook quantum field theory demystified gekocht, maar die lukt mij niet om te doorgronden, te lastig.

Ik ga opzoek naar dat boek, de titels klinken wel bekent.

Ik denk dat kwantum mechanica moeilijk te begrijpen is, omdat de mensen die het ons uitleggen ook niet echt begrijpen hoe het in detail werkt. (double slit als voorbeeld)

Leuke uitspraak van Einstein, de maan is er ook als ik er niet naar kijk.

Hoewel het lastig en gevaarlijk is om je intuïtie te gebruiken bij dit onderwerp, de kwantum veld theorie voelt bij mij erg goed.

Verder helpt een goede leraar ook. Leonard Susskind met alle respect vind ik geen geweldige leraar.
Dat kunnen Feyman, Neal de degrasse Tyson en Brian Green beter.
Iets heel moeilijks simpel laten lijken.

Met Susskind heb ik het wel een beetje gehad. Legt tie uit dat je niet sneller kan reizen dan het licht, en voegt er aan toe, kom niet aan met die onzin, over een trein in een trein.

Vooral dat hij niet uitlegt waarom dat onzin is, zit me nog steeds dwars.

Voor wie dat trein voorbeeld niet kent.
Men neme een trein en laten die met 0,75% van de licht snelheid rijden, vervolgens starten we in die trein een tweede trein, die we laten rijden met een snelheid van 0,75 % van de licht snelheid.

Voor een persoon buiten beide treinen gaat die tweede trein dan sneller als het licht.
Erg jammer dat hij niet uitlegt, waarom dat onzin is.

[wnvl1]

Verder helpt een goede leraar ook. Leonard Susskind met alle respect vind ik geen geweldige leraar.
Dat kunnen Feyman, Neal de degrasse Tyson en Brian Green beter.
Iets heel moeilijks simpel laten lijken.

Sean Caroll mag je ook toevoegen aan dat lijstje van top wetenschapscommunicators, vind ik.
David Tong is wat jonger, maar is ook een briljante combinatie van wetenschapper en entertainer.

De boeken voor het grote publiek van Leonard Susskind zijn wel goed. Leonard Susskind heeft ook wel goede dingen op Youtube staan, maar hij is geen communicator van het niveau van de anderen in jouw lijstje. Ik heb daarmee niet gezegd dat hij niet goed is. Degenen die je aanhaalt zijn dan ook absolute wereldtop op het vlak van communicatie.

Voor de Demystified reeks is een degelijke achtergrond in integraalrekening wel nodig. Ook complexe getallen zijn nodig voor QM. Ik begrijp dat je die niet hebt voorlopig. Aan booleaanse algebra ga je in deze context niet veel hebben. Voorlopig gaat het dan nog niet lukken om te starten in deze boeken, denk ik.

Integraalrekening zelf studeren tot een niveau dat je het vlot kan, kost vermoedelijk wel twee jaar. Het is wel noodzakelijk, anders ga je het gefrustreerd opgeven. Mits deze wiskunde is QM best wel te doen. Het is bvb veel gemakkelijker dan ART om een zeker niveau te bereiken. De interpretaties blijven wel mysterieus, dat staat los van de wiskunde.

[Gps]

Het is jammer dat ik me wiskundeboek van de mts weg gegooid heb.
Dat boek had een hoofdstuk, complexe getallen en ik geloof ook integraal rekenen, maar met het huidige internet moet dat verder geen probleem zijn.

De wortel uit -j, here I come.

[wnvl1]

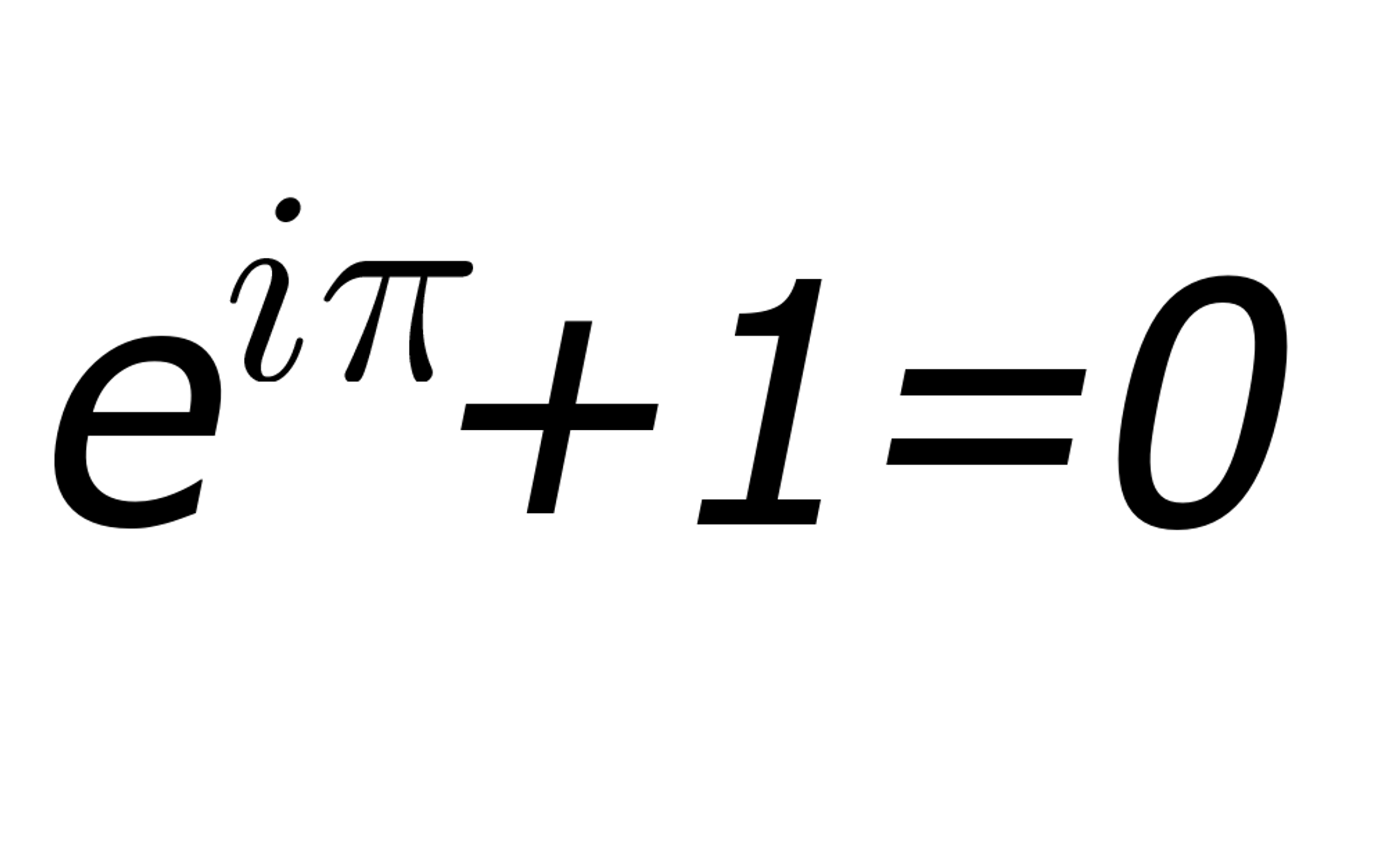
De mooiste vergelijking die er bestaat

[flappelap]

Van Wikipedia verder:

"A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states:

\({\displaystyle \rho _{\mathrm {pure} }=|\psi \rangle \langle \psi |}\)

\({\displaystyle \rho _{\mathrm {mixed} }=\sum p_{i}|\psi _{i}\rangle \langle \psi _{i}|,}\) "

Ik vat dat op als een combinatie van kwantumtoestanden die gezamenlijk weer één kwantum toestand beschrijven.

Dus, hoe zie jij dat dan?

Ja, dat zie ik ook zo. Een kwantumtoestand is een vector in de Hilbertruimte, dus een lineaire combinatie van kwantumtoestanden levert ook weer een vector op. Vaak neem je als basisvectoren van deze ruimte de eigenvectoren van de desbetreffende operator (grootheid) waar je in geïnteresseerd bent.

[flappelap]

In een poging om bovenstaande "discussie" te volgen, kwam ik hier terecht.
https://en.wikipedia.org/wiki/Quantum_state

A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers

Iets met dat ik de woorden wel begrijp, maar de zin niet echt.

Misschien mis ik iets, maar dit geldt niet alleen voor pure toestanden, maar voor elke toestand (golffunctie).

Naief zou je zeggen dat een kwantumtoestand gerepresenteerd wordt met een golffunctie \(\psi(t,x)\), en de bijbehorende kansverdeling met \(\psi^* \psi\). Maar er is geen 1-op-1 relatie tussen toestand en golffunctie. Want als je een nieuwe golffunctie \(\psi' \equiv e^{i\theta(t,x)}\psi \) definiëert voor een willekeurige functie \(\theta(t,x)\) , dan geldt er

\(\psi^{'*} \psi' = \psi^* \psi\)

Oftewel: \(\psi\) en \(\psi' = e^{i\theta}\psi\) geven dezelfde kansverdeling en dus experimentele uitkomsten. Zo'n equivalentieklasse aan golffuncties noemen we een "ray", oftewel alle golffuncties \(\psi\) met een willekeurige fasefactor vermenigvuldigd. Elk element uit zo'n equivalentieklasse of "ray" representeert dezelfde kwantumtoestand.

Dat lijkt een detail, maar blijkt uiteindelijk wel belangrijk te zijn. Je weet bijvoorbeeld dat in de klassieke mechanica inertiaalwaarnemers (waarnemers die onderling met constante snelheid bewegen en dus dezelfde experimentele uitkomsten vinden) verbonden zijn via de coordinatentransformatie ("boost")

\(x' = x + vt \)

De tweede wet van Newton verandert hierdoor niet. De Schrödingervergelijking moet net zo invariant blijven onder een dergelijke "boost", anders zouden verschillende inertiaalwaarnemers verschillende experimentele uitkomsten vinden (wat in theorie zou kunnen, maar waarvoor geen enkele empirische reden voor is). En dan blijkt de naieve regel dat de golffunctie invariant ("scalair") is onder zo'n boost,

\(\psi'(x') = \psi(x) \)

niet op te gaan; in plaats daarvan blijkt te gelden dat

\(\psi'(t',x') = e^{i\theta(t,x)}\psi(t,x) \)

voor een zekere functie \(\theta(t,x)\) die je expliciet kunt afleiden door de hele zaak in de Schrodingervergelijking te stoppen en een coordinatentransformatie uit te voeren (maar hier verder niet zo boeiend is). Dit heeft weer te maken met technische details omtrent de golffunctie als representatie onder de onderliggende symmetriegroep. Het klassieke artikel hieromtrent is

V. Bargmann, On Unitary Ray Representations of Continuous Groups. Ann. of Math., 59 (1954)

Het feit dat een kwantumtoestand gerepresenteerd wordt met zo'n "ray" is dus cruciaal om de Schrodingervergelijking invariant te houden onder "boosts".

Nou ja, ik weet niet wat je hier allemaal uit kunt halen, maar voor een indruk

[flappelap]

Quantum mechanics demystified.

Het voordeel van de demystified reeks is dat alle tussenliggende berekeningen geincludeerd zijn in het boek. Voorwaarde blijft wel dat je de wiskunde van het secundair en liefst het eerste jaar hoger onderwijs perfect beheerst, anders heeft het geen nut om aan het boek te beginnen.

Ik heb in dezelfde reeks ook quantum field theory demystified gekocht, maar die lukt mij niet om te doorgronden, te lastig.

QFT is ook een notoir lastig onderdeel van de natuurkunde, omdat je er (1) nogal wat gevorderde wiskundige technieken voor nodig hebt (contourintegratie, functionaalanalyse, groepen- en representatietheorie, etc) en (2) omdat tekstboeken vaak vrij losjes de wiskundige onderbouwing geven omdat je anders al 500 bladzijden bezig bent om een simpel deeltje te beschrijven De formele wiskundige onderbouwing, die nog steeds niet helemaal is dichtgetimmerd, staat bekend als "algebraic quantum field theory", maar is zo gortdroog en taai dat je wel een sadomasochist moet zijn om dat voor de lol door te nemen.

Ik ben zelf ooit tevergeefs op zoek geweest naar een boek waarin deze wiskundige technieken en redenaties aannemelijk worden behandeld, maar dat bleek dus tevergeefs. Wat wel helpt: neem een tekstboek, en ga naar een forum als physicsforums om je vragen te stellen bij alles wat je tegenkomt. Uiteindelijk kan ik zeggen dat ik een prima begrip heb van QFT, maar daar ging heel (heel!) erg veel tijd in zitten, en ondertussen heb ik iets van 10 tekstboeken hier thuisliggen.

[flappelap]

Misschien kunnen we voor de aardigheid de rollen eens omdraaien.

1 Stel dat we de twee smalle spleten naar het stilstaande deeltje laten bewegen.
Ziet het deeltje die twee smalle spleten dan als een golfbeweging?
Daarbij bevinden we ons zelf in het referentiekader van het deeltje.

2 Als een geladen deeltje door een dubbele spleet gaat, gaat dan een deel van zijn electrische veld niet door de tweede spleet, of wordt het veld dan vervormd?
En wat heeft die vervorming voor effect op de weg van het deeltje, als het niet precies midden door de spleet vliegt, of als een deel van het veld door de andere spleet gaat?

1 De experimentele resultaten zullen dus hetzelfde zijn; in feite "boost" je jezelf naar het ruststelsel van het deeltje (zie mijn eerdere post). Je vraag "Ziet het deeltje die twee smalle spleten dan als een golfbeweging?" snap ik niet; nee, in feite beschrijf je in zo'n opzet de spleten niet met een golffunctie, maar behandel je dit als een klassiek voorwerp.

2 Dat is een goede vraag. Wat exact het verschil in wisselwerking is tussen spleten en deeltje, en spleten en geladen deeltje, dat hangt af van hoe gedetailleerd je die wisselwerking beschrijft. In feite zou het elektrisch veld van het deeltje het materiaal van de spleten polariseren, wat weer een terugkoppeling heeft op het deeltje. In praktische berekeningen zul je denk ik aannemen dat dit soort wisselwerkingen er niet zijn en de opstelling ondoordringbaar is voor het elektrische veld van het deeltje.

[flappelap]

Quantum mechanics demystified.

Het voordeel van de demystified reeks is dat alle tussenliggende berekeningen geincludeerd zijn in het boek. Voorwaarde blijft wel dat je de wiskunde van het secundair en liefst het eerste jaar hoger onderwijs perfect beheerst, anders heeft het geen nut om aan het boek te beginnen.

Ik heb in dezelfde reeks ook quantum field theory demystified gekocht, maar die lukt mij niet om te doorgronden, te lastig.

Ik ga opzoek naar dat boek, de titels klinken wel bekent.

Ik denk dat kwantum mechanica moeilijk te begrijpen is, omdat de mensen die het ons uitleggen ook niet echt begrijpen hoe het in detail werkt. (double slit als voorbeeld)

Leuke uitspraak van Einstein, de maan is er ook als ik er niet naar kijk.

Hoewel het lastig en gevaarlijk is om je intuïtie te gebruiken bij dit onderwerp, de kwantum veld theorie voelt bij mij erg goed.

Verder helpt een goede leraar ook. Leonard Susskind met alle respect vind ik geen geweldige leraar.
Dat kunnen Feyman, Neal de degrasse Tyson en Brian Green beter.
Iets heel moeilijks simpel laten lijken.

Met Susskind heb ik het wel een beetje gehad. Legt tie uit dat je niet sneller kan reizen dan het licht, en voegt er aan toe, kom niet aan met die onzin, over een trein in een trein.

Vooral dat hij niet uitlegt waarom dat onzin is, zit me nog steeds dwars.

Voor wie dat trein voorbeeld niet kent.
Men neme een trein en laten die met 75% van de licht snelheid rijden, vervolgens starten we in die trein een tweede trein, die we laten rijden met een snelheid van 75 % van de licht snelheid.

Voor een persoon buiten beide treinen gaat die tweede trein dan sneller als het licht.
Erg jammer dat hij niet uitlegt, waarom dat onzin is.

Als je een mooi overzicht wilt van interpretaties en filosofie rondom de QM, dan kan ik het boek "foundations of QM" van Travis Norsen erg aanraden. Maar daar heb je wel een degelijke kennis van QM voor nodig. Daarin wordt ook Einsteins uitspraak omtrent de maan en zijn opvatting van "lokaal realisme" uiteengezet.

Omtrent die treinen: je kunt in de relativiteitstheorie niet zomaar snelheden meer bij elkaar optellen. De manier om snelheden wel op te tellen volgt uit de definitie van (coördinaten)snelheid, en de Lorentztransformaties. Voor een persoon buiten beide treinen gaat de tweede trein dan met 96% van de lichtsnelheid.

Dat lijkt vreemd, maar in de relativiteitstheorie zijn ruimtelijke snelheden geen vectoren meer, omdat je in de ruimteTIJD werkt. Alleen vectoren in de ruimtetijd kun je simpel optellen. Zie

https://en.wikipedia.org/wiki/Velocity-addition_formula

[Gps]

Met Susskind heb ik het wel een beetje gehad. Legt tie uit dat je niet sneller kan reizen dan het licht, en voegt er aan toe, kom niet aan met die onzin, over een trein in een trein.

Vooral dat hij niet uitlegt waarom dat onzin is, zit me nog steeds dwars.

Voor wie dat trein voorbeeld niet kent.
Men neme een trein en laten die met 75% van de licht snelheid rijden, vervolgens starten we in die trein een tweede trein, die we laten rijden met een snelheid van 75 % van de licht snelheid.

Voor een persoon buiten beide treinen gaat die tweede trein dan sneller als het licht.
Erg jammer dat hij niet uitlegt, waarom dat onzin is.

Als je een mooi overzicht wilt van interpretaties en filosofie rondom de QM, dan kan ik het boek "foundations of QM" van Travis Norsen erg aanraden. Maar daar heb je wel een degelijke kennis van QM voor nodig. Daarin wordt ook Einsteins uitspraak omtrent de maan en zijn opvatting van "lokaal realisme" uiteengezet.

Omtrent die treinen: je kunt in de relativiteitstheorie niet zomaar snelheden meer bij elkaar optellen. De manier om snelheden wel op te tellen volgt uit de definitie van (coördinaten)snelheid, en de Lorentztransformaties. Voor een persoon buiten beide treinen gaat de tweede trein dan met 96% van de lichtsnelheid.

Dat lijkt vreemd, maar in de relativiteitstheorie zijn ruimtelijke snelheden geen vectoren meer, omdat je in de ruimteTIJD werkt. Alleen vectoren in de ruimtetijd kun je simpel optellen. Zie

https://en.wikipedia.org/wiki/Velocity-addition_formula

Dank je wel, en waarom ik dit zo moeilijk vind om te begrijpen, is omdat als ik dit met een brommer in een trien doe, ik de snelheden wel mag optellen.

Trein 80 km/u , brommer 40 km/u, voor iemand buiten de trein gaat de brommer met 120 voorbij. Of klopt dat ook niet?

Ik heb in ieder geval het goede forum gevonden om dit soort vragen te stellen.

[Xilvo]

Opmerking moderator

Het is niet nodig steeds volledige berichten te quoten.
Quote alleen het stukje waarop waarop je wil reageren. Zo blijven topics leesbaar.

[Xilvo]

...en waarom ik dit zo moeilijk vind om te begrijpen, is omdat als ik dit met een brommer in een trien doe, ik de snelheden wel mag optellen.

Trein 80 km/u , brommer 40 km/u, voor iemand buiten de trein gaat de brommer met 120 voorbij. Of klopt dat ook niet?

Het is lastig te begrijpen omdat het begrip gebaseerd is op wat je dagelijks ziet.
Als de lichtsnelheid 25 km/h zou zijn dan zag je dagelijks dat je snelheden niet mag optellen en zou je niet beter weten.

Nee, ook die brommer krijgt geen snelheid van 120 km/h. Al is het verschil zo ontzettend klein dat het niet meetbaar is; iets van 3.10^-13 km/h.

[Gps]

Dank je wel, nu begin ik het al een stuk logischer te vinden.

Dit doet me denken aan een aflevering van PBS, daar heeft hij het er over dat veel formules die we gebruiken niet exact zijn, maar dat we dit verschil in het dagelijks leven niet merken.

De brommer in de trein is daar dus een voorbeeld van.