E=mc²

[Professor Puntje]

@ always
 
De afleiding die in de link staat geldt alleen voor kogels (en andere stoffelijke voorwerpen) die zich voortbewegen met snelheden die véél kleiner zijn dan de lichtsnelheid. Voor voorwerpen of deeltjes die zich voortbewegen met relativistische snelheden (dus de lichtsnelheid of een snelheid in de buurt daarvan) gaat de klassieke mechanica niet meer op en moet je de relativiteitstheorie gebruiken.

[Moab]

En nu mijn vraag ,
hoe bepaal je massa in kilogram ?
met dezelfde weegmethode is je massa kleiner op de maan
is je kinetische energie dan ook kleiner ?

[Professor Puntje]

Door wegen bepaal je het gewicht, niet de massa.

[Marko]

En nu mijn vraag ,
hoe bepaal je massa in kilogram ?
met dezelfde weegmethode is je massa kleiner op de maan
is je kinetische energie dan ook kleiner ?

 
Je hebt in die zin gelijk dat als je een weegschaal gebruikt, deze op de maan een ander getal zou aangeven. Maar deze weegschaal geeft niet de massa aan maar het gewicht. De massa blijft gelijk, en de kinetische energie dus ook.
 
Ook op de maan kun je overigens prima de massa bepalen. In algemene zin komt meten neer op vergelijken met een standaard. Het is dus een kwestie van een standaard hebben, en op een goede manier vergelijken. Dat kan op verschillende manieren, en bij wegen is dat eigenlijk heel makkelijk, met een balans. Dan leg je je onbekende massa in de ene schaal en gebruik je precies zoveel bekende massa's totdat de boel in balans is - enfin, je zult weten hoe een balans werkt. Maar waar het eigenlijk om gaat is wat men dan fysisch aan het doen is: zoals aangegeven, op een slimme manier vergelijken met bekende standaarden. Als je die standaarden meeneemt naar de maan kun je ook daar prima massa's bepalen.

[always]

 Voor voorwerpen of deeltjes die zich voortbewegen met relativistische snelheden (dus de lichtsnelheid of een snelheid in de buurt daarvan) gaat de klassieke mechanica niet meer op en moet je de relativiteitstheorie gebruiken. E=mc² en de uitdrukking E_kin=1/2mv² 
 
STel je hebt een massa van 2 kg. Met snelheid van 0,5c.
Ekin=1*22.500.000.000m/s=22,5.10⁹ kgm²s²
E=2*22.500.000.000m/s=45.10⁹ kgm²s²
 
En ook al zijn c en v verschillende grootheden je kunt ze wel in elkaar omzetten, toch? Als iets 200km/u (=v) gaat gaat deze dus (v=) 0,000054c. Met de E_kin kom ik dan op een waarde uit die altijd die twee maal zo klein is als met E.
Waarom is dat dan precies 2. Maw wat zorgt ervoor dat de relativistische 'methode' altijd een tweemaal hogere waarde lijkt te geven?

[mathfreak]

Probeer de klassiek-mechanische uitdrukking voor kinetische energie en de relativistische massa-energierelatie eens als 2 afzonderlijke situaties te beschouwen. De klassiek-mechanische uitdrukking voor kinetische energie gebruik je uitsluitend voor de alledaags voorkomende snelheden. Voor snelheden in de buurt van de lichtsnelheid is de totale energie gelijk aan

\(\frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}\)

Hierbij is m₀ de rustmassa. Voor v = 0 krijg je de massa-energierelatie E = m₀c². Dit is de relativistische rustenergie. De relativistische kinetische energie vind je door deze rustenergie van de totale relativistische energie af te trekken.

[Professor Puntje]

@ always
 
Je vergelijkt appels met peren. De (klassieke) kinetische energie is nul bij een snelheid nul, maar de relativistische energie-inhoud van een deeltje in rust kan best groter dan nul zijn. En voor deeltjes die altijd met de lichtsnelheid reizen is er eigenlijk niet eens een rustenergie, maar voor het rekengemak neemt men dan vaak als rustmassa (en dus rustenergie) nul. Bovendien neemt de relativistische massa van een bewegend voorwerp in tegenstelling tot de klassieke massa toe met de snelheid.
 
Kortom: de vergelijkingen E_k = 1/2 m.v² en E = m.c² lijken qua vorm veel op elkaar maar ze gaan over verschillende zaken (klassieke kinetische energie E_k en totale energie-inhoud E) binnen verschillende theorieën (de klassieke mechanica en de speciale relativiteitstheorie). Geen wonder dat ze niet exact overeenstemmen. Beide vergelijkingen kun je afleiden, en het resultaat is een coëfficiënt 1/2 verschil. Meer redenen heb je in de wetenschap niet nodig. Wellicht dat E = m.c² daarnaast ook nog op een semiklassieke manier uit E_k = 1/2 m.v² kan worden afgeleid, maar dan gaan we het alternatieve pad op. Dat is voor de meer avontuurlijke geesten onder ons wel leuk maar voor het begrip van de gangbare natuurkunde niet nodig, en mogelijk zelfs verwarrend.

[Marko]

 Waarom is dat dan precies 2. Maw wat zorgt ervoor dat de relativistische 'methode' altijd een tweemaal hogere waarde lijkt te geven?

 
Nogmaals:
 
De uitdrukking E=mc² en de uitdrukking E_kin=1/2mv² gaan over 2 verschillende dingen: De laatste over kinetische energie in situaties waar Newtons mechanica geldig is; de eerste is een uitdrukking voor de equivalentie tussen massa en energie die volgt uit de afleiding van kinetische energie in relativistische context.
 
Hoe zit dit precies? Uit de speciale relativiteitstheorie volgt dat de ervaren massa afhankelijk is van de snelheid. De vergelijking E=1/2mv² is een benadering die alleen bij lage snelheden geldt, bij hogere snelheden heeft de snelheid ook invloed op de massa zelf!
 
Je moet kinetische energie schrijven als
 
E=mc²
 
waarbij de term voor m (de ervaren massa) afhankelijk is van de snelheid volgens 
 

\(m=m_0 \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)

 
Daarbij is m0 de massa die je meet als het voorwerp ten opzichte van jou stilstaat (de rustmassa)
 
Dus eigenlijk moet je schrijven:
 

\(E=\frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}\)

 
Dit kun je op een andere manier opschrijven (via een zogenaamde reeksontwikkeling), namelijk als
 

\(E=m_0c^2 + 1/2 m_0v^2 + ...\)

 
In plaats van de puntjes komen er nog andere termen, maar bij niet al te hoge snelheden zijn die verwaarloosbaar klein. Als je je focust op de termen die wel belangrijk zijn, dan zie je daar dus staan, dat de energie het totaal is van een term die onafhankelijk is van de snelheid, en enkel van de rustmassa, plus een term die we al kenden als de kinetische energie in het raamwerk van Newton.
 
De v'tjes en de c'tjes zijn dus niet zomaar uitwisselbaar, en de ene term is echt niet 2 keer zo groot als de ander.
 
Ik hoop dat dit wat licht op de materie laat schijnen.

[always]

"De uitdrukking E=mc² en de uitdrukking E_kin=1/2mv² gaan over 2 verschillende dingen
"
 
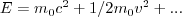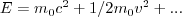Hoewel ze dus over verschillende dingen gaan lijken ze wel bij elkaar opgeteld te kunnen worden?!
 
Kun je daarvan zeggen dat de eerste term de inwendige energie is en de tweede term de kinetisch energie? En zijn de rest van de termen dan uitdrukkingen in c of in v of is alleen de eerste term een c?

[Professor Puntje]

Appels en peren zijn niet hetzelfde, maar het zijn wel allebei vruchten. In die zin kunnen ze opgeteld worden. Dus: "2 appels + 3 peren = 5 appels" is fout; "2 appels + 3 peren = 5 peren"  is ook fout; maar "2 appels + 3 peren = 5 vruchten" is goed. Zo kunnen verschillende soorten energie ook opgeteld worden. Maar of die som in een gegeven geval ook iets zinvols voorstelt is de vraag. Dat zul je dan aan moeten tonen.

[Marko]

"De uitdrukking E=mc² en de uitdrukking E_kin=1/2mv² gaan over 2 verschillende dingen
"

 

Hoewel ze dus over verschillende dingen gaan lijken ze wel bij elkaar opgeteld te kunnen worden?!

 

Dat kan hè. Laten we er een alledaagse situatie bijhalen. Je laat een bal vanaf een bepaalde hoogte op de grond vallen. De eindsnelheid van die bal is uit te rekenen door te stellen dat de potentiële energie (hoogte-energie, m*g*h) wordt omgezet in kinetische energie. Nu gooi je die bal op de grond. Je voegt dus nog een andere vorm van energie toe, namelijk de arbeid die je op de bal uitoefent. De eindsnelheid is nog steeds uit te rekenen, door te stellen dat hoogte-energie + arbeid omgezet zijn in kinetische energie. Op dat moment tel je dus hoogte-energie en arbeid bij elkaar op. 

 

Kun je daarvan zeggen dat de eerste term de inwendige energie is en de tweede term de kinetisch energie? En zijn de rest van de termen dan uitdrukkingen in c of in v of is alleen de eerste term een c?

Zo zou je dat kunnen zien. De tweede term is bij benadering de kinetische energie zoals je die in "gewone" berekeningen tegenkomt.

De andere termen bevatten zowel v als c. De derde term is bijvoorbeeld 3/8 mv⁴/c²

[Michel Uphoff]

\(E=m_0c^2 + 1/2 m_0v^2 + ...\)

Wat je hier dus fraai geïllustreerd ziet is dat de beperkte klassieke wet voor kinetische energie onderdeel uitmaakt van de generieke wet van Einstein. Haal je de eerste term (de energie inhoud van een rustmassa) weg en verwijder je de hogere orde termen van de Taylor reeks omdat deze bij lage snelheden een verwaarloosbare invloed hebben, dan houd je de klassieke kinetische energie formule E_k=0,5mv² over.

 

Als we die appels-peren vergelijking willen gebruiken, zou je kunnen zeggen dat de klassieke mechanica het over een speciaal geselecteerde vrucht heeft, maar Einstein spreekt over alle fruit.

 

Die 0,5 in de klassieke formule is overigens niet van Newton en ook niet dat kwadraat. Newton verklaarde alleen dat de bewegingsenergie evenredig was aan snelheid. 's Gravensande (klik) toonde met valproeven in klei aan dat de grootte van de kuilen bij verdubbeling van de snelheid verviervoudigden, wat door Châtelet (klik) verwoord werd in een formulering die al beter met de werkelijkheid overeen stemde (e=mv²), en het was uiteindelijk de fransman de Coriolis (klik) die E_k=0,5mv² pas in het begin van de 19e eeuw afleidde en het zwaar moest verdedigen. Dus dat die 0,5 in E_k=0,5mv²niet zo voor de hand ligt blijkt wel uit de geschiedenis.

[always]

Ik hoop niet dat ik onnodig in herhaling val en het nog een keer vraag maar het feit dat die half niet voorkomt in de eerste term daar kan toch wel van gezegd worden dat die ontbreekt omdat de deeltjes waar c betrekking op heeft  niet langzamer of sneller gaat dan 300.000km/s?!
 
Mocht het toch allemaal anders zijn, de inwendige energie lijkt me opgeleverd worden door de protonen en neutronen en elektronen die een bepaald atomaire massa eenheid van . Nu kan iets wat massa heeft niet met c gaan dus mijn bovenstaande opmerking kan in die zin eigenlijk niet kloppen. Maar misschien wel benaderen...
Maw in hoeverre worden de nucleonen meegenomen naar massa en in hoeverre naar hun beweging (aangenomen dat ze dus wel heel snel zullen bewegen ín de atoomkern. Of worden ze geacht stil te zitten en alleen hun u omgerekend, of wordt dat in de waarde van u allemaal op een hoop gegooid?

[Professor Puntje]

Die 0,5 in de klassieke formule is overigens niet van Newton en ook niet dat kwadraat. Newton verklaarde alleen dat de bewegingsenergie evenredig was aan snelheid. 's Gravensande (klik) toonde met valproeven in klei aan dat de grootte van de kuilen bij verdubbeling van de snelheid verviervoudigden, wat door Châtelet (klik) verwoord werd in een formulering die al beter met de werkelijkheid overeen stemde (e=mv²), en het was uiteindelijk de fransman de Coriolis (klik) die E_k=0,5mv² pas in het begin van de 19e eeuw afleidde. Dus dat die 0,5 in E_k=0,5mv²niet zo voor de hand ligt blijkt wel uit de geschiedenis.

 
Dat is een interessant stukje geschiedenis. Ik ben direct in mijn boeken gaan snuffelen of daar meer over te vinden is, maar dat viel tegen. Heb je voor die geschiedenis van de kinetische energie behalve de links zelf nog een speciaal boek gebruikt?

[Professor Puntje]

Ik hoop niet dat ik onnodig in herhaling val en het nog een keer vraag maar het feit dat die half niet voorkomt in de eerste term daar kan toch wel van gezegd worden dat die ontbreekt omdat de deeltjes waar c betrekking op heeft  niet langzamer of sneller gaat dan 300.000km/s?!

De logica daarvan ontgaat me. Je hebt het over "de deeltjes waar c betrekking op heeft" en het gegeven dat zo'n deeltje "niet langzamer of sneller gaat dan 300.000km/s". Ik begrijp niet hoe daaruit moet volgen dat je de rustenergie van een massadragend deeltje kunt vinden door bij de klassieke kinetische energie E_k van zo'n deeltje de 1/2 weg te poetsen en zijn bewegingssnelheid v door c te vervangen. Probeer daar eens een (begin van) onderbouwing voor te geven. 

 

Mocht het toch allemaal anders zijn, de inwendige energie lijkt me opgeleverd worden door de protonen en neutronen en elektronen die een bepaald atomaire massa eenheid van . Nu kan iets wat massa heeft niet met c gaan dus mijn bovenstaande opmerking kan in die zin eigenlijk niet kloppen. Maar misschien wel benaderen...

Maw in hoeverre worden de nucleonen meegenomen naar massa en in hoeverre naar hun beweging (aangenomen dat ze dus wel heel snel zullen bewegen ín de atoomkern. Of worden ze geacht stil te zitten en alleen hun u omgerekend, of wordt dat in de waarde van u allemaal op een hoop gegooid?

 

In hoeverre de massa van een atoom gelijk is aan de som van de massa's  van de samenstellende deeltjes kun je zelf uitrekenen...