Systeemidentificatie met naslin

[velgrem1989]

Ik probeer een systeemidentifactie uit te voeren met naslin.

de eerste stap is het uitzetten van ln(KX - y(t))

met KX de versterking maal de stapgrootte , en y(t) de opgemeten stapresponsie.

de volgende stap is om hieruit de eerste tijdsconstante T1 te bepalen en constante A1 (komt van A1*exp(-t/T1))

Dan vervolgens zet je ln(KX - y(t) - A1*exp(-t/T1)) uit en bepaal je T2 en A2.

Nu hier begint mijn probleem. KX = 0.5 in mijn geval , y(0) = 0 en A1 = 3.8

Bij gevolg krijg ik dus bij t=0 : ln (-3.3) wat complexe getallen oplevert (wat niet de bedoeling is)

Iemand een idee wat ik over het hoofd zou kunnen zien of fout doe ? De fout zit volgens mij niet in de overdrachtsfunctie die niet via naslin kan gevonden worden, want ook als ik een voorbeeld uit de cursus wil maken zit ik met hetzelfde probleem, jammer genoeg zie ik de fout niet.

Bedankt

[robertus58a]

Als ik het goed begrijp wil je de parameters van de response in het tijddomein van een tweede orde systeem identificeren.

Hoe is de vergelijking van de response???. Bijvoorbeeld: y = Kx - A1.exp(-t/T1) - A2.exp(-t/T2) ?

[velgrem1989]

Als ik het goed begrijp wil je de parameters van de response in het tijddomein van een tweede orde systeem identificeren.

Hoe is de vergelijking van de response???. Bijvoorbeeld: y = Kx - A1.exp(-t/T1) - A2.exp(-t/T2) ?

Een n-de orde systeem gaat ook , maar dat is inderdaad de respons bij een 2de orde systeem.

Het idee vervolgens van de naslin methode is dat je veronderstelt dat die laatste term veel kleiner is dan de 2 voorgaande ( tijdsconstanten moeten dan voldoende ver uit elkaar liggen ) en dat je dus de benadering maakt:

y = Kx - A1.exp(-t/T1)

dus Kx - y = A1.exp(-t/T1)

dus ln(KX- y) = ln(A1) - t/T1

Vervolgens zet je ln(KX-y) uit in een grafiekje en bepaal je T1 en A1 (dit gaat omdat voor grote waarden van t , ln(KX-y) een rechte benadert) die rechte trek je dan door en dan kan je A1 bepalen door snijpunt met de y-as. T1 bepaal je ook nog maar is voor de verdere redenering niet zo belangrijk.

Vervolgens zeg je dan dat je een benadering hebt gemaakt , en je gaat het verschil bekijken:

y = KX - A1.exp (-t/T1) - A2.exp(-t/T2)

dus KX - y - A1exp(-t/T1) = A2.exp(-t/T2)

dus ln( KX - y - A1exp(-t/T1) ) = ln(A2) - t/T2

nu bijvoorbeeld bij t = 0 is KX bijvoorbeeld 1 , y = 0 (proces is zoals S-curve) A1 > 1 (dit is zo omdat de echte curve afbuigt t.o.v. de benaderende rechte , zie tekening)

dus krijg je 1 - 0 - A < 0

[robertus58a]

ln(KX - y(t) - A1*exp(-t/T1)) uit en bepaal je T2 en A2.

Volgens mij moet je dan: ln(-KX + y(t) + A1*exp(-t/T1)) nemen. Uiteindelijk gaat het om een 2e orde systeem dat je eerst met een eerste orde sys gaat benaderen. Je weet dat het verschil ook weer een exp functie is.

[robertus58a]

In je eerste reactie vroeg je wat er fout ging: Dat is de omgang met + en - tekens. Je kan fouten vermijden door systematisch met de + en - te werken en weten hoe het process model in elkaar zit. Voor een positieve stap verstoring (x=1) en rekening houdende met de process versterking:

\(Positieve\ procesversterking\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Negatieve\ procesversterking\)

\(Kx: \ positief \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Kx: \ negatief\)

\(y=K_x-A_1.e^{-\frac{t}{T_1}}+ A_2.e^{-\frac{t}{T_2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ y=K_x+A_1.e^{-\frac{t}{T_1}}- A_2.e^{-\frac{t}{T_2}}\)

Eerste benadering:

\(ln(Kx-y)=ln(A_1) - \frac{t}{T_1}\ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \\ \ \ \ \ \ \ \ln(y-Kx)=ln(A_1) - \frac{t}{T_1}\)

Tweede benadering:

\(ln(y-Kx+A_1.e^{-\frac{t}{T_1}}) = ln(A_2) -\frac{t}{T_2}} \ \ \ \ \ \ \ \ln(Kx-y+A_1.e^{-\frac{t}{T_1}}) = ln(A_2) -\frac{t}{T_2}} \)

nb. Zowel bij de eerste als de tweede benadering moet de term in het linker lid, tussen de ln-haken, positief zijn. Bij de tweede benadering moet je daarom alleen maar die data meenemen die positief is! Dit is de data aan het begin van de response, het hoogfrequente gedeelte.

[velgrem1989]

In je eerste reactie vroeg je wat er fout ging: Dat is de omgang met + en - tekens. Je kan fouten vermijden door systematisch met de + en - te werken en weten hoe het process model in elkaar zit.

Inderdaad, nu lukt het me wel.

Enorm bedankt!

[Vwodka]

Heeft iemand enig idee waar ik een deftige uitleg kan vinden i.v.m. de methode van Naslin. Bij ons op school hebben we in de les een paar formules opgeschreven, en ook de figuur getekend die hier reeds boven is upgeload maar in onze figuur heb je nog een tweede keer zo'n rechte die meer naar de oorsprong toe staat



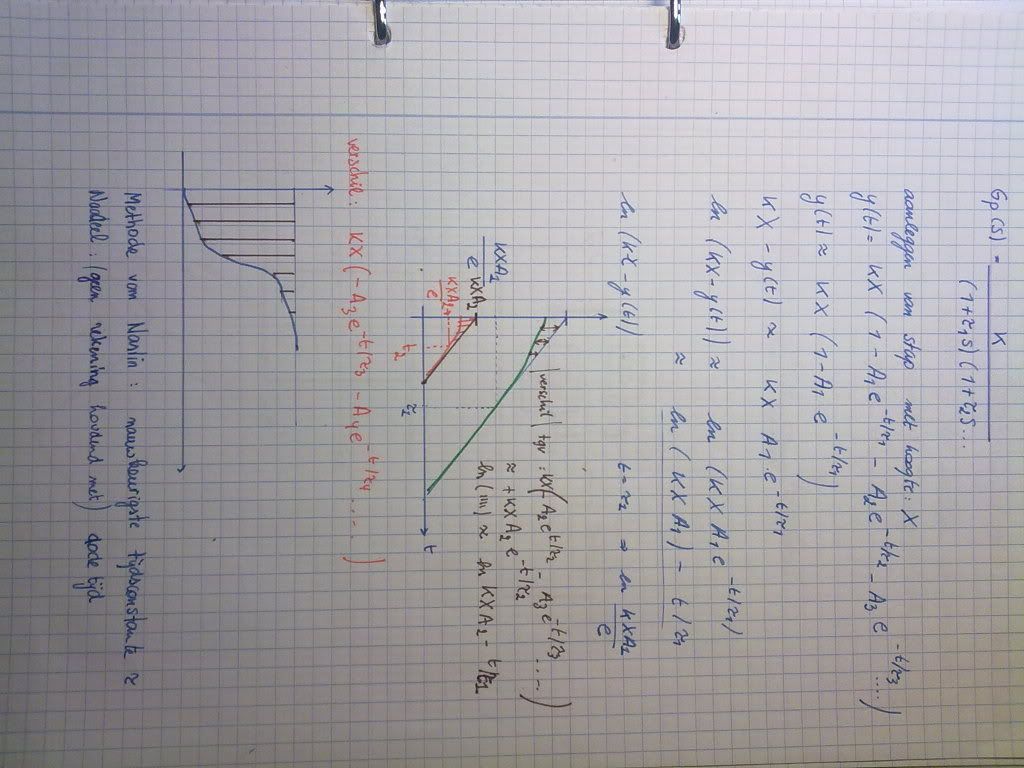
dit is wat we in de les genoteerd hebben

[In physics I trust]

Verplaatst naar praktische wetenschappen.