aufbauprinciple

[aadkr]

Ik heb nooit les gehad in de quantummechanica
Maar ik vind het heel boeiend.
Klopt het aufbauprinciple altijd?
1S 2S 2P 3S 3P 4S 3D 4P 5S 4D 5P 6S 4F 5d 6P 7S 5f 6d 7p 8S
Is dit goed?
Bij voorbaat hartelijk dank.

[sensor]

Volgens de engelse wikipedia berust het aufbauprinciple op het uitgangspunt dat de energieniveau's van de orbitalen exact bepaald kunnen worden met bijvoorbeeld de schrodinger vergelijking. Echter bij zwaardere atomen met heel veel elektronen zijn er geen exacte oplossingen bekend. Met andere woorden het eenvoudige principe van opvullen van de schillen met elektronen voldoet niet meer bij zwaardere elementen.

[Marko]

Ik heb nooit les gehad in de quantummechanica
Maar ik vind het heel boeiend.
Klopt het aufbauprinciple altijd?
1S 2S 2P 3S 3P 4S 3D 4P 5S 4D 5P 6S 4F 5d 6P 7S 5f 6d 7p 8S
Is dit goed?
Bij voorbaat hartelijk dank.

De volgorde die daar staat klopt. Maar het Aufbau-principe wordt niet altijd gevolgd. Zo is de configuratie van Cr [Ar] 4s¹ 3d⁵ waar dat volgens het Aufbau-principe 4s² 3d⁴ zou moeten zijn.

Een houtje-touwtje redeneing: Het is gunstiger om 4s¹ 3d⁵ te hebben, omdat dan alle 5 de 3d-orbitalen evenredig gevuld zitten. Eenzelfde situatie kom je dan ook weer tegen bij koper ([Ar] 4s¹ 3d¹⁰ in plaats van 4s² 3d⁹.

Maar het is maar een houtje-touwtje redenering, want er zijn tal van andere uitzonderingen die zich lastiger laten verklaren.

Dat heeft niet direct te maken met dat er geen exacte oplossingen bekend zijn voor zwaardere elementen. Ten eerste omdat de natuur zich niet veel aantrekt van wat wij een exacte oplossing vinden. Ten tweede omdat die exacte oplossingen er strikt genomen al niet zijn voor alle atomen met meer dan 1 elektron. Ten derde omdat ook voor zwaardere elementen het Aufbau-principe vaak wél gevolgd wordt, dat zou niet moeten kunnen als er aan zou liggen dat er voor zwaardere elementen geen exacte oplossingen bekend waren.

[Benm]

Het Aufbau-concept is iets dat meestal wel klopt, maar inderdaad uitzonderingen kent.

Voor lichte elementen werkt het prima, maar als je richting de overgangsmetalen komt zijn er een aantal atomen die niet helemaal doen we je zou mogen verwachten. Voor de zwaardere elementen zie je hier en daar uitzonderingen, meestal wel verklaarbaar omdat het bijvoorbeeld gunstiger is een hogere schil helemaal te vullen ook al moet je daarvoor 1 electron 'pikken' van een lagere schil.

Spectofotometrie geeft wel inzicht in de daadwerkelijke situatie voor een gegeven element.

Theorie heeft hier ook zo zijn beperkingen: het aufbau principe is gebaseerd op observaties, niet op berekeningen en simulaties. Hoe vreemd het ook lijkt werken simulaties vooralsnog niet voor zware kernen en moleculen. De exacte quantummechanica is niet bekend, voor zover ik weet is momenteel het grootste molecuul dat compleet doorgerekend kan worden H2+ - twee waterstofkernen met 1 electron.

[kwasie]

Het Aufbau-concept is iets dat meestal wel klopt, maar inderdaad uitzonderingen kent.
Theorie heeft hier ook zo zijn beperkingen: het aufbau principe is gebaseerd op observaties, niet op berekeningen en simulaties. Hoe vreemd het ook lijkt werken simulaties vooralsnog niet voor zware kernen en moleculen. De exacte quantummechanica is niet bekend, voor zover ik weet is momenteel het grootste molecuul dat compleet doorgerekend kan worden H2+ - twee waterstofkernen met 1 electron.

:')

[Marko]

Nogmaals, dit zijn 2 verschillende zaken, die weliswaar losjes met elkaar te maken hebben maar het een is echt niet de oorzaak van het ander.

Voor systemen met meer dan 1 elektron worden de golffuncties van deze elektronen niet alleen beïnvloed door elektrostatische interactie met de atoomkern, maar ook door interacties met de overige elektronen. En die interacties hangen op hun beurt weer af van de golffuncties van de elektronen. Dit leidt uiteindelijk tot een stelsel vergelijkingen die zich niet analytisch laten oplossen. Maar ze kunnen wel degelijk worden opgelost, al is er geen eenvoudig recept of algoritme dat in alle gevallen werkt.

Dan het Aufbau-principe. Eigenlijk bedoelt men hier de regel van Madelung, het Aufbauprincipe stelt alleen dat schillen die lager in energie liggen het eerst worden "gevuld". De regel geeft een bepaalde volgorde aan in de energieniveaus. Deze volgorde klopt voor de meeste elementen, maar er zijn uitzonderingen. Die uitzonderingen hebben in veel gevallen te maken met interacties tussen de elektronen. Diezelfde interacties zorgen er ook voor dat de golfvergelijking niet analytisch oplosbaar is, maar het "niet kennen van de quantummechanica" of het niet analytisch kunnen oplossen van de bijbehorende vergelijkingen is niet de oorzaak.

Ware dat wel het geval geweest, dan zou het vanaf helium al mis moeten gaan.

[Benm]

Het is niet zozeer dat het "mis" gaat, op zich is het een prima vuistregel. Of je het Madelung regel of afbau noemt maakt me niet zoveel uit: het idee is dat je kunt voorspellen hoe electronen zich over de schillen in een atoom zullen verdelen.

Voor lichte elementen gaat dit feilloos, en voor de meeste zwaardere elementen strookt het ook gewoon met de werkelijkheid.

Er zijn de handvol elementen waarvoor het niet geldt, en de reden daarvoor is ook wel inzichtelijk, maar ik bedoel te stellen dat deze niet geheel en exact quantummechanisch zijn doorgerekend. Het eerste element waarbij de regel niet werkt is zoals gezegd chroom. Dat heeft al 24 electronen met ieder een golffunctie die van elkaar afhankelijk is, en daarmee lijkt het voorlopig vrij kansloos die op te lossen.

Of het echt onmogelijk is durf ik niet te stellen, als we de golffunctie voor iets met 2 electronen vinden (en daaruit perfect spectraallijnen etc kunnen voorspellen) ligt de weg open naar meer. Niet dat dat direct zoveel extra inzicht oplevert gezien je veel ook experimenteel kunt bepalen, maar wel interessant.

[Marko]

Het is echt onmogelijk, net zo onmogelijk als het drielichamenprobleem.

[Benm]

Daarvan is inderdaad bekend dat het geen universele oplossing kent, al zijn er wel bepaalde 3 body systemen waarvoor wel een oplossing mogelijk is.

Maar of dit ook op gaat voor electronen is toch een iets andere vraag: Gezien de quantificering van de orbitals heb je daarin een stukje minder 'vrijheid' dan bij puntmassa's onder zwaartekracht.

Uiteraard hebben we gewoon de metingen, maar het geeft wel te denken of er een theoretisch model is dat perfect voorspelt in welke situaties een element afwijkt van Madelung/aufbau. Op zich zijn er niet extreem veel uitzonderingen (en sowieso niet zoveel elementen) dat het niet mogelijk is deze domweg te onthouden, maar het zou wel cool zijn als je op grond van een theoretische basis kon voorspellen wat het voor ieder element zou moeten zijn.

[Marko]

Dat is misschien wel een andere vraag, maar wel een die beantwoord is. Het kan niet, er is geen gesloten vorm, punt uit voor systemen met meer dan 1 elektron. Is verder overigens helemaal geen probleem. Numeriek oplossen kan namelijk prima, en we hebben dan ook veel meer dan "gewoon de metingen". Al ruim 50 jaar trouwens.
Omdat de eerste artikelen wat lastig te vinden zijn hier een iets jonger voorbeeld, slechts 45 jaar oud.

[Benm]

Dat is inderdaad een beetje de issue: er is geen gesloten vorm, maar numerieke benadering doet het wel heel goed.

In principe zouden we nu al kunnen berekenen wat de configuraties gaan zijn voor vooralsnog niet aangetoonde elemeten voorbij atoomnummer 118. Overigens zijn die voor de hoogste atoomnummers sowieso al voornamelijk numeriek werk, met halfwaardes in de milli- of microsecondes is daadwerkelijk meten nogal lastig.

[aadkr]

Ik bedrijp nog vele dingen van de quantummechanica niet.
Wat verstaan ze onder de energie van een elektron als het gaat over de elektronenconfiguratie.
Voorbeeld:
32 Ge Germanium
1S2 2S2 2p6 3S2 3p6 4S2 3d10 4p2
hoe weten ze dat de enengie van de elektronen in dit voorbeeld steeds groter wordt.
Wat verstaan we onder de energie van een elektron.
Waarom zie ik bij 1 suborbitaal (bijvoorbeeld p xx ) inhet ene gebied een plus teken staan en in het andere gebied een min teken.
Sorry voor deze domme vragen.
Hoogachtend, aad

[die hanze]

Het zijn geen domme vragen. De reden dat je veel van die dingen niet begrijpt is dat je kwantum mechanica als een chemicus aan het leren bent. Daar is niets mis mee, veel chemici kunnen uit het hoofd heel wat zeggen over de stabiliteit van moleculen zonder berekeningen te doen adhv van allerlei vuistregeltjes. Wil je deze regels echt begrijpen moet je kwantum mechanica echt onder de knie krijgen.

Specifiek over je vraag, je spreekt over de energie van "het elektron". Merk op dat de bindingsenergie van een elektron eigenlijk een potentiaal energie is van het elektron-atoom systeem. Wat ze meestal verstaan onder de energie van het elektron is de energie die nodig is om het elektron los te trekken en naar oneindig te brengen zonder dat het kinetische energie heeft op oneindig.

De bindingsenergie van de elektronen daalt met schil nr, is dat een antwoord op de volgende vraag:?

hoe weten ze dat de enengie van de elektronen in dit voorbeeld steeds groter wordt.

Merk op dat bindingsenergieen negatief zijn en dus een daling van bindingsenergie een netto toename is van de totale energie in het atoom.
Waarom dat zo is volgt uit het oplossen van de schrodinger vergelijking en het pauli principe.

Het volgende is me niet duidelijk wat je bedoelt:

Waarom zie ik bij 1 suborbitaal (bijvoorbeeld p xx ) inhet ene gebied een plus teken staan en in het andere gebied een min teken.

[Marko]

De basis van deze kwantummechanische beschrijving is in de basis dezelfde als de klassieke beschrijving: Het elektron is een geladen deeltje in een elektrisch veld. Het heeft een kinetische en een potentiële energie, en als er verder niets gebeurt kun je stellen dat het totaal van beide constant moet zijn. In de klassieke mechanica kun je met de uitdrukkingen voor kinetische en potentiële energie bewegingsvergelijkingen afleiden die aan deze voorwaarde voldoen.

Het verschil met de klassieke beschrijving is dat slechts bepaalde toestanden, bepaalde energieniveaus zijn toegestaan. En het verschil is dat er geen bewegingsvergelijkingen zijn die bijvoorbeeld de plaats als functie van tijd geven, maar een golfvergelijking ψ die indirect samenhangt met de kans om een deeltje op een plaats aan te treffen. Deze golfvergelijkingen zijn oplossingen van de Schrödinger-vergelijking (meer bepaald: de tijdsonafhankelijke niet-relativistische Schrödinger-vergelijking):



Bovenstaande vergelijking is een eigenwaarde-probeem; de golfvergelijking ψ is een functie die voldoet (eigenfunctie) en E (de energie) is de bijbehorende eigenwaarde. Meerdere functies kunnen voldoen, er zijn dus ook meerdere eigenwaardes. De orbitalen komen nu overeen met deze functies. Ieder orbitaal heeft dus zijn eigen bijbehorende golffunctie, en bijbehorende energie.

De golfvergelijking levert voor iedere coördinaat een zekere waarde. Deze waarde kan positief of negatief zijn, en dat is het teken dat je ziet. Gebieden met een + komen overeen met een gebied waar de functiewaarde van de golfvergelijking positief is.

Ik schreef al dat de golffunctie indirect samenhangt met de kans het elektron op een bepaalde plaats aan te treffen.Het precieze verband is dat deze kans wordt gegeven door het product van de functiewaarde met zijn complex geconjugeerde, maar dat is verder niet zo van belang. Het domein van deze golffunctie is oneindig groot - in theorie kan een elektron dus lichtjaren verwijderd zijn van de kern waar deze "bij hoort", alleen is die kans wel heel erg klein. Hoe dan ook, er is dus sprake van een kansverdeling, met voor iedere coördinaat een bepaalde kans. De plaatjes van de orbitalen zijn nu in feite weergaven van de totale kansverdeling: ze vertonen dat gebied waarin totaal zeg 90% van de verdeling zich bevindt.

Het teken hangt samen met het teken dat de golffunctie op die plaats heeft. Het is niet van belang voor de kans dat je het elektron er aantreft, het verandert niets aan de energie, het is vooral een wiskundig dingetje. TOTDAT je te maken krijgt met chemische bindingen, want chemische bindingen worden beschreven als combinaties van bestaande orbitalen. En voor die combinaties is het teken van de functiewaarde wél van belang. Maar dat is van later zorg, denk ik.

Samenvattend:

Volgens de kwantummechanica worden elektronen in een atoom beschreven aan de hand van een golfvergelijking, die samenhangt met de kans een elektron op een bepaalde plaats aan te treffen. Deze golfvergelijkingen zijn oplossingen van de Schrödingervergelijking, en iedere mogelijke oplossing komt overeen met een bepaalde orbitaal en een bepaalde energie. De plaatjes van de orbitalen zijn een schematische weergave van de kansverdeling die bij dat orbitaal hoort. De + en - verwijzen naar de functiewaarde van de golffunctie op de verschillende plaatsen.


En ja, hoe weten ze nu dat de energie steeds groter wordt? Aan de ene kant omdat dat nu eenmaal uit die Schrödinger-vergelijking komt. Aan de andere kant kun je het ook meten. Slechts bepaalde energieën zijn toegestaan, maar het is wel mogelijk om van het ene energieniveau naar het andere te gaan, als de juiste hoeveelheid energie (het verschil tussen beide niveaus) het systeem in of uit gaat; in de vorm van licht bijvoorbeeld. Via de constante van Planck is deze energie direct te relateren aan de golflengte van licht, dus als je weet bij welke golflengtes een atoom licht uitzendt of absorbeert, kun je beredeneren wat de bijbehorende energieniveaus zijn. In feite is dat het beginpunt geweest van de kwantummechanica.

p.s. of het domme vragen zijn weet ik niet, maar iemand die zoveel mensen met (domme) vragen heeft geholpen mag sowieso ook best een domme vraag terug stellen.

[Marko]

@die hanze: Aadkr doelt op plaatjes als deze:



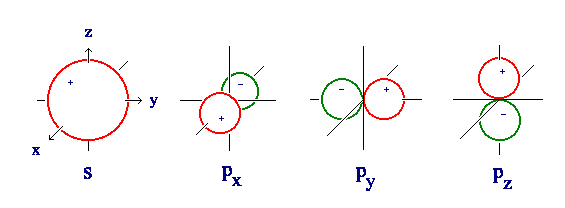
bron: https://chem.libretexts.org/Bookshelves ... _(Dry_Lab)