Hallo,
Zoals jullie misschien weten maken polaroid zonnebrillen gebruik van polarisatie van licht. Zij beschikken over verticale polarisatoren en laten dus alleen verticaal gepolariseerd licht door. Dat er voor verticale polarisatoren is gekozen komt doordat schitteringen in bijv. water (bijna) altijd horizontaal gepolariseerd is.
Nu is mijn vraag waardoor komt het (hoe is het te verklaren) dat die schitteringen horizontaal gepolariseerd zijn?
Ik heb wel iets gelezen over de Brewster Angle, maar ik heb verder niet kunnen uitzoeken hoe precies (als deze er is) de relatie is tussen mijn vraag en die Brewster Angle.
Ik hoop dat jullie hier iets meer over weten te vertellen, mits mogelijk met bron.
Bij voorbaat dank!
Forumregels
(Middelbare) school-achtige vragen naar het forum "Huiswerk en Practica" a.u.b.
Zie eerst de Huiswerkbijsluiter
(Middelbare) school-achtige vragen naar het forum "Huiswerk en Practica" a.u.b.
Zie eerst de Huiswerkbijsluiter
-
Anonymous
- Artikelen: 0
-
DePurpereWolf
- Artikelen: 0
- Berichten: 9.240
- Lid geworden op: wo 12 mar 2003, 19:44
Re: Polaroid zonnebrillen (polarisatie) en schitteringen
Niemand blijkt het te weten dus heb ik het even opgezocht.
Als er licht op water valt, dan zal een deel reflecteren, en een deel absorberen. Als de zon pal op het water staat, wordt alles geabsorbeerd. Maar als de zon erg schuin op het water staat, dan zal een groot deel reflecteren.
Licht van de zon is meestal niet gepolariseerd, ofwel, de golven in de twee dimensies zijn even groot. (de derde dimensie is die waarin het licht in propageert).
Nou zit er dus een verschil van de hoeveelheid reflectie tussen de twee dimensies. Dat is te zien in de volgende grafiek.
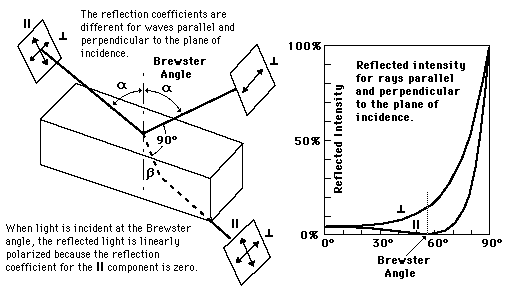
Het is te zien dat bij een bepaalde hoek de reflectie van de dimensie parallel aan het vlak zowat nul is. Bij die hoek wordt dus die dimensie geheel geabsorbeerd en hebben we in de reflectie alleen de loodrechte dimensie over. Die hoek heet de Brewster angle.
Verder kunnen we zien dat de loodrechte altijd boven de parallele dimensie zit. Ofwel, die dimensie wordt altijd minder geabsorbeerd.
Doordat polaroid zonnebrillen deze loodrechte dimensie wegfilterd wordt de reflectie dus veel vermindert.
Maar waarom is die grafiek zoals ie is?
Dat is te verklaren via Fresnel's vergelijking en de wet van Snelius.
De Fresnel vergelijking beschrijft de reflectie en absortptie van electromagnetische golven aan een oppervlak.
De Fresnel vergelijking voor electromagnetische golven in de dimensie parallel aan het oppervlak is de vergelijking:
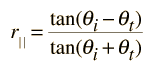
Voor de dimensie loodrecht op het oppervlak is het:
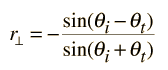
Zoals we in vorige grafiek hebben gezien, is er een punt waarin de vergelijking r|| = 0. Als we dan de formule voor r|| uitrekenen krijgen we een vergelijking met de invlashoek en de hoek van absorptie.
Als we nu ook nog de brekingsindex weten van de ene stof (lucht) en de andere stof (water) dan kunnen we Snellius gebruiken om de hoek van reflectie uit te rekenen daar waar de reflectie, r||, nul is.
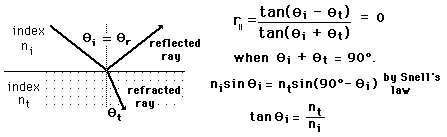Deze hoek noemen ze dan de Brewster hoek.
Als er licht op water valt, dan zal een deel reflecteren, en een deel absorberen. Als de zon pal op het water staat, wordt alles geabsorbeerd. Maar als de zon erg schuin op het water staat, dan zal een groot deel reflecteren.
Licht van de zon is meestal niet gepolariseerd, ofwel, de golven in de twee dimensies zijn even groot. (de derde dimensie is die waarin het licht in propageert).
Nou zit er dus een verschil van de hoeveelheid reflectie tussen de twee dimensies. Dat is te zien in de volgende grafiek.
Het is te zien dat bij een bepaalde hoek de reflectie van de dimensie parallel aan het vlak zowat nul is. Bij die hoek wordt dus die dimensie geheel geabsorbeerd en hebben we in de reflectie alleen de loodrechte dimensie over. Die hoek heet de Brewster angle.
Verder kunnen we zien dat de loodrechte altijd boven de parallele dimensie zit. Ofwel, die dimensie wordt altijd minder geabsorbeerd.
Doordat polaroid zonnebrillen deze loodrechte dimensie wegfilterd wordt de reflectie dus veel vermindert.
Maar waarom is die grafiek zoals ie is?
Dat is te verklaren via Fresnel's vergelijking en de wet van Snelius.
De Fresnel vergelijking beschrijft de reflectie en absortptie van electromagnetische golven aan een oppervlak.
De Fresnel vergelijking voor electromagnetische golven in de dimensie parallel aan het oppervlak is de vergelijking:
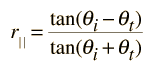
Voor de dimensie loodrecht op het oppervlak is het:
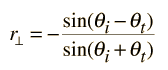
Zoals we in vorige grafiek hebben gezien, is er een punt waarin de vergelijking r|| = 0. Als we dan de formule voor r|| uitrekenen krijgen we een vergelijking met de invlashoek en de hoek van absorptie.
Als we nu ook nog de brekingsindex weten van de ene stof (lucht) en de andere stof (water) dan kunnen we Snellius gebruiken om de hoek van reflectie uit te rekenen daar waar de reflectie, r||, nul is.
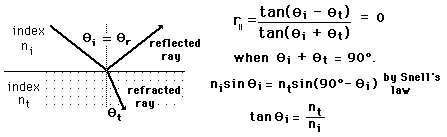Deze hoek noemen ze dan de Brewster hoek.-
Anonymous
- Artikelen: 0
Re: Polaroid zonnebrillen (polarisatie) en schitteringen
Bedankt voor deze informatie! 
