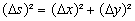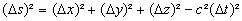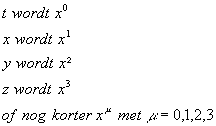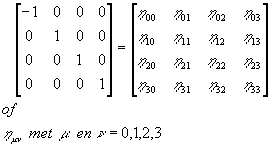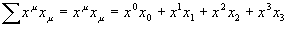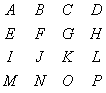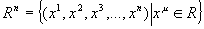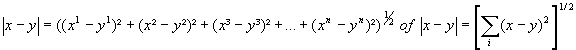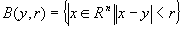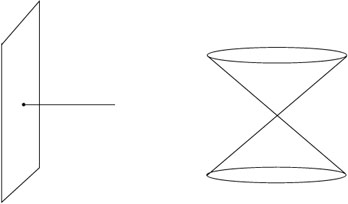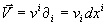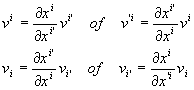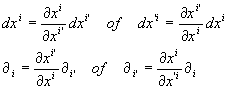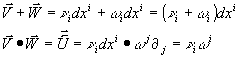Les 2 Variëteiten
In deze les gaan we het fundament van de algemene relativiteitstheorie behandelen: Met name het concept ruimtetijd en hoe dit wiskundig beschreven wordt door het begrip varieteit. We zullen van elementaire wiskundige begrippen vertrekken om deze ruitetijd op te bouwen. Ook hier is de boodschap weer om alle begrippen goed tot je te laten doordringen. Dit hoofdstuk is nog erg beschrijvend, maar als we later de wiskundige machinerien er op los laten is het soms handig om de fundamentele concepten die er achter zitten in herrinering te brengen.
2.1 Gebeurtenissen
Op 18 juni 1815 werd Napoleon definitief verslagen te Waterloo. Op 9 november 1989 valt de muur van Berlijn. Op 14 juli 1789 wordt de Bastille in Parijs bestormt. Ondanks hun grote invloed op onze westerse geschiedenis van deze feiten, staan ze hier enkel maar om het begrip gebeurtenis duidelijk te maken: Een feit éénduidig bepaald in ruimte en tijd.
We moeten echter opletten dat we die éénduidige bepaling van ruimte en tijd niet verwarren met de aanduiding van plaats en tijdstip.
Laat me dit verduidelijken. De slag van Waterloo vond voor ons plaats op 18 juni 1815. Voor de chinezen is de veldslag in het jaar 4513 beslecht. Ondanks de twee verschillende tijdsaanduidingen heeft de slag bij Waterloo slechts op één bepaald moment plaatsgevonden.
We zouden kunnen stellen dat om over een gebeurtenis te spreken er een waar en wanneer moet zijn maar dat deze niet gekend hoeft te zijn. Het aanduiden van een gebeurtenis met een label, bv "Slag bij Waterloo" is op dit ogenblik voldoende.
Ook in de natuurkunde en specifiek in de algemene relativiteitstheorie werken we met het begrip gebeurtenis. Waar historici echter triviale zaken , het zaaien van wat koren door boer Jan, niet als een gebeurtenis beschouwen, zullen natuurkundigen elke plaats op elk ogenblik als een gebeurtenis beschouwen.
2.2 Een verzameling van gebeurtenissen
Een handige manier om jezelf te ondervragen ter voorbereiding van een toets geschiedenis, is het opschrijven van gebeurtenissen op een papiertje zonder tijd of plaats. Deze steek je dan in een plastic zak of sigarenkistje om er willekeurig één uit te trekken. De bedoeling is dan om plaats en tijd op te dreunen.
Het sigarenkistje of de plastic zak is wat wiskundigen een verzameling van gebeurtenissen noemen.
Losse feiten zonder aanduiding van plaats of tijd. Een verzameling hoeft niet alle gebeurtenissen te bevatten. Zo kun je een verzameling "Europese geschiedenis" maken of een verzameling "De Reformatie" maken.
Ook in de natuurkunde zullen we de gebeurtenissen in een verzameling stoppen. Met wat flexibiliteit zou je deze verzameling reeds de "ruimtetijd" kunnen noemen.
2.3 Topologie van een verzameling
Nu zal elke geschiedenis leraar je weten te vertellen dat het nogal zinloos is om gebeurtenissen los van elkaar te zien. En dat je deze moet kunnen plaatsen in hun context. Hij zal terecht opmerken dat gebeurtenissen uit elkaar voortvloeien of invloed op elkaar uitoefenen. Hij zal voorstellen om over een bepaalde plaats, bijv het romeinse rijk, een tijdslijn op te stellen. We ordenen dan de gebeurtenissen door oorzaak voor gevolg te plaatsen. U merkt op dat we dit kunnen doen zonder er een exacte tijdsbepaling bij te plaatsen, al zullen historici dit het lifst wel doen. Maar om te ordenen is dit niet echt nodig.
Het aanbrengen van zo'n ordening noemen we in de wiskunde het aanbrengen van een topologie.
Buiten het ordenen van oorzaak en gevolg , kunnen we de verschillende tijdslijnen nog eens ordenen naar plaats. Dit is de ordening "ligt naast"
Waar we de causale (oorzaak en gevolg) ordening nog met één set getallen kunnen aanduiden (gebeurtenis 1 komt voor gebeurtenis 2 komt voor
) hebben we voor de plaatssen op onze wereldbol 2 sets van getallen nodig (vb breedte- en lengtegraad). Wiskundig zeggen we dat de causale of tijdsordening ééndimensionaal is en de plaatsordening 2 dimensionaal. We introduceren op de verzameling van "wereldgebeurtenissen" een driedimensionale topologie.
Ook onze "pre-ruimtetijd" verzameling gaan we uitrusten met een topologie. Dat deze vierdimensionaal is zal jullie niet verwonderen!
2.4 De varieteit of manifold
We zijn dus vertrokken van losse gebeurtenissen die we in een verzameling hebben gestopt. Daarna hebben we in deze verzameling en ordenng aangebracht ,een topologie. Onze historici zouden met een beetje goede wil voldoening kunnen nemen indien we hier zouden stoppen. Het zal wel wat onhandig zij om niet met dat te kunnen werken, maar de chronologie van de gebeurtenissen is wel aanwezig en dat is toch de essentie van geschiedenis.
Onze natuurkundigen zijn echter minder gelukkig. Uiteindelijk willen ze een model van de werkelijkheid waarmee ze kunnen rekenen , numerieke oplossingen vinden. De oplossing hiervoor is dat we de ordening gaan uitwerken met getallen.
Een voorbeeld: We hebben eenverzameling met 16 gebeurtenissen A tot en met P.
We brengen hier een 2 dimensionale ordening aan. Dit doen we als volgt: A( ligt naast B,ligt naast E), B(ligt tussen A en C, ligt naast F)
. F(ligt tussen E en G, ligt tussen Ben J)
We kunnen dit visualiseren met volgend beeld.
We kunnen echter de ordening ook aanduiden met de gehele getallen en stellen dat A(1,1) B(1,2) C(1,3)
F(2,2). Hierbij veronderstellen we dat de ordening van de gehele getallen volgen en dus dat 2 ligt tussen 1 en 3. Wiskundig zeggen we dan dat de ordening lijkt op de ordening van de gehele getallen.
Voor onze ruimtetijd volstaan de gehele getallen echter niet om al onze gebeurtenissen te ordenen. We ervaren ruimte en tijd immers als iets continu. Daarom zullen we stellen dat de topologie van onze ruimtetijd moet lijken op de topologie van R
4, de vierdimensionale ruimte van reële getallen.
Een verzameling uitgerust met een topologie die lijkt op die van Rn noemen we een varieteit (of manifold in de engelse literatuur).
De grote kracht van een variteit is dat alle rekenkunde die we op Rn kunnen toepassen, ook op de varietiet kunnen toepassen!
In de volgende paragrafen gaan we dit alles in een wiskundig jasje gieten, hou hierbij steeds de bovengaande beschrijving voor ogen en probeer te kijken wat er achter de wiskundige symbolen zit.
2.5 De wiskundige vertaling.
Eerst gaan we wat vertellen over de eigenschappen van de n-dimensionale euclidische ruimte R
n. Dit is gewoon de verzameling van alle n-paren van de reele getallen:
De topologische "afstand" tussen twee elementen (in de ruimtetijd gebeurtenissen) y en z is dan :
Met deze "afstand" (Ik zet dit bewust tussen anhalingstekens omdat afstand niet verward mag worden met lengte. Lengte is immers een eigenschap die samenhangt met assenstelsels) kunnen we het begrip open bol definieren.
Een open bol is de verzameling van alle punten in R
n die vallen binnen een bepaalde afstand r van het punt y. (In R
3 is dit inderdaad een bol).
Een open verzameling is een verzameling die opgebouwd is uit de unie van een willekeurig (mogelijks oneindig) aantal open bollen.
Ruwweg gesproken is een open verzameling het binnenste van een gesloten (n-1) oppervlak.
Het definieren van het begrip open verzamelingen in R
n, rust R
n ook in één keer uit met een topologie. Met de open bollen kun je immers bepalen welk punt meer in de nabijheid ligt dan een ander punt.
Enkele voorbeelden van open verzamelingen binnen R
n
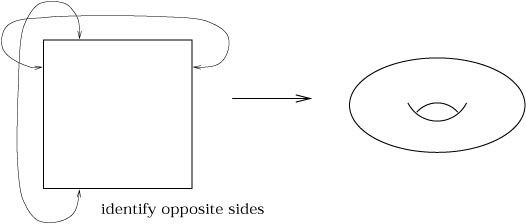
De torus, die je kunt opbouwen door van een vlak de tegenovergestelde zijden aan elkaar te plakken is een open verzameling
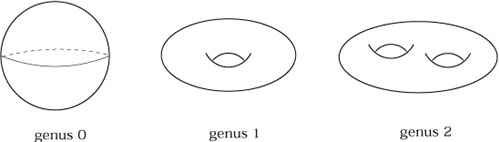
Een Riemann oppervlak met genus g is een open verzameling
Een dubbele conus of een oppervlak waar een lijnstuk uitsteekt is geen open verzameling
Nu we een topologie hebben voor R
n kunnen we gaan kijken hoe we de topologie van andere verzamelingen laten lijken op die van R
n.
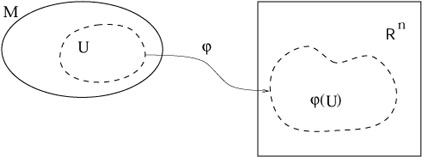
Hiervoor grijpen we terug uit naar een elementair begrip uit de verzamelingenleer: De map tussen twee verzamelingen.
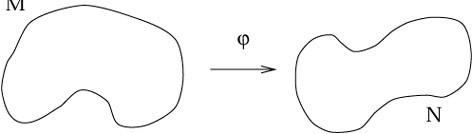
Gegeven twee verzamelingen M en N , dan is de map een relatie die aan elk element van M juist één element van N verbindt. Of anders gezegd een map is een generalisatie van de functie.
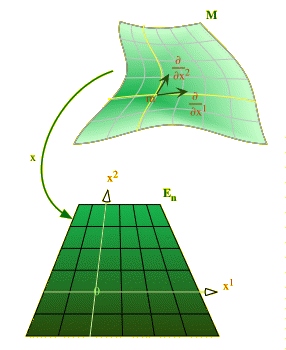
Door nu een éénduidige map te maken tussen R
n en een willekeurige verzameling definieren we automatisch een topologie op die verzameling:
In het volgende hoofdstuk gaan we hier nog dieper op in.
2.6 Besluit
Om een theorie op te stellen over een natuurkundig systeem moeten we eerst een kader scheppen waarin het systeem kan beschreven worden. Voor de gravitatie blijkt een vierdimensionale continue wiskundige ruimte voldoende te zijn als wiskundig kader.
Door deze ruimte in te richten naar het voorbeeld van de euclidische ruimte , wordt het mogelijk om reeds bestaande wiskunde toe te passen op dit kader.
In volgende hoofdstukken zullen we zien hoe dit concreet in zijn werk gaat. We zullen hiervoor coördinatensystemen introduceren en wiskundige objecten die we tensoren noemen.