Bij deze cursus zijn ook een aantal oefenopgaven gemaakt, deze vind je onder de cursus.
Als je van deze cursus gebruik maakt, willen we je vriendelijk vragen te laten weten wat je er van vond:
- Geef eventuele foutjes aan;
- Zijn de onderdelen soms onduidelijk, of net erg helder?
- Ontbreken er volgens jou stukken, of heb je suggesties?
- ...
---------------------------------------------------------------------------------------
[microcursus] WARMTECAPACITEIT deel 2: de rekenbladmethode
Auteur: Jan van de Velde
Trefwoorden: calorimeter, joulemeter, calorimetrie, warmteberekening, energiebalans, warmtestroom, warmtebalans, temperatuur, warmtecapaciteit, soortelijke warmte, latente warmte, smeltwarmte, verdampingswarmte
1: Inleiding
Deze tweedelige basiscursus is bedoeld voor (middelbare school) leerlingen die moeite hebben met rekenwerk rond de calorimeter. Een aantal begrippen zoals entropie, enthalpie, arbeid e.d. komen op dit niveau niet of nauwelijks aan de orde, en ook andere zaken worden gewoonlijk versimpeld. Zo ook hier.
In dit deel 2 gaan we leren sommetjes op te lossen zoals:
"In een vat met een warmtecapaciteit van 75 J/K zitten 500 g water en 100 g ijs van 0,0 °C.
Bereken de massa stoom van 115°C die men aan het mengsel moet toevoegen om water van 40 °C te krijgen."
Dit zijn eigenlijk meerdere sommetjes uit deel 1, samengevouwen tot één probleem. Hier raken velen de weg kwijt in de veelheid van gegevens en resultaten van tussenstappen. Een manier om overzicht en logica hierin te brengen is het gebruiken van een rekentabel. Bereken de massa stoom van 115°C die men aan het mengsel moet toevoegen om water van 40 °C te krijgen."
In deel I van de cursus bespraken we de onmisbare basisbegrippen temperatuur, warmte, warmtecapaciteit, latente warmte. Deze begrippen beschouwen we voor dit deel 2 als voorkennis. We raden je dus aan om deel 1 door te nemen, want een paar kleine misverstandjes, of "slechte (reken)gewoontes" zijn meestal de reden dat je vastloopt in de wat ingewikkelder berekeningen.
Ook is het onmisbaar dat je formules kunt ómschrijven, bijvoorbeeld van v=s/t naar s=vxt.
Neem zonodig eerst de [microcursus] formules herschrijven / vergelijkingen oplossen door.
| De waarden voor soortelijke warmte enz. die we in deze cursus gebruiken komen voornamelijk uit : Onderaan de cursus vind je nog oefenopgaafjes, met het antwoord gegeven, maar met de uitwerking verborgen. Die uitwerking kun je zichtbaar maken door op de bijbehorende link "Verborgen inhoud" te klikken. | <!--start boeklink--> Binas Havo VWO / druk 5<!--einde boeklink--> |
Misschien is deze stof niet nieuw voor je, en mogelijk leerde je de formules:
\(Q_{in} = Q_{uit}\)
met:
\(Q_{in} = m\cdot c \cdot(T_{eind}- T_{begin})\) en \(Q_{uit} = m\cdot c \cdot(T_{begin}- T_{eind})\) (dus met Tbegin en Teind in omgekeerde volgorde)
VERGEET ZE !!! . in deel 1 van deze cursus bespraken we uitvoerig een paar andere: met:
\(Q_{in} = m\cdot c \cdot(T_{eind}- T_{begin})\) en \(Q_{uit} = m\cdot c \cdot(T_{begin}- T_{eind})\) (dus met Tbegin en Teind in omgekeerde volgorde)
Behoud van energie:
verandering van temperatuur:
\(Q_1 + Q_2 + Q_3 + {.......} = 0\)
\( \Delta T = T_{eind} - T_{begin} \)
En dan nog drie, die érg op elkaar lijken (zie ook § 5.3)
Warmtecapaciteit:
Soortelijke warmte(capaciteit):
Latente warmte (verdampen, condenseren, smelten, stollen) :
\( Q = C \cdot \Delta T \)
\( Q = m \cdot c \cdot \Delta T\)
\( Q = m \cdot L \)
In de bijlage onderaan vind je de grootheden, eenheden, symbolen en definities nog eens kort op een rijtje.
3: Tussenstappen: koud en warm water mengen:
We zagen al, als je twee voorwerpen/stoffen van verschillende temperatuur met elkaar in contact brengt, dan zal er warmte gaan stromen van hoge temperatuur naar lage temperatuur, totdat er één evenwichtstemperatuur (gezamenlijke eindtemperatuur) ontstaat.
"We voegen 3 kg water van 20°C samen met 1 kg water van 80°C. Wat wordt de eindtemperatuur?"
Zoiets kun je netjes wiskundig oplossen:
gegeven
stof 1: m1 = 3 kg, T1b = 20°C
stof 2: m2 = 1 kg, T2b = 80°C
gevraagd
evenwichtstemperatuur: Te = T1e = T2e
oplossing
- basisvergelijking voor warmtebehoud:
- maar c1 = c2 = c (wegdelen):
- oplossen naar de enige onbekende te, gegevens invullen en uitrekenen:
Maar misschien ben je daar niet zo'n held in. In dat geval zou je het stap voor stap kunnen doen zodat je één voor één je 5 eenvoudige formuletjes kunt toepassen. In alle gevallen kan dat vrij simpel, tenminste als je onderweg een of meerdere tussenstappen toepast.stof 1: m1 = 3 kg, T1b = 20°C
stof 2: m2 = 1 kg, T2b = 80°C
gevraagd
evenwichtstemperatuur: Te = T1e = T2e
oplossing
- basisvergelijking voor warmtebehoud:
\(\begin{array}{*{20}{l}} {{Q_1} + {Q_2} = 0} & { \Leftrightarrow {c_1}{m_1}\Delta {T_1} + {c_1}{m_2}\Delta {T_2} = 0} \\ {} & { \Leftrightarrow {c_1}{m_1}\left( {{T_{1e}} - {T_{1b}}} \right) + {c_2}{m_2}\left( {{T_{2e}} - {T_{2b}}} \right) = 0} \\\end{array}\)
- maar c1 = c2 = c (wegdelen):
\({m_1}\left( {{T_e} - {T_{1b}}} \right) + {m_2}\left( {{T_e} - {T_{2b}}} \right) = 0\)
- oplossen naar de enige onbekende te, gegevens invullen en uitrekenen:
\({T_e} = \frac{{{m_1}{T_{1b}} + {m_2}{T_{2b}}}}{{{m_1} + {m_2}}} = \frac{{3.20 + 1.80}}{4} = 35°C\)
Een vaak toegepaste tussenstap: We brengen de stoffen waar we van uitgaan (noemen we beginstoffen, hier 3 kg water van 20°C en 1 kg water van 80°C), eerst en vooral naar één en dezelfde temperatuur. Welke temperatuur we daarbij kiezen is voor de uitkomst niet belangrijk, zolang onze stoffen daarbij maar niet van fase zouden veranderen.
De warmte die dat oplevert slaan we even op (bijv. in een spaarvarken
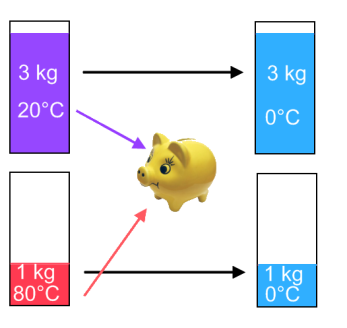 (afb. 1)
(afb. 1)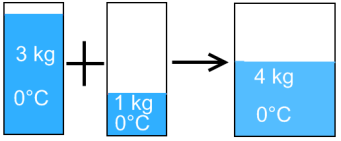 (afb. 2)
(afb. 2) (afb. 3)
(afb. 3)4: De rekentabel
Door die tussenstappen vermijden we al dat we ingewikkelde formules krijgen. Nu nog overzicht over onze gegevens, en makkelijk een plek zien te vinden om mee te beginnen. Voor al die gegevens en dat zoek- en rekenwerk kunnen we een overzichtelijk rekenblad maken. Het principe is je ongetwijfeld bekend uit computerprogramma's als Excel:
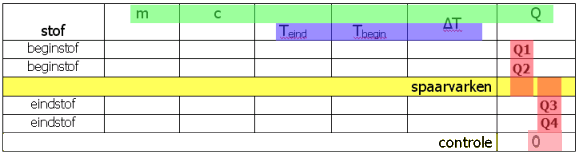 (afb. 4)
(afb. 4)Hierin kun je ál je gegevens - en je tussenuitkomsten !! - kwijt. Herken je trouwens de drie formules? a
............. Q=m·c·ΔT ............. ΔT=Teind - Tbegin ............. Q1 + Q2 + Q3 + .... = 0
De spelregels hiervoor zijn best logisch:
- bepaal hoeveel "verschillende stoffen" er in je opgave zitten. Een "stof" noemen we hier alles waarvoor je een aparte massa (m), en/of een aparte soortelijke warmtecapacteit ( c ), en/of aparte temperaturen (T), en/of aparte warmte (Q) voor gegeven of gevraagd krijgt.
- maak een tabel met voor elke "stof" een eigen regel.
- vul in elk veld in wat je weet. Gegevens als soortelijke warmtecapaciteit moet je misschien uit een tabellenboek halen.
- kijk welke tussenstappen nodig of mogelijk zijn . In dit geval is het een handige tussenstap om je beginstoffen allemaal naar één willekeurige eindtemperatuur te brengen. Deze eindtemperatuur is dan de begintemperatuur voor je eindstof. (een handig gekozen temperatuur bespaart je overigens wat rekenwerk)
- kijk dan regel voor regel en kolom voor kolom welk leeg vak je zou kunnen berekenen aan de hand van andere gegevens in de regel of kolom.
- herhaal stap 5 totdat je tabel helemaal gevuld is.
stap 1:
Hier zijn dat dus drie "stoffen", want van koud en warm water krijg je aparte massa's én temperaturen, en van het resultaat, mengwater, wordt de temperatuur gevraagd.
stap 2:
De kolommen in de tabel zijn áltijd dezelfde, want we werken altijd met dezelfde formules.
stap 3:
Invullen is een kwestie van zorgvuldig je opgave lezen.
stap 4:
Je zag bij het opwarmen en afkoelen al dat het niks uitmaakt hoever je opwarmt, als je maar weer evenver afkoelt. We kunnen dus ons warme en koude water (beginstoffen) eerst op een nieuwe eindtemperatuur brengen, en diezelfde temperatuur gebruiken als begintemperatuur van ons mengwater(eindstof). Je kunt een willekeurige temperatuur kiezen zolang je maar geen smelt-of kookpunten overschrijdt. Hier kiezen we 0°C (niet de handigste) . Nogmaals, de som van alle warmtestromen moet 0 zijn, dus dat komt vanzelf goed uit, wat je ook kiest.
Dat ziet er dan voorlopig zó uit:
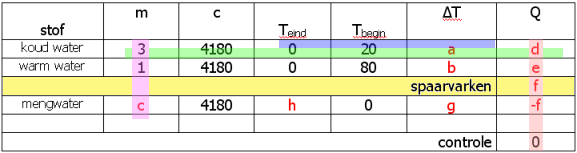 (afb. 5)
(afb. 5).................... Q=m·c·ΔT .................... ΔT=Teind - Tbegin .................... Q1 + Q2 + Q3 + .... = 0
Stap 5 en 6:
We gaan nu simpelweg per regel en per kolom stap voor stap kijken wat we kunnen uitrekenen, dat wil zeggen, in welke "formules" we maar één onbekende hebben. Uit het een volgt dan het ander, en met minimaal nadenken en een minimaal risico op fouten kun je in eenvoudige stappen heel de tabel volrekenen: Neem de tabel maar eens over op een kladje, zonder de rode letters, en reken mee.
ΔT mag al geen probleem zijn:
a wordt 0-20 = -20 K,
b wordt 0-80 = -80 K (let op de minnetjes!!)
De massa mengwater :
c wordt 3 kg koud + 1 kg warm = 4 kg.
nou kunnen we makkelijk Q uitrekenen voor het koude en het warme water:
d wordt Qkoud = 3 x 4180 x -20 = - 250 800 J ,
e wordt Qwarm = 1 x 4180 x -80 = - 334 400 J (let op de minnetjes !!)
Nu hebben we alle gegevens voor het spaarvarken:
f wordt Q = - 250 800 - 334 400 = - 585 200 J
heel dat spaarvarken mag in het mengwater leeggekiept worden
-f wordt Qmeng = + 585 200 J (controle: spaarvarken + Qmeng = 0 )
Nu kunnen we makkelijk van het mengwater uitrekenen :
g wordt ΔTmeng = + 585 200 /(4 x 4180) = +35 K
En tenslotte de eindtemperatuur van het mengwater:
h wordt Teind= 0°C + (+35) = +35°C :eusa_whistle:
Eindresultaat:
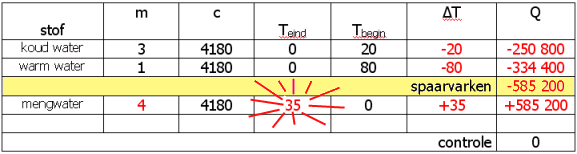 (afb. 6)
(afb. 6)Vul dezelfde tabel nou eens in, waarbij je dan in plaats van 0°C als tussentemperatuur bijvoorbeeld 10°C kiest, of 20°C (ook wel leuk) of 80°C of ook vooral interessant: 35°C. Snap je steeds wat je getallen betekenen?
Wil je nog beter nieuws? Nou, dit was eigenlijk wel 90 % van de cursus. We willen je alleen nog een paar logische tussenstappen laten zien voor wat speciale gevallen.
5: De calorimeter
Proefjes zoals hierboven spelen zich natuurlijk niet in het luchtledige af. Dat gebeurt in een vat, en dat vat heeft zelf zo ook zijn eigen (voorwerps)warmtecapaciteit. Dat ding zal dezelfde temperatuur krijgen als de stoffen die erin zitten, en daarvoor ook warmte opnemen of afstaan.
5.1 De calorie
De calorie is de oude eenheid van energie, gedefinieerd als de hoeveelheid warmte (1 cal) nodig om 1 g water 1 K in temperatuur te laten stijgen. Als je even rekent met de soortelijke warmtecapaciteit van water zoals we die nu kennen, afgerond 4200 J/kg·K , dan zie je dat een calorie overeenkomt met 4,2 J (officieel 4,184 J).
Uit gewoonte wordt de calorie nog wel gebruikt in de voedingsleer, je komt hem overal nog tegen op verpakkingen van voedingsmiddelen. Pas op, in de voedingsleer gebruiken ze vaak de "Cal" (met hoofdletter c), wat eigenlijk kilocalorie (kcal) betekent, en maar al te vaak wordt (slordig) die hoofdletter dan ook nog vergeten. Als je in een damesblad leest dat een mokkagebakje 360 caloriën levert (dat zou dat een heel mager gebakje zijn, want met 360 cal krijg je 2 kopjes water nog geen graad opgewarmd) wordt dus 360 kcal ofwel ca. 1 500 000 J bedoeld.
5.2 Het apparaat
De naam "calorimeter" (zonder "e") is afgeleid van "Calor", latijn voor warmte. In zijn eenvoudigste vorm is het een goed geïsoleerd potje met een thermometer om de temperatuur van de inhoud te kunnen bepalen. Er kan (idealiter) geen warmte in of uit, daar binnenin heb je dus een gesloten systeem waaraan je kunt meten en rekenen. Daar komen al die sommetjes vandaan.
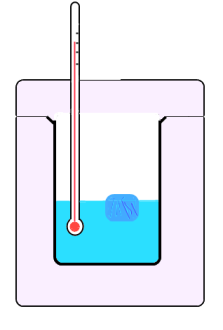 (afb. 7) een eenvoudige calorimeter
(afb. 7) een eenvoudige calorimeterHet potje is vaak van glas, aluminium of roestvaststaal, en dat is omgeven met isolatiemateriaal of, zoals in een thermoskan, door een vacuüm. Vaak worden nog andere doorvoeren in het deksel gemaakt, bijvoorbeeld voor een roerwerkje, een verwarmingselementje (dompelaar) of iets dergelijks.
Mogelijk kom je ook nog wel eens de termen "bomcalorimeter", "vlamcalorimeter" of "reactiecalorimeter" tegen. Die gebruik je voor wat ingewikkelder proeven dan het smelten van een ijsklontje. We gaan nu niet verder op de details daarvan in.
5.3 De calorimeter in de rekentabel: de eindtoestand van twee totaal verschillende stoffen
Het potje en de thermometer krijgen natuurlijk altijd dezelfde temperatuur als de inhoud. Uiteraard heeft het materiaal van het potje, het isolatiemateriaal er direct rond en ook de andere apparatuur die er mogelijk ingebouwd wordt, zijn eigen soortelijke warmtecapaciteit. Dat neemt dus ook energie op als het opwarmt.
Een calorimeter bestaat niet alleen uit dat potje. Voor nauwkeurige metingen wordt dus heel netjes voor het hele apparaat inclusief alle extra's bepaald hoeveel warmte er nodig is om het apparaat zélf 1 K in temperatuur te doen stijgen. Zoals hierboven is de massa hier al in verrekend, het apparaat verandert nooit, dus de massa doet niet meer terzake. De voorwerpswarmtecapaciteit "C" wordt daarom uitgedrukt in joule per kelvin (J/K).
Stel dat de isolatie perfect is, en het potje van aluminium (calu = 880 J/kg·k) gemaakt is en 100 g weegt.
De extra's (roerwerk e.d.) wegen 50 g, en zijn bijvoorbeeld van koper (ckoper = 387 J/kg.K)
Een simpele berekening leert je dat de voorwerpswarmtecapaciteit dan zal zijn:
Ccalorimeter = mpotje x cmateriaal potje + mextra's x cmateriaal extra's
..................= 0,100 (kg) x 880 (J/kg·K) + 0,050 (kg) x 387 (J/kg·K)=
..................= 88 + 19,4 = 107,4 (J/K)
Voor elke graad dat de inhoud in temperatuur moet stijgen heeft de calorimeter dus zelf ook 107,4 J energie nodig!..................= 0,100 (kg) x 880 (J/kg·K) + 0,050 (kg) x 387 (J/kg·K)=
..................= 88 + 19,4 = 107,4 (J/K)
Met andere woorden, de (voorwerps)warmtecapaciteit C van de calorimeter is 107,4 J/K.
Daarmee valt hopelijk een overeenkomst op tussen onze drie formules:
<table cellpadding="0" cellspacing ="0" border="1" class="bbc">[tr][td]soortelijke warmtecapaciteit[/td][td]Q =[/td][td]m x[/td][td]c x[/td][td]ΔT[/td][td] [/td][/tr][tr][td](voorwerps) warmtecapaciteit[/td][td]Q =[/td][td] [/td][td]C x[/td][td]ΔT[/td][td](massa zit al in C verrekend)[/td][/tr][tr][td]latente warmte[/td][td]Q =[/td][td]m x[/td][td]L [/td][td] [/td][td](geen temperatuursverandering)[/td][/tr]</table></div>
Voor elke formule gebruiken we een vergelijkbare constante, de c, C of L, die afhangt van de stof of het voorwerp waar het over gaat. Dat is makkelijk voor onze tabel: de kolom waar we hierboven nog steeds onze soortelijke warmtecapaciteit c invulden kan net zo goed voor de andere constanten worden gebruikt. Als we een regel gaan invullen moeten we wél in de gaten houden:
Voor elke formule gebruiken we een vergelijkbare constante, de c, C of L, die afhangt van de stof of het voorwerp waar het over gaat. Dat is makkelijk voor onze tabel: de kolom waar we hierboven nog steeds onze soortelijke warmtecapaciteit c invulden kan net zo goed voor de andere constanten worden gebruikt. Als we een regel gaan invullen moeten we wél in de gaten houden:
- op een regel voor (voorwerps)warmtecapaciteit C: de massa van het voorwerp zit al in C verrekend en doet er dus niet toe.
- op een regel voor latente warmte L: er is geen ΔT, en dus ook geen Tbegin of Teind.
- op een regel voor soortelijke warmtecapaciteit c: álle kolommen zijn belangrijk.
Een oefening dan maar:
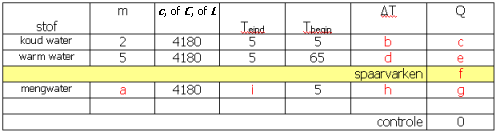
" Een calorimeter (C = 209 J/K) met een temperatuur van 18°C wordt gevuld met 500 g water met een temperatuur van 10°C. Wat is de eindtemperatuur van de calorimeter met water?"
De gegevens inschrijven levert deze tabel op:
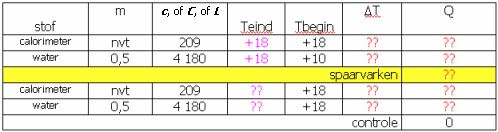 (afb 8)
(afb 8)Tot en met het spaarvarken kunnen we alles berekenen:
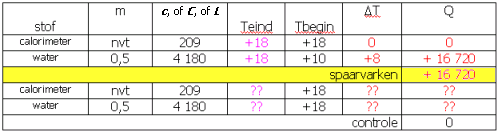 (afb 9)
(afb 9)Hier zitten we even vast, want calorimeter en water kunnen nooit één eindstof worden.
Maar we zouden wel in een tussenstap kunnen berekenen hoeveel warmte het zou kosten om de calorimeter én de 500 g water 1K in temperatuur te verhogen. Eigenlijk bereken we dan de (voorwerps)warmtecapaciteit van het voorwerp "calorimeter met 500 g water", zoals we al eerder de warmtecapaciteit berekenden voor een voorwerp dat voor een deel uit aluminium en voor een deel uit koper bestaat.
Voor de calorimeter weten we dat al: 209 J/K . Voor de 500 g water is dat 0,5 x 4180 = 2090 J/K .
Onze calorimeter met water heeft dus een totale (voorwerps)warmtecapaciteit van 2 090 + 209 = 2299 J/K
Nu calorimeter en 500 g water zijn samengevoegd beschouwen we die als één "stof":
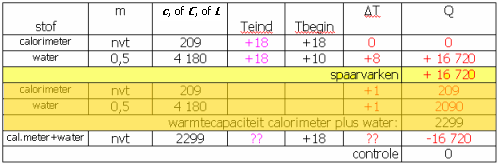 (afb 10)
(afb 10)Nu kun je de laatste regel doorrekenen via een ΔT van -7,27 K naar een eindtemperatuur van +10,73°C.
6: Fase-overgangen in de rekentabel
6.1 Water en stoom: verdampen en condenseren, eindtemperatuur gevraagd
Bij koken van water ontstaat stoom. Je blijft energie toevoeren aan je pan op het fornuis, maar het water wordt niet warmer dan 100°C terwijl het water in stoom van 100°C verandert. De temperatuur verandert niet, alle energie wordt dan gebruikt om de watermoleculen uit de vloeistof los te maken tot losse gasmoleculen.
Dat noemen we ook wel latente warmte
(latent = onzichtbaar aanwezig, je kunt die extra energie niet meten met bijv. een thermometer)
Waterdamp (stoom is waterdamp met een temperatuur boven het kookpunt van water) is een andere stof dan water, en heeft zijn eigen soortelijke warmtecapaciteit. Die is voor waterdamp van atmosferische druk 2027 J/kg·K.
( !! cwaterdamp is sterk afhankelijk van de druk, maar dat laten we in deze cursus buiten beschouwing)
We weten nu genoeg voor de volgende opgave:
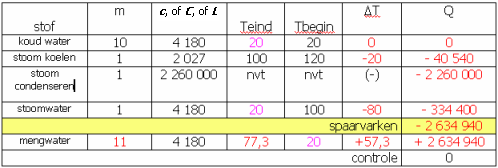
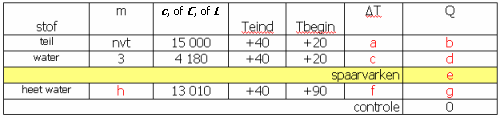
"Met 1 kg oververhitte stoom van 120°C en 1 bar wordt 10 kg water van 20°C opgewarmd. Wat is het eindresultaat?"
We gaan dit weer oplossen met de tabelmethode. <table cellpadding="0" cellspacing ="0" border="0" class="bbc">[tr][td] Denk aan onze eerder geconstateerde overeenkomsten tussen de diverse formules. Als we een regel gebruiken voor latente warmte L is er geen ΔT, en dus ook geen Tbegin of Teind.
Wat we wél doen:
- Bij ΔT vullen we als denkhulpje een (+) of (-) in: bijvoorbeeld bij smelten van ijs zal de temperatuur toenemen als je het bekijkt van vlak vóór tot vlak ná het smelten, gebruik dus een (+). Denk aan een T/Q-grafiek als hiernaast:
Zo zie je, consequent werken en alles blijft kloppen. [/td][td]
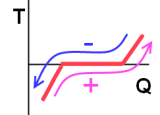 (afb. 11) [/td][/tr]</table></div>
(afb. 11) [/td][/tr]</table></div>Dan kunnen we nu onze rekentabel gaan maken.
Om te beginnen bepalen we hoeveel "verschillende stoffen" er in je opgave zitten. Een "stof" noemen we alles waarvoor je een aparte massa, óf soortelijke warmte, óf temperaturen, óf warmtestroom voor gegeven of gevraagd krijgt.
We hebben stoom en water. Dat zijn al twee "stoffen". De stoom moeten we gaan opdelen in drie "stoffen":
- stoom afkoelen (c = 2027 J/kg·K),
- stoom condenseren tot water (Lv = 2 226 000 J/kg),
- en ten slotte het gecondenseerde water afkoelen tot de evenwichtstemperatuur (c = 4180 J/kg·K).
- alle "beginstoffen" uiteindelijk laten afkoelen tot één Teind (bijv 20°C). (Voor stoom moet dat natuurlijk wel via 100°C)
- de "eindstof"regel, die dan natuurlijk voor Tbegin 20°C krijgt (de gekozen Teind van de stoom en het koude water).
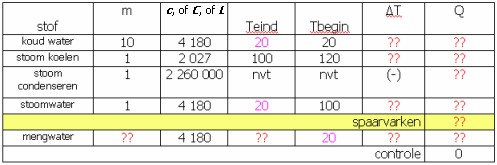 (afb. 12)
(afb. 12)Verborgen inhoud
moet je uitkomen op 11 kg water van 77,3°C6.2 Water en ijs: smelten en stollen
Dit is niet wezenlijk anders dan verdampen en condenseren: Het smeltpunt van water is 0°C. Alle energie wordt dan gebruikt om de watermoleculen uit het ijskristalrooster los te maken tot losse watermoleculen.
Ook hier verandert de temperatuur niet tijdens het smelten, we hebben dus te maken met latente warmte.
De soortelijke smeltwarmte van ijs is 334 000 J/kg. Heel wat minder dan die 2 260 000 J/kg voor verdamping van water, maar toch nog altijd veel meer dan de energie nodig om een kg water 1°C op te warmen. (4180 J/kg·K).
De stof ijs heeft zijn eigen soortelijke warmtecapaciteit: 2200 J/kg·K.
Dus daar hoeven we niet veel woorden meer aan vuil te maken. Een opgaafje dan maar.
"Aan 1 kg ijs van -5°C wordt 2 kg water van 50°C toegevoegd. Wat is het resultaat?"
Denk weer aan je stappenplan. Je hebt hier weer 4 beginstoffen: ijs opwarmen, ijs smelten en ijswater opwarmen, en water afkoelen. En een eindstof. Kies weer een handige eindtemperatuur van je beginstoffen (wij kiezen 0°C vloeistof)
en komen na het logisch afwerken van de stappen uit op 3 kg water van 5,8°C.
Probeer het zelf, en kijk dan maar in de
Verborgen inhoud
7: Andere tussenstappen
Als je zo nog eens door de voorgaande rekenvoorbeelden bladert valt op dat we steeds met één stof eindigden, en als tussenstap onze beginstoffen op één tussentemperatuur brachten. Maar de mogelijkheden om te variëren voor een vragensteller zijn natuurlijk bijna eindeloos. Er kan gevraagd worden naar de warmte, de begintemperatuur, de massa of de warmtecapaciteit van een van de "stoffen", en dat voor de gekste combinaties van "stoffen". Voor onze tabelstrategie maakt dat weinig uit: invullen wat we weten, en per regel en kolom kijken wat we kunnen uitrekenen. Maar je zou wel eens andere tussenstappen nodig kunnen hebben.
7.1 gevraagd: de massa van een van fase veranderende stof
"Welke massa ijs van -5°C moeten we toevoegen aan 1 kg water van 20°C om water van 2°C te krijgen?"
Wat we weten gaat eerst in de tabel: we kunnen echter niet gaan berekenen wat er gebeurt als we al onze beginstoffen eerst naar één gezamenlijke willekeurige tussentemperatuur brengen: we weten namelijk niet hoeveel beginstof we hebben. We moeten ons "spaarvarken" dus een tikje anders gaan gebruiken.
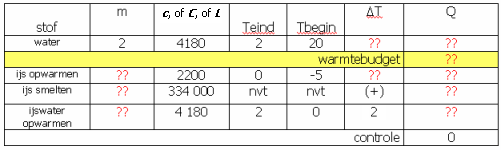 (afb. 15)
(afb. 15)Dan uitrekenen wat we kunnen:
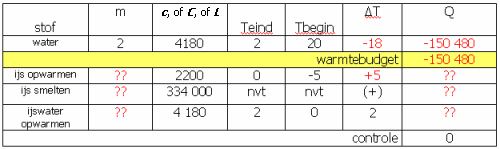 (afb. 16)
(afb. 16)Maar dan lopen we vast..... We hebben namelijk geen formules meer in onze tabel met maar één onbekende. In totaal moeten we nu + 150 480 J gaan verdelen over het opwarmen van het ijs, het smelten van het ijs en het opwarmen van dit ijswater. 3 onbekenden dus? Welnee. De massa is steeds dezelfde !
Een handige mogelijkheid voor een tussenstap: We gaan net doen alsof we 1 kg ijs gaan opwarmen, smelten en verder opwarmen, en eens kijken hoeveel energie dat allemaal voor die ene kilogram kost.
- ijs opwarmen: Q = m·c·ΔT = 1 x 2200 x 5 = 11 000 J
- ijs smelten: Q = m·c = 1 x 334 000 = 334 000 J
- ijswater opwarmen: Q = m·c·ΔT = 1 x 4180 x 2 = 8 360 J
 (afb. 17)
(afb. 17)dat is dus +353 360 J voor 1 kg. Dat kun je schrijven als +353 360 J/kg. Hierin zit dan de temperatuurverandering al verrekend, het heeft daardoor dezelfde eenheid als latente warmte, en dus kunnen we het invullen op een regel ijs totaal (ijs opwarmen, smelten en verder opwarmen tot 2°C). Omdat de temperatuursverandering al verrekend is zijn Tbegin en Teind niet meer van toepassing. Omdat de temperatuur stijgt bij dat proces vullen we bij ΔT ons denkhulpje (+) in.
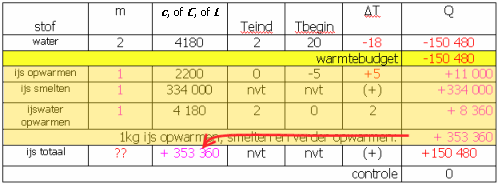 (afb. 18)
(afb. 18)Nu is het een koud kunstje om te berekenen dat er 150 480/353 360 = 0,426 kg ijs nodig was.
7.2 gevraagd: de eindtoestand (evenwichtstoestand) van een fase-mengsel
In de situaties die je tot nu toe zag eindigden we steeds met één (eind)stof. Maar als je bijvoorbeeld koud water toevoegt aan een portie onderkoeld ijs is de kans groot dat je eindigt met meer ijs dan waarmee je begon, en nog een restant water bovendien:
"Aan 2 kg ijs van -20°C wordt 1 kg water van +2°C toegevoegd. Wat tref je aan in het vat nadat evenwicht is opgetreden? (verwaarloos de warmtecapaciteit van het vat)"
Het is niet gegeven hoe dit eindigt, en dit soort gevallen zijn niet zo voorspelbaar, en dus ook niet in één stap af te werken. Alle gevallen waarvan je niet weet hoe het afloopt kun je het beste maar oplossen zoals je in het begin al leerde: breng als tussenstap je beginstoffen samen naar één toestand, hier bijvoorbeeld vloeibaar water van 0°C:
Kijk dan eens wat je aan energie overhoudt, of juist tekortkomt, m.a.w. de inhoud van je spaarvarken:
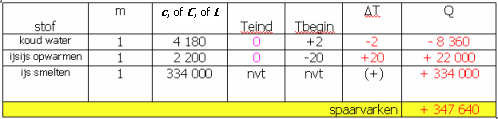 (afb. 19)
(afb. 19)Tja, nu hebben we 2 kg water van 0°C, maar daarvoor is er 347 640 J in het systeem gestopt. Er is maar één manier om dat terug te krijgen: water bevriezen tot ijs van 0°C:
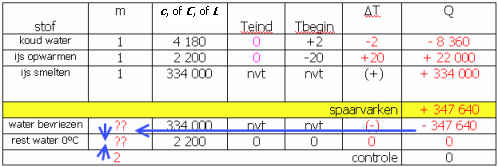 (afb. 20)
(afb. 20)Als je dit even doorrekent is met de vorming van 1041 g ijs de "uitgeleende" energie weer "terugbetaald". Als eindtoestand krijgen we dus 1041 g ijs en 959 g water, elk van 0°C.
Dit hadden we ietsje handiger kunnen oplossen. We zagen dat het afkoelen van het water 8 360 J opleverde, maar het opwarmen van het ijs tot ijs van 0°C al 22 000 J kostte. Toen al hadden we kunnen concluderen dat we per saldo water zouden moeten gaan bevriezen. Die kilogram ijs dus eerst nog te gaan smelten was een overbodige stap. Nooit erg, het eindresultaat is toch hetzelfde. Dat is overigens best belangrijk om te beseffen: ga niet teveel zitten piekeren. Het ergste wat je kan overkomen als je niet superhandig werkt is dat je wat extra rekenwerk krijgt.
7.3 Andere bronnen van warmte
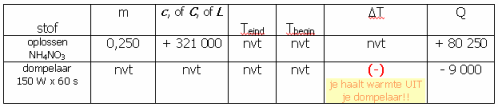
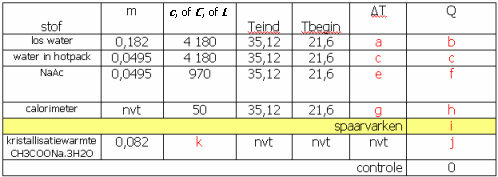
In een calorimeter kun je ook chemische reacties laten plaatsvinden. Die gaan bijna altijd met afgifte (exotherm, "exo"-de warmte komt eruit) of opname (endotherm, "endo"-de warmte gaat erin) van warmte gepaard. Voorbeelden hiervan zijn het oplossen of laten kristalliseren (kristallisatiewarmte) van zouten. Het oplossen van 1 kg ammoniumnitraat kost bijvoorbeeld ongeveer 321 000 J (oploswarmte= + 321 000 J/kg). Zoiets wordt dan nuttig gebruikt in coldpacks.
<table cellpadding="0" cellspacing ="0" border="0" class="bbc">[tr][td]Een ander voorbeeld is het opwarmen van de stof in je calorimeter met behulp van een elektrische verwarmingselement, een dompelaartje. De energie die zo'n ding levert bereken je met de formule:
\(E=P\times t\)
(bijv.: E= 150 W x 60 s = 9 000 J.) [/td][td]  (afb. 21)[/td][/tr]</table></div>
(afb. 21)[/td][/tr]</table></div>Dit soort zaken kun je zó in je tabel plaatsen:
 (afb. 22)
(afb. 22)Merk op dat er warmte UIT je dompelaar komt. Die warmte krijgt op de dompelaar-regel dus een (-) teken!!
8: Plagerijen van opdrachtenschrijvers.
Alle truuks heb je nou wel ongeveer gezien. We kunnen nog gaan vragen om wamtecapaciteiten of soortelijke warmtes te berekenen, maar dat is eigenlijk alleen maar meer van hetzelfde. Ingewikkelder kan het haast niet worden, wel uitgebreider, met meer stoffen, maar met je tabel hou je daarover wel het overzicht.
Er is nog maar één manier om het moeilijker te maken: de bruikbare gegevens nog een laag dieper verstoppen.
Er wordt bijvoorbeeld geen massa meer gegeven, maar wél een volume en een dichtheid van een stof. Tja, eerst maar even omrekenen dan, via een formuletje uit je tweede leerjaar: ρ= m/V.
Of voor het vermogen van een elektrische dompelaar krijg je geen gegeven in watt, maar wel een stroomsterkte en een spanning. Dat is een ander hoofdstuk uit je natuurkundeboek, P= U·I.
Of we geven er een hoopje overbodige gegevens bij, waaruit je zelf de nuttige maar moet zien te halen.
Hoe dan ook, dat heeft allemaal weinig meer met warmtecapaciteit te maken. Zorg dat je jezelf niet in de war laat brengen.
9 Ten slotte: kanttekeningen
In heel de natuurkunde is er vrijwel overal een verschil(letje) tussen theorie en praktijk. Zo leer je dat vloeistoffen niet samendrukbaar zijn: nou, dat zijn ze wel, een heel klein beetje. Of de algemene gaswet: die geldt voor ideale gassen, en ideale gassen bestaan niet. Maar meestal doen we net alsof, omdat de verschillen in de praktijk meestal verwaarloosbaar klein zijn.
Zo ook hier. We werken met getallen uit tabellenboeken voor de soortelijke warmte van stoffen, en doen net of die bij alle temperaturen gelijk zijn. De praktijk is helaas net een tikje anders. Tussen 0°C en 100°C varieert de soortelijke warmte van water met ongeveer 1%, met bijna gelijke maxima bij 0 en 100°C en een minimum bij 35°C. Om water op te warmen van 14,5°C naar 15,5°C kost 4185,5 J/kg. Dat wordt ook wel de c15 genoemd. Andere stoffen gedragen zich weer anders. Ook verandert de soortelijke warmte een beetje (en voor gassen zelfs heel sterk) als druk of volume veranderen. Voor stoom zie bijvoorbeeld: http://www.thermexcel.com/english/tables/vap_eau.htm
Bij gassen scheelt het qua soortelijke warmte ook nogal of je de proeven uitvoert bij een gelijkblijvende druk (cp) of bij gelijkblijvend volume (cv) tijdens de temperatuursveranderingen. Het begrip enthalpie komt dan om de hoek kijken.
Behalve smelten, stollen, verdampen en condenseren zijn er nog de fase-overgangen direct van vaste stof naar gas (sublimeren) en van gas terug naar vaste stof (rijpen). Deze zul je in dit soort opgaven zelden tegenkomen. Er is trouwens weinig bijzonders aan de hand: bijvoorbeeld voor sublimatiewarmte van ijs tel je gewoon de smeltwarmte van ijs en de verdampingswarmte van water bij elkaar op. Dat volgt per definitie uit de wet van behoud van energie, met slechts kleine foutjes omdat ook latente warmte in tabellenboeken meestal alleen zijn gegeven bij de "normale" smelt- en kookpunten.
Bijlage: Grootheden, eenheden, definities, formules
grootheid: MASSA ( m )
definitie: de hoeveelheid van een stof
SI-eenheid: kilogram (kg)
grootheid: TEMPERATUUR ( T )
definitie: een maat voor de bewegingsenergie van deeltjes in een hoeveelheid stof
SI-eenheid: kelvin (K) (we zullen hier overigens vaak met graden Celcius (°C) werken)
De eenheid K is overigens even groot als de eenheid °C. Alleen het nulpunt ligt anders:
0 K is dus - 273°C (eigenlijk -273,15°C, maar dat is niet zo belangrijk)
Nou zullen we in deze cursus vaak rekenen met verandering van temperatuur (ΔT) , (spreek uit: delta T). Omdat 1 K even groot is als 1°C maakt het dan weinig meer uit of we kelvin of graden Celsius gebruiken. Een ΔT van 21 K is een precies even grote verandering als een ΔT van 21°C. ](*,)
temperatuurverandering is eindtemperatuur minus begintemperatuur
\(\Delta T = T_{eind} - T_{begin}\)
grootheid: WARMTE ( Q )
definitie: Warmte is de energie die als gevolg van een temperatuurverschil door een warmtegeleidende wand stroomt. Warmte is een moeilijk begrip. (VERWAR HET NIET MET TEMPERATUUR!!) Warmte is een energiestroom. Je kunt dus niet spreken over 'de warmte' van een hoeveelheid stof. Geen paniek, je zult zien dat dit in de praktijk veel simpeler is dan het lijkt.
SI-eenheid: joule (J) (niet toevallig dezelfde als van energie)
grootheid: (voorwerps)WARMTECAPACITEIT ( C )
definitie: de hoeveelheid energie in joule die nodig is om een voorwerp één kelvin in temperatuur te laten stijgen. Deze is natuurlijk alleen voor precies dezelfde voorwerpen gelijk. Een groter voorwerp zal een grotere warmtecapaciteit hebben.
SI-eenheid: joule per kelvin (J/K) (de massa (kg) staat niet in deze formule: hij is vastgesteld voor het voorwerp, de massa is daar al in verrekend)
Warmte is de (voorwerps-) warmtecapaciteit maal de temperatuurverandering
\(Q= C \cdot \Delta T\)
grootheid: SOORTELIJKE WARMTECAPACITEIT ( c )
definitie: de hoeveelheid energie in joule die nodig is om één kilogram van een stof één kelvin in temperatuur te laten stijgen. Deze is voor alle stoffen verschillend. Je kunt het voor de meeste stoffen in een tabellenboek vinden.
SI-eenheid: joule per kilogram per kelvin (J/kg·K) :
Warmte is de massa maal de (soortelijke) warmtecapaciteit maal de temperatuurverandering
\(Q=m \cdot c \cdot \Delta T\)
FASE: de toestand waarin een stof zich bevindt.
In deze cursus beperken we ons tot de drie belangrijkste fasen: vaste stof, vloeistof, gas (damp)
grootheid: LATENTE WARMTE ( L... ) (smelt-, stollings-, verdampings- en condensatiewarmte.)
definitie: de hoeveelheid energie in joule die nodig is (of die vrijkomt) bij het veranderen van de fase van een kilogram van een stof (bij gelijkblijvende temperatuur)dus bijvoorbeeld de warmte die nodig is om een kg ijs te laten smelten bij 0°C, of juist de warmte die vrijkomt als een kg water een kg ijs wordt.
SI-eenheid: joule per kilogram (J/kg) (de temperatuur (K) staat niet in deze formule: die verandert niet bij een fase-overgang: verdampen - condenseren - smelten - stollen)
Warmte is de massa maal de (soortelijke) fase-overgangswarmtecapaciteit
\(Q=m \cdot L_{...}\)
1) Als er tussen twee stoffen een temperatuurverschil bestaat, ontstaat er een warmtestroom totdat beide stoffen een gelijke temperatuur hebben.
2) De energie die de ene stof daarbij afstaat is gelijk aan de energie die de andere stof opneemt.
De som van alle warmtestromen is nul.
\(Q_1 + Q_2 + Q_3 + {.......} = 0\)
plus: de stof ontvangt energie. (of snelheid, of massa, of wat ook)
min: de stof staat energie af. (of snelheid, of massa of wat ook)
 (afb. 13)
(afb. 13)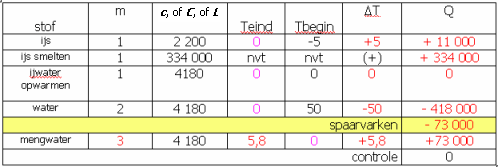 (afb. 14)
(afb. 14)
 (afb. 1)
(afb. 1) 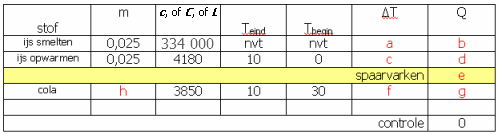 (afb. 2)
(afb. 2) 

 (afb. 3)
(afb. 3) 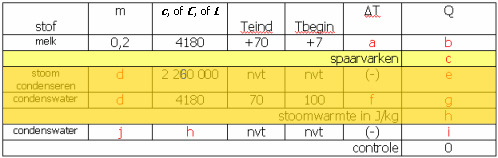 (afb. 4)
(afb. 4) 

 (afb. 5)
(afb. 5) 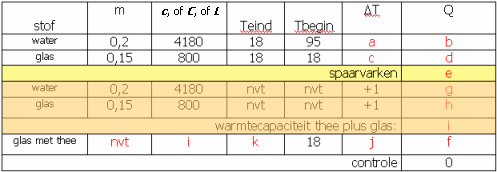 (afb. 6)
(afb. 6) 