In het huiswerkforum vind je een topic voor je vragen en opmerkingen over de cursus en/of de oefenopgaven.
Zit je met een opgave over krachten waar je niet aan uit geraakt? Open dan een topic in het huiswerkforum.
Er is ook een volledig overzicht van alle cursussen, FAQ's en handleidingen
Oefenopgaven
Inleiding oefenopgaven
Je kunt deze oefenopgaven allemaal óf grafisch óf met een berekening oplossen.
Maak in alle gevallen een schets. Voor een grafische oplossing zal die zo netjes mogelijk moeten zijn, voor een berekening is een ruwe schets meestal wel voldoende. Voor grafische oplossingen: maak je schetsen groter dan wij hier doen, anders meet je al snel onnauwkeurig.
Het (kale) eindantwoord en de uitwerking vind je steeds door te klikken op de respectievelijke
Verborgen inhoud
uitwerking.....
Grafisch zul je nooit zó nauwkeurig zijn. Wijkt je antwoord niet meer dan 5% af van het berekende antwoord, dan heb je netjes gewerkt.
Let in de berekende antwoorden niet op de significantie van de cijfers. Gezien de bedoeling van de oefeningen geven we het antwoord steeds afgerond op hele newtons of graden.
1 Luchtweerstand
De motor van een auto levert een kracht van 1000 N vooruit. Bij een snelheid van 30 m/s is de luchtweerstand 800 N, en de rolwrijving van de wielen samen 100 N.
a) Hoe groot is de nettokracht op de auto?
antwoord:
Verborgen inhoud
100 N vóóruit
uitwerking:
Verborgen inhoudGrafisch:
Goeie richtingen geven, en op juiste schaal tekenen. Dan nog eens, maar met de één voor één methode, steeds een opschuiven en met de voet op de punt van de vorige plakken. In dit geval zul je misschien die moeite niet eens doen omdat je het zo wel ziet, toch?
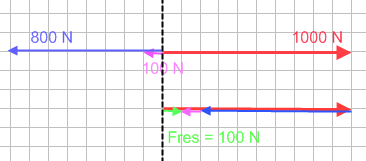 (Afb.38)
(Afb.38)
Berekenen:
Let op de tekens van je getallen: de ene kant op plus, de andere kant op consequent min.
Fres = +1000 N + (-800 N) + (-100 N) = +100 N
b) Extraatje, buiten het doel van deze cursus, maar toch leuk: Stel de rolwrijving was niet 100 maar 200 N geweest. De nettokracht op de auto wordt dus 0 N (reken maar na). Welke bewering is dan juist?
<ul class="bbcol">[*]De auto zal even later sneller rijden.
[*]De auto zal zo snel blijven rijden.
[*]De auto zal vertragen.
[*]Dan klopt deze opgave niet. Als de nettokracht 0 N is kan het niet anders of de auto staat stil.
[/list]
antwoord:
Verborgen inhoud
B
uitwerking:
Verborgen inhoud
De nettokracht is nu 0 N. Dat betekent dat er niets verandert aan de beweging van de auto. Als hij stilstond blijft hij stilstaan, als hij rijdt blijft hij even snel rijden. Als je antwoord D gaf moet je nodig terug naar je docent om extra uitleg over het effect van krachten, want dan heb je iets niet goed begrepen.
2 De trekschuit
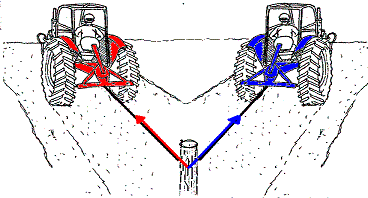
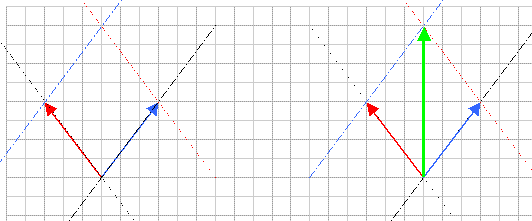
Een trekschuit wordt door twee paarden voortgetrokken over een rivier. Vlak voor een bocht trekken de paarden met krachten in richtingen zoals in de afbeelding. De hoek tussen het blauwe touw en de vaarrichting van de schuit is 19°. De hoek tussen de touwen van de paarden is 90°.
Bepaal de grootte van de resulterende kracht van de twee paarden op de trekschuit.
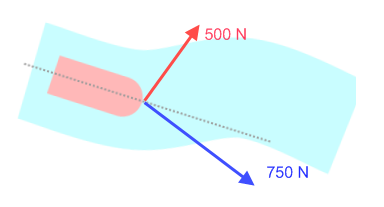 (Afb.39)
(Afb.39)
antwoord:
Verborgen inhoud
901 N
uitwerking:
Verborgen inhoudGrafisch:
de krachten zijn al voor je getekend. Teken ze anders netjes zonder schuit e.d. haaks op elkaar op een ruitjespapier. Schaal is hier 1 cm = 200 N. Teken een parallellogram met de bekende krachten aan twee zijden. De resulterende kracht heeft nu zijn voet op de schuit, en zijn punt in de tegenoverliggende hoek van het parallellogram. Opmeten levert 4,5 cm ofwel op deze schaal 900 N.
Trek je dus niks aan van de vaarrichting van de schuit. Er wordt niet gevraagd om de nettokracht in de vaarrichting!!
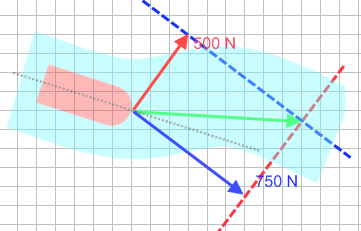 (Afb.40)
(Afb.40)
Berekenen:
Gegegeven is de hoek tussen de twee krachten van 90°. Het parallellogram is dus een rechthoek. In dat geval kun je moeiteloos Pythagoras toepassen.
Fres²= 500² +750²
Fres = √(500² +750²) = 901 N
3 Jaap trekt een kar
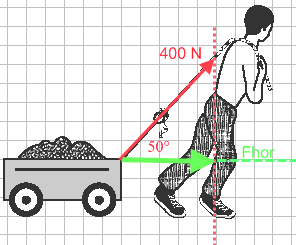
Jaap trekt met een touw aan een karretje met zand. Via het touw oefent hij een kracht uit van 400 N. Het touw hangt over zijn schouder en maakt een hoek van 50° met de rijrichting van het karretje. Hoe groot is de resulterende kracht in horizontale richting (F
hor) van Jaap in de rijrichting van het karretje?
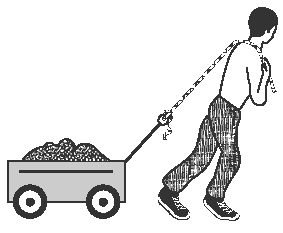 (Afb.41)
(Afb.41)
antwoord:
Verborgen inhoud
257 N
uitwerking:
Verborgen inhoudGrafisch:
de kracht is 400 N, teken die over het touw, met de voet van de pijl op het punt waar het touw aan de kar vastzit. Een handige schaal is 1 cm = 100 N. Teken dan een stippellijn in de rijrichting van het karretje, en een loodlijn vanaf de punt van je pijl naar die rijrichtingslijn. Je kunt nu de resulterende Fhor tekenen en opmeten. Fhor ≈ 2,5 cm ofwel 250 N.
 (Afb.42)
(Afb.42)
Berekenen:
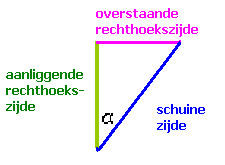
In de rechthoekige driehoek in je schets ken je de hoek van 50°, de lengte van de schuine zijde (400 N) en de aanliggende rechthoekszijde Fhor wordt gevraagd. Het is hier dus handig de cosinus van 50° te gebruiken (cos = aanliggende rechthoekszijde / schuine zijde)
cos(50°) = Fhor/400 N
Fhor = cos(50°) x 400 N = 0,6428 x 400 N = 257 N
4 De torenklok
Het dak van een kerktoren wordt gesteund door twee spanten, die een hoek van 30° met elkaar maken. Aan de nok wordt met een ketting een grote klok opgehangen, met een gewicht van 10 000 N. Hoe groot is de kracht die dat in de langsrichting van elk dakspant veroorzaakt?
antwoord:
Verborgen inhoud
5 176 N
uitwerking:
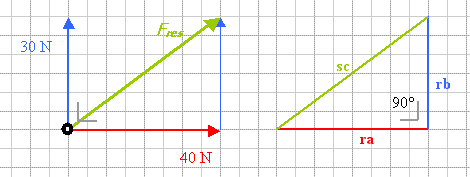
Verborgen inhoudGrafisch:
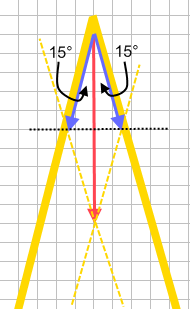
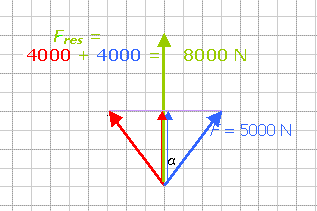
Twee bruine dakspanten met daartussen een hoek van 30°. Verticaal vanuit de nok hangt een klok, de zwartekracht op de klok is 10 000 N. Ontbind deze kracht mbv de parallellogrammethode in twee krachten in de richtingen van de spanten (want dat is de enige weg om die krachten weg te leiden naar de muren en zo verder naar de grond). Netjes opmeten levert ongeveer 5200 N per spant.
 (Afb.43)
(Afb.43)
Berekenen:
In je schets zie je rechthoekige driehoeken, met een tophoek van 15°, en een aanliggende rechthoekszijde van 5000 N. De schuine zijde is waarnaar je op zoek bent.
cos(15°) = 5000 N / schuine zijde
Fspant = 5000 N / cos(15°) = 5000/0,9659 N = 5 167 N
5 De vrachtwagenmotor in de garage
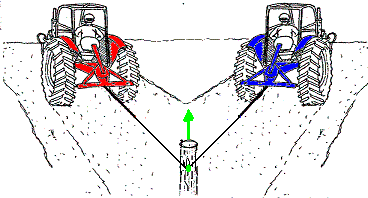
Het dak van een garage wordt gesteund door twee spanten, die een hoek van 160° met elkaar maken. Aan de nok wordt met een takel een vrachtwagenmotorblok met een gewicht van 10 000 N uit het chassis getakeld. Hoe groot is de kracht die dat in de langsrichting van elk dakspant veroorzaakt?
antwoord:
Verborgen inhoud
28 794 N
uitwerking:
Verborgen inhoudEigenlijk gelijk aan de kerktoren van vraag 4, maar toch een spannend verschil:
Grafisch:
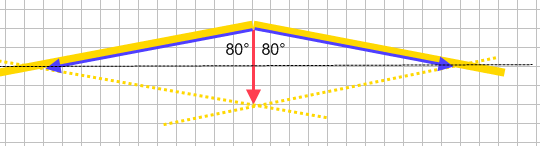
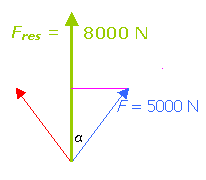
Als je dit doet met dezelfde schaal als de kerktoren, dan kom je er straks achter dat je papier niet breed genoeg is. Wij gebruiken hier de schaal 1 cm = 5000 N. Twee bruine dakspanten met daartussen een hoek van 160°. Verticaal vanuit de nok hangt het motorblok, de zwaartekracht op de motorblok is 10 000 N. Ontbind deze kracht mbv de parallellogrammethode in twee krachten in de richtingen van de spanten (want dat is de enige weg om die krachten weg te leiden naar de muren en zo verder naar de grond). Netjes opmeten levert ongeveer 29 000 N  per spant. Toch is het motorblok maar even zwaar als de kerkklok!
per spant. Toch is het motorblok maar even zwaar als de kerkklok!
 (Afb.44)
(Afb.44)
Berekenen:
In je schets zie je rechthoekige driehoeken, met een tophoek van 80°, en een aanliggende rechthoekszijde van 5000 N. De schuine zijde is waarnaar je op zoek bent.
cos(80°) = 5000 N / schuine zijde
Fspant = 5000 N / cos(80°) = 5000/0,1736 N =28 794 N
Dat is véél meer dan de krachten in de spanten bij de kerktoren, precies omdat het dak véél vlakker is. Als je vlakke daken construeert is dat een factor om heel goed rekening mee te houden.
6 Drie honden vechten om een been
Eén grote en twee wat kleinere honden hebben samen één bot vast, en trekken eraan met onderlinge hoeken van 120°. De grote hond trekt met een kracht van 60 N, de beide andere elk met een kracht van 40 N. Met welke nettokracht wordt het bot welke kant op getrokken?
antwoord:
Verborgen inhoud
netto 20 N in de richting van de grote hond.
uitwerking:
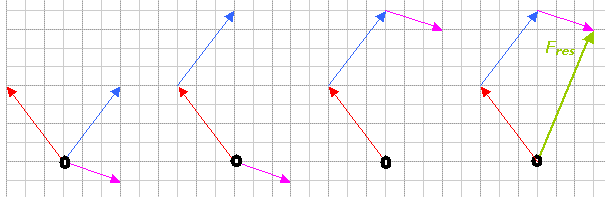
Verborgen inhoudGrafisch:
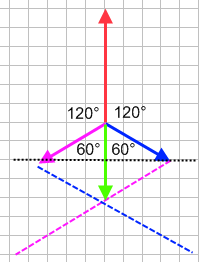
Eerst de drie krachten tekenen met een gezamenlijk aangrijpingspunt (het bot). De twee kleine krachten zijn makkelijk met de parallellogrammethode samen te stellen tot één gezamenlijke, die óók 40 N blijkt te zijn. Die werkt precies tegengesteld aan de 60 N van de grote hond. Als je dán die twee krachten samenstelt blijft er een nettokracht van 20 N in de richting van de grote hond over.
 (Afb.45)
(Afb.45)
Berekenen:
In je schets zie je rechthoekige driehoeken, met een tophoek van 60°, en een schuine zijde van 40 N. De aanliggende rechthoekszijde is waarnaar je op zoek bent, voor élk hondje.
cos(60°) = aanliggende rechthoekszijde / 40 N
Fres = 40 N x cos(60°) = 40 N x 0,5 =20 N
Dat geeft je de kracht van één hondje in de samengestelde richting. De resultante van de twee hondjes samen in hun gezamenlijke richting tegen de grote hond in is dus 40 N. De rest verspillen ze aan onderling "getouwtrek" in horizontale richting. De uiteindelijke resultante van álle krachten wordt dan +60 N +(-40 N)= +20 N
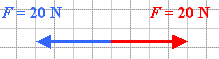
 (Afb.1)..............een kracht heeft een GROOTTE..............
(Afb.1)..............een kracht heeft een GROOTTE.............. (Afb.2)
(Afb.2)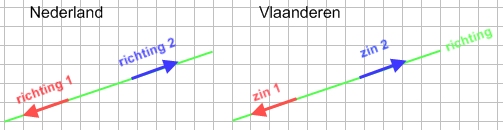 (Afb.2a)
(Afb.2a)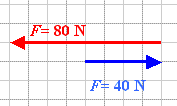 (Afb.3)
(Afb.3)
 ........
........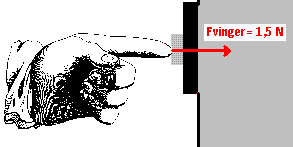 (Afb.4)
(Afb.4)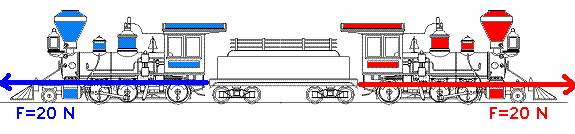





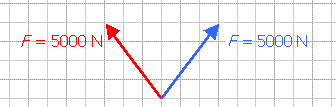
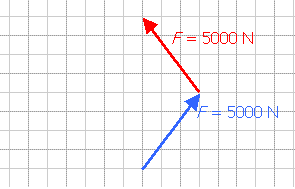
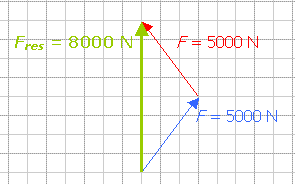
 (Afb.21a)
(Afb.21a)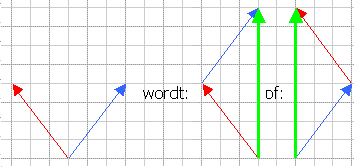




 (Afb.29)
(Afb.29)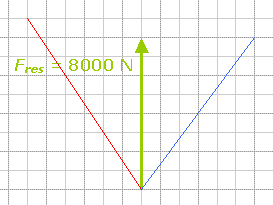 (Afb.30)
(Afb.30)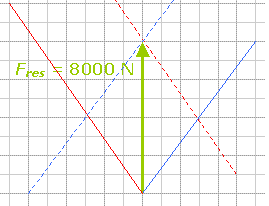 (Afb.31)
(Afb.31)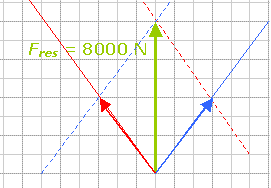 (Afb.32)
(Afb.32)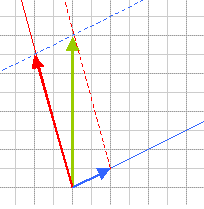 (Afb.33)
(Afb.33)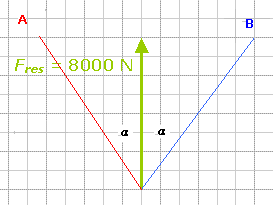 (Afb.34)
(Afb.34)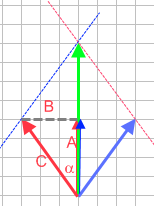 (Afb.35)
(Afb.35)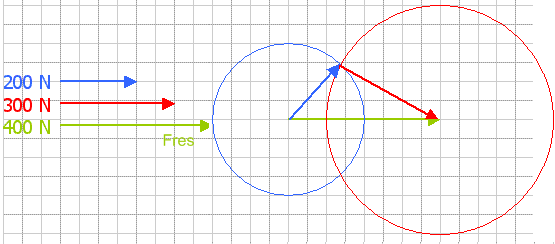 (Afb.36)
(Afb.36)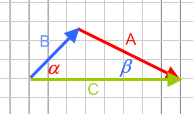 (Afb.37)
(Afb.37)

 (Afb.38)
(Afb.38) (Afb.39)
(Afb.39) (Afb.40)
(Afb.40) (Afb.41)
(Afb.41) (Afb.42)
(Afb.42) (Afb.43)
(Afb.43) (Afb.44)
(Afb.44) (Afb.45)
(Afb.45)